气动伺服弹性对导弹飞行状态的影响研究*

李培垚，李文光，刘 莉，周 玙

(北京理工大学，北京 100081)

0 引言

随着现代军事技术的不断发展，新材料、新技术在武器中的应用越来越广泛，无人机、飞机等作战目标的机动性越来越强，这对导弹的性能提出更高要求，为提高导弹的有效载荷，在设计导弹时，导弹的结构质量也在不断减小，因此科研人员在设计导弹时倾向于一种长度更长、弹径更小、壳体更薄的设计方案。但这种设计带来的气动弹性问题越来越明显。气动弹性是指非定常气动力与导弹结构弹性之间的动力耦合，在飞控系统带宽设计边界不断放宽的条件下，导弹气动伺服弹性不稳定现象发生概率变大，这种不稳定现象主要体现在对飞行稳定性与操纵性等方面。导弹在飞控系统的作用下，弹上敏感装置将测量到的弹性振动信息混入姿态角信息中，并将这些混合信息反馈给控制系统，使控制系统输出误差控制指令并操纵舵机偏转，从而改变导弹的气动力分布，而导弹姿态的改变又会带来非定常气动力，这种非定常气动力又会激励导弹结构弹性变形发生变化，由此可见，非定常气动力与结构弹性以及控制系统之间会发生耦合作用。

气动伺服弹性问题会影响导弹开环扰动频率特性，恶化导弹的动态品质。这主要是因为弹上的敏感元件使导弹动力学与控制系统发生闭环耦合，当导弹飞行速度达到临界值后，舵机负载的高频振荡可能会导致操纵面颤振，更严重时会发生弹体折断，这对导弹控制是极为不利的，因此在现代大长径比导弹的设计中，以往的刚体设计控制器不合时宜，需要考虑气动弹性的影响。国内外学者对此展开研究，提出不同的建模方法并进行分析[1]。樊则文[2]对导弹气动伺服弹性作了深入研究，杨超[3]等分析了带有舵面及控制系统的战术导弹气动伺服弹性稳定性，但在可控舵面只考虑刚体偏转。通过对已有的文献研究发现，大部分文献在建模方式上采用的是刚柔解耦的方法，并没有系统的分析方法。因此文中在充分考虑动态耦合的情况下，以某型导弹为研究对象，在综合考虑导弹刚体模态和弹性体模态的基础上，对导弹气动伺服弹性对导弹飞行状态的影响进行分析。

1 动力学模型

在研究导弹气动弹性问题时，常将导弹简化为梁模型，结合梁的弯曲振动理论，从刚性弹体受力分析出发，分析弹体发生弹性变形后受力情况发生的变化，并将这些变化完善到新的动力学模型中。文中采用的惯性坐标系、弹体坐标系、速度坐标系均与文献[4]中的定义一致，在此仅给出描述弹体变形量的弹性坐标系，定义其原点O位于导弹头部，Oxs轴与弹体纵轴重合，指向尾部为正，Oys轴位于导弹纵向对称面内，垂直于Oxs轴，Ozs轴由右手定则确定，如图1所示。

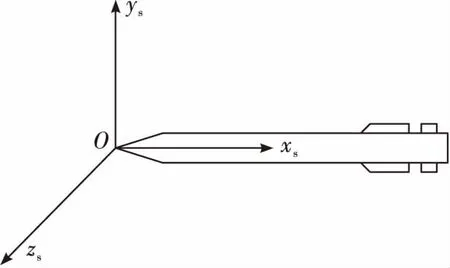
图1 弹性参考系

导弹动力学方程建立的方法有多种，通常在研究刚体导弹时，采用牛顿第二定律或达朗贝尔原理就可以方便地建立导弹的飞行动力学方程。但对于考虑弹体弹性的导弹，由于导弹内部的质量和弹性分布较为复杂，采用矢量平衡的方法建立方程较为困难，而应用包含能量的标量来建立方程更为方便。因此文中将采用速度变分原理，结合有限元方法，在结构动力学框架下，建立弹性体导弹的动力学方程：

(1)

式中：M、fin、fex、fde分别称为广义质量矩阵、广义惯性力阵、广义外力阵和广义变形力阵；v表示广义速度，包括导弹的质心运动速度，导弹的旋转角速度和模态速度。可分别表示如下：

(2)

(3)

(4)

(5)

(6)

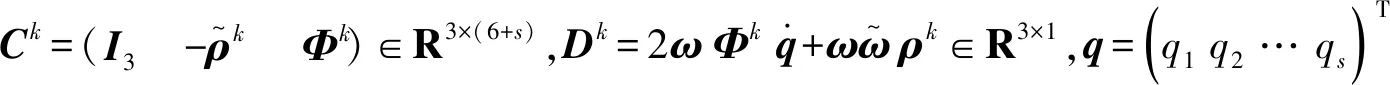
导弹所受的外力包括空气动力、推力、重力。可以表示为:

fex=fae+ft+fg

(7)

导弹受到的广义重力为：

(8)

式中：

(9)

导弹受到的广义推力可以表示为：

(10)

式中:

(11)

式中:

(12)

式中：下标t表示导弹推力作用点处相对应的量，Pt表示发动机推力。

导弹所受到的广义空气动力可以表示为：

(13)

式中:

(14)

若不考虑由于弹性振动引起的非定常气动力，此时，式(14)中:

(15)

(16)

以上两式中，S为导弹的参考面积，b为导弹的参考长度，cA表示轴向力系数，cN表示法向力，cZ表示侧向力系数，mxb、myb、mzb分别表示弹体坐标系3个坐标轴方向的力矩系数。气动系数cA、cN、cZ、mxb、myb、mzb是攻角α、侧滑角β、马赫数Ma和控制舵偏角δz的函数，可通过气动参数表插值(Datcom软件)计算得到，动压Q、攻角α和侧滑角β的计算与参考文献[1]中的计算方式一致，其计算公式如下：

(17)

(18)

(19)

式中：ρa为导弹所处高度空气密度；Vm为气流相对于导弹的流速，其矢量表示为：

Vm=V-Vw

(20)

式中:V表示导弹的绝对速度矢量;Vw表示阵风速度矢量，其矩阵表示形式为：

(21)

由以上推导得到气流相对于导弹的流速为：

(22)

上述推导过程是假设导弹在飞行过程中受到的空气动力与模态变量无关的定常气动力。事实上，由于弹性振动的存在，导弹存在正常攻角和侧滑角的情况下，也会引起附加攻角和侧滑角，这就使导弹产生附加的气动力和气动力矩，也就是文中要研究的气动弹性问题。

大长径比导弹受到的非定常气动力可以按照细长体理论进行计算[5]：

(23)

式中：ma表示单位长度上等体积的气体质量，va表示气体在该方向上的流动速度，其具体表达式为：

ma=ρas(x)

(24)

(25)

式中：s(x)为导弹横截面积，u(x,t)为导弹的弹性变形位移量。运用变量分离法，将弹性位移变形量分别对时间和位置求导，将式(24)和式(25)代入式(23)中可得：

(26)

由于弹性变形会造成附加攻角和侧滑角，因此在操纵舵面和弹翼上，弹性变形产生的附加攻角和侧滑角的表达式如下：

(27)

(28)

将附加气动力表示为列阵形式：

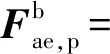
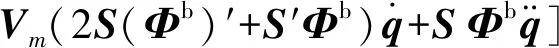
(29)

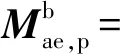
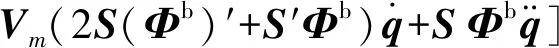
(30)

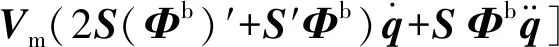
(31)

(32)

(33)

故而在考虑气动弹性的情况下，前述推导的广义气动力可以表示为：

(34)

式中：(Φ(w))T表示弹翼所处位置的模态振型平动分量的转置；(Φ(p))T表示舵面所处位置的模态振型的平动分量的转置。

与此同时，弹性变形对推力的作用也会有影响，推力始终沿着纵轴方向，但是当弹体由于横向振动发生变形时，推力不再沿着纵轴方向，此时推力会产生横向分量，以弹体坐标系y向为例，具体表现是，横向振动使得推力作用点和作用线发生变化，根据模态分析法得到推力作用点的y向位移为：

(35)

式中：xr为推力作用点处的坐标，其余变量定义与前述一致。考虑到对振型变量求导得到推力作用点处的转动角位移是一个小量，对附加推力计算几乎不起作用，故在此略去。同理对弹体坐标系z轴方向进行分析，化简得到：

(36)

从式(34)可以看出，推力附加项产生的本质是在弹体发生弹性变形后，推力在垂直于纵轴方向产生的投影量，将附加的推力项对质心取力矩，可得推力附加引起的附加力矩：

(37)

综上可得到考虑气动弹性的弹性体导弹动力学方程为：

(38)

式中:κ1～κ5、Κ1～Κ5均为常值转换矩阵，为了简化仿真流程，解决仿真计算量大的缺陷而使用，由于篇幅原因，这里不详细叙述。为与刚体导弹作对比，给出刚体导弹动力学方程：

(39)

2 控制方法

导弹在空气中飞行时，其控制力是由空气舵偏转产生的。所以控制方程的不同，导弹的弹道也就不同。文中内回路采用过载自动驾驶仪，初始阶段为无控阶段，其后选用比例导引进行制导。算例选取与目标的运动特性有关，为突出研究目的，对目标运动规律进行简化处理，只考虑目标质心的运动，目标运动方程如下：

(40)

过载自动驾驶仪的结构图如图2所示，由加速度主反馈回路和角速度阻尼回路构成。

图2 自动驾驶仪结构

导弹的导引方程为[6]：

(41)

式中:ac表示输入指令，ay表示导弹的法向加速度。当采用比例导引法时，输入指令具体形式为：

(42)

式中:σ表示目标视线角，且有

(43)

则目标视线旋转角速度可表示为：

(44)

此时导弹的飞行速度可以表示为：

(45)

目标的运动速度可以表示为：

(46)

导弹的弹道倾角可以表示为：

(47)

考虑到弹性振动对于测量信号的影响，控制器收到的控制信号中夹杂了包括弹性振动引起的干扰量，因此对前述自动驾驶仪的输入信号加以修正得到：

(48)

(49)

式中:Φb,py为敏感元件安装位置在y方向的振型。综上所述，考虑弹性影响的导弹导引方程应为如下形式：

(50)

3 仿真设计

3.1 算例

本部分首先利用MSC.Patran建立导弹的有限元模型，由于导弹为细长体，导弹的模型可以简化为变截面梁模型，经有限元计算，导弹的前三阶频率依次为12.9 Hz、33.8 Hz、57.6 Hz，并得到导弹的缩放模态振型向量，在弹体纵向对称面内对应的模态振型图如图3所示。

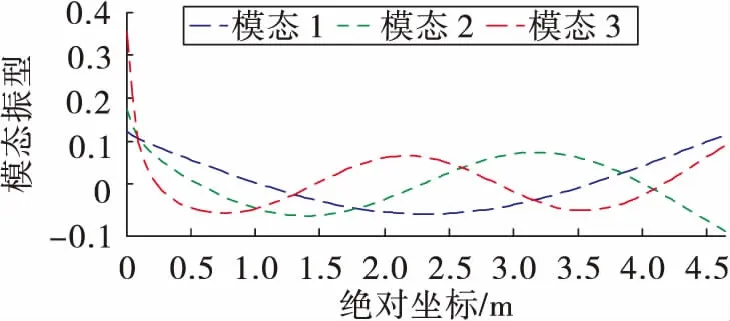
图3 前三阶弯曲模态振型图

利用Matlab编制仿真程序，求解上述动力学方程，完成对考虑气动弹性的弹性体导弹动力学模型和刚体导弹动力学模型的求解，程序中包括了导弹的两种动力学模型、目标的运动方程、控制方程、初始数据和数值积分方法，本算例采用的数值积分方法是四阶龙格库塔法，选取积分步长时，保证计算积分不出现发散的情况。本算例中，导弹初始发射角为30°，初始速度为20 m/s，其他初始条件均假设为0。目标以初始速度200 m/s在2 000 m高空运动，由图3分析假设弹上的敏感元件在弹身中部位置。导弹的基本参数如表1所示。

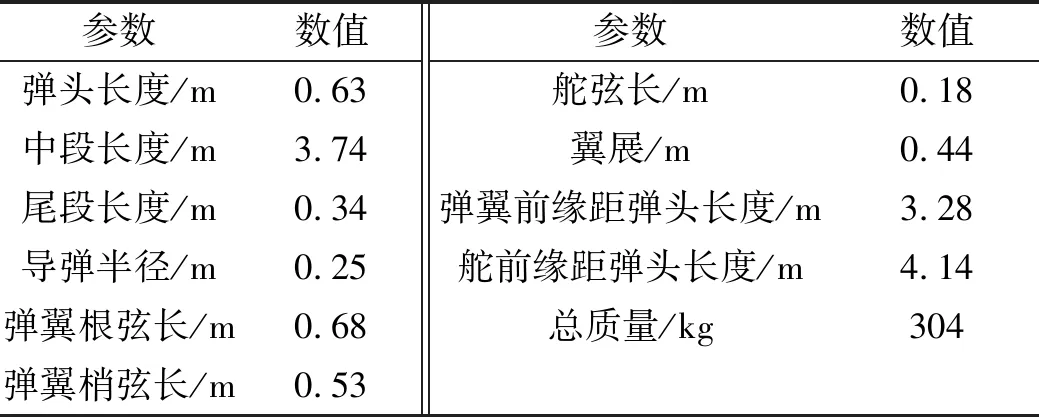
表1 某地空导弹的基本参数

3.2 仿真流程

文中设计的仿真程序流程如图4所示。

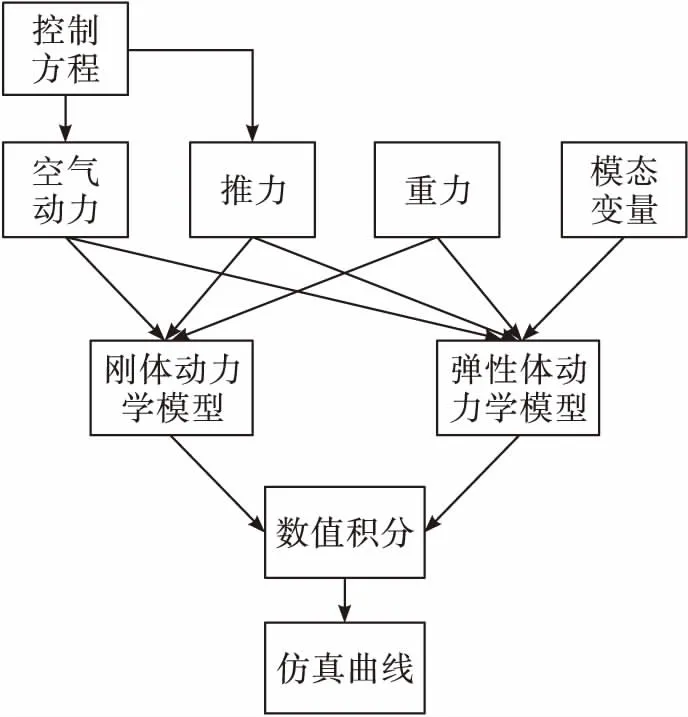
图4 仿真程序流程

作为比对，先对刚性导弹进行仿真，得到导弹的运动曲线如图5～图8。

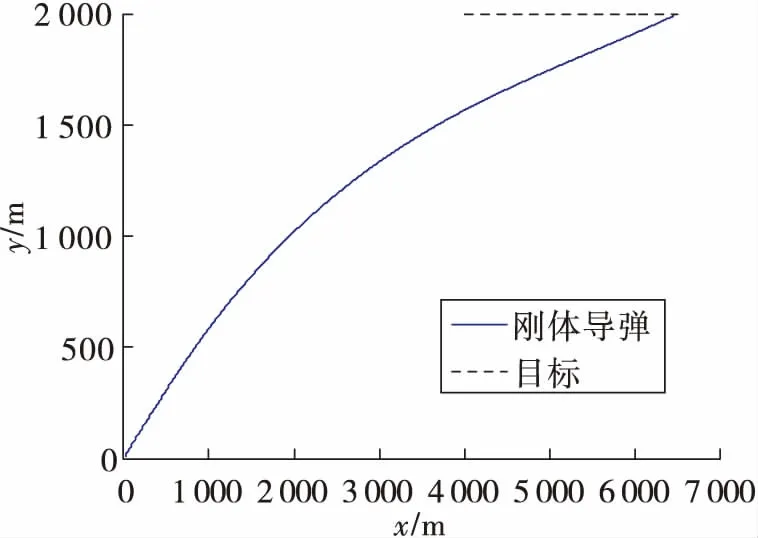
图5 刚体导弹的弹道曲线

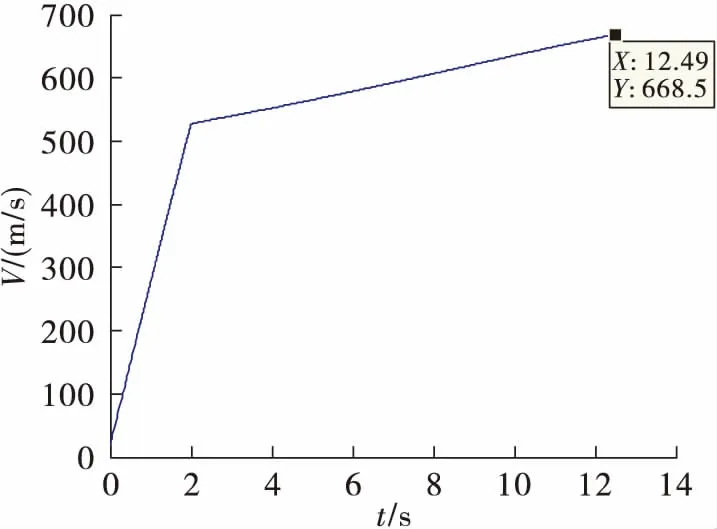
图6 刚体导弹的速度变化曲线

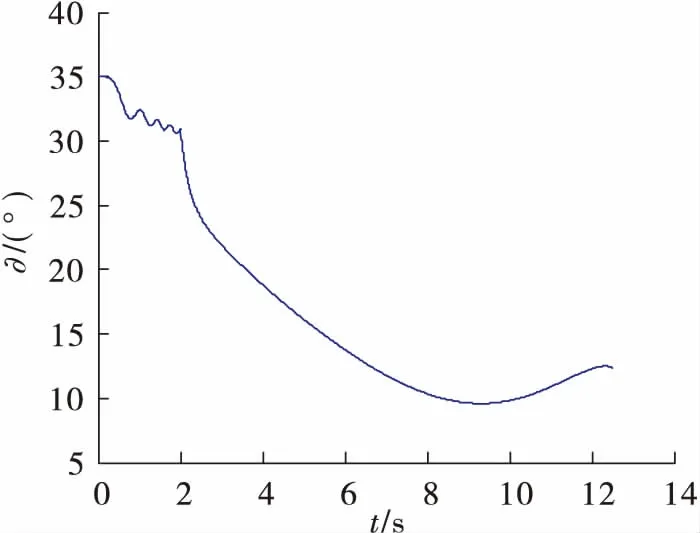
图7 刚体导弹的俯仰角变化曲线

图8 刚体导弹的俯仰角速度曲线

从上述曲线可以看出，当把导弹作为刚体时，导弹在大约12.4 s击中目标，导弹末速度为668.5 m/s，击中目标时导弹的俯仰角在13°左右，满足击中条件。

当考虑气动弹性时，在程序中切换程序模式，选择模型为考虑气动弹性的模型。对考虑气动弹性的弹性体导弹进行仿真，将得到的仿真结果与只考虑刚体模型情况下作直观的对比，得到仿真曲线如图9～图15。

4 仿真结果分析

根据上面的仿真结果，对比考虑气动弹性的弹性体导弹和刚体导弹的飞行参数可以看出，在图9的弹道对比曲线中，可以看出两组弹道在末时刻相差约25 m，相比于弹径来说，大致是弹径的100倍左右；在图10的速度曲线对比中，二者末时刻速度相差大约20 m/s，从图11和图12的变化曲线可以看到，当导弹末速度达到660 m/s时，导弹的俯仰角和俯仰角速度发生剧烈变化，说明此时在气动弹性的影响下，测量误差发生极大变化，导弹出现严重颤振，这对导弹的飞行是极为不利的，这是需要在后续控制系统设计时需加以改进来避免的问题。图13～图14也很好的验证了这一现象，对于考虑气动伺服弹性的导弹，导弹在末时刻发生了严重的变形，弹身振动十分剧烈，并且导弹头部和尾部的变形量是导弹中部变形量的10～20倍，这对以后的研究有一定的启发意义，即可以考虑将敏感装置安置在变形较小的位置，用来减弱弹性振动对导弹飞行状态的影响。

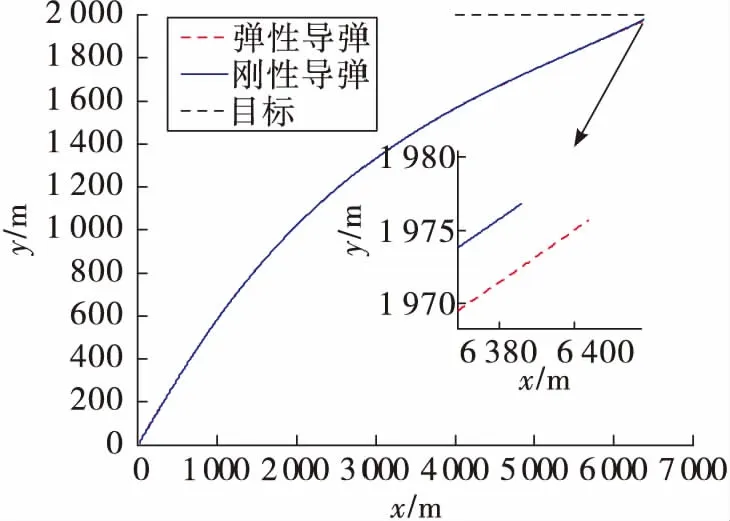
图9 弹道曲线对比

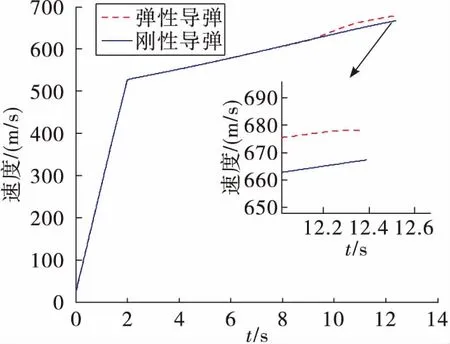
图10 速度曲线对比

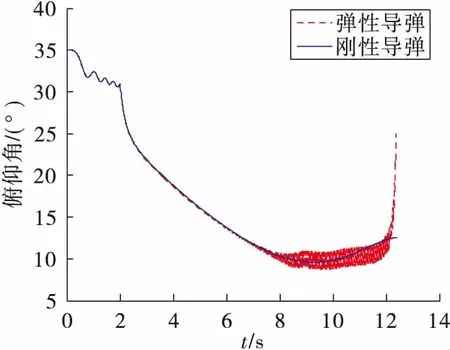
图11 俯仰角曲线对比

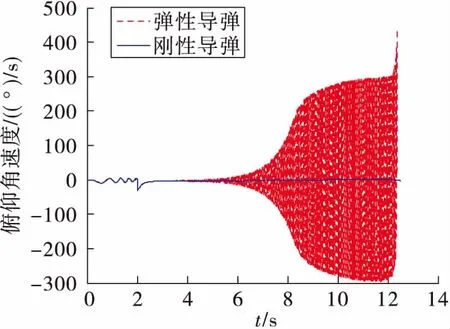
图12 俯仰角速度曲线对比

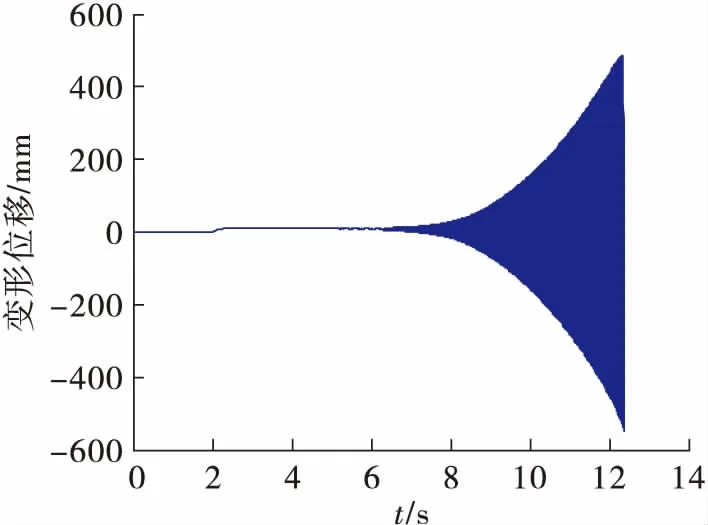
图13 弹体头部变形量曲线

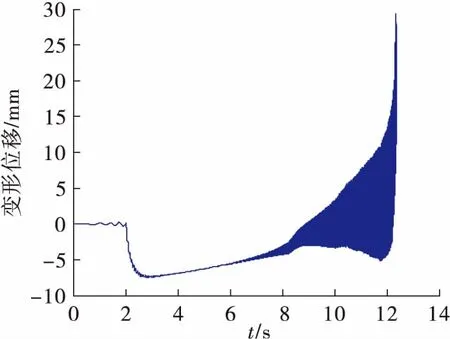
图14 弹体中部变形量曲线

图15 弹体尾部变形量曲线

5 结论

从仿真结果可知， 气动伺服弹性对导弹飞行状态有显著的影响，弹体发生变形后，推力偏心的作用对控制系统的影响较大，推力偏心项在纵向对称面内的分量会对导弹受力产生影响，这种现象在建模时不应该被忽视。考虑气动伺服弹性的影响时，仿真结果表明，弹性振动对导弹弹道与速度和俯仰角的影响相对较小，而对俯仰角速度影响较大。通过上述仿真结果可以得到如下结论：

1)弹性振动引起的推力偏心对导弹影响在动力学建模时需要考虑。

2)弹性振动引起的测量误差被弹上敏感元件测量并给回到控制系统中，控制系统给出“错误”的控制输出会激励这种误差越来越大，即气动伺服弹性的存在会对导弹飞行状态产生很大的影响，导弹飞行速度达到大约2Ma时，可以看到弹身发生了严重的变形量，如果这种影响长时间存在的话，严重时会导致弹身折断。

3)在之后的研究中，可以通过考虑对控制系统进行改进，运用现代控制理论避免发生严重的弹性振动。

4)当导弹命中精度要求很高时，弹性振动引起的非定常气动力不能被忽视，因为这会导致弹道产生误差，对导弹精度产生影响。