无滞后激光驾束制导系统研究*

李 召，徐文旭，黄 鹏

(1 中国人民解放军63961部队，北京 100000； 2 西安现代控制技术研究所，西安 710065)

0 引言

激光驾束导弹制导系统通过线偏差测量方式测量导弹相对于激光信息场中心的位置偏差，生成控制指令，控制导弹沿着信息场中心飞行。为了保证导弹的稳定性，传统的制导系统都包含相位超前校正网络，导致导弹在攻击运动目标时存在系统滞后。为了减小或消除这种系统滞后，可采用两种方法：一是在反馈校正网络中串联相位滞后环节；二是在瞄准装置安装角速率传感器，测量瞄准线的转动角速率，然后生成一个与瞄准线角速率成比例的跟踪指令。但是这两种方法均存在一定的缺陷，前者会导致系统响应时间延长；后者不仅需要安装相应的角速率传感器，而且还必须通过无线电波传输到弹上计算机，额外增加了系统成本。

为了避免这些缺点，文中提出了一种新方案，不增加系统附加成本，且能够减小导弹在攻击运动目标时的滞后。具体实现途径为：采用卡尔曼滤波技术估计瞄准线的转动角速度，然后生成一个与转动角速度有关的跟踪指令，与导弹的控制指令合成，控制导弹运动，解决导弹在跟踪运动目标时的滞后问题。

1 无滞后驾束制导系统

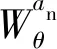
文献[1]给出了附加补偿角偏差θ′(t)的计算过程。附加补偿加速度aN(t)的计算公式见式(1)。二者原理相同，只是附加补偿的加入点不同。

(1)

式中：右端第一项为瞄准线转动产生的切向加速度，第二项为瞄准线转动和导弹线运动相互影响产生的哥氏加速度。

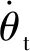
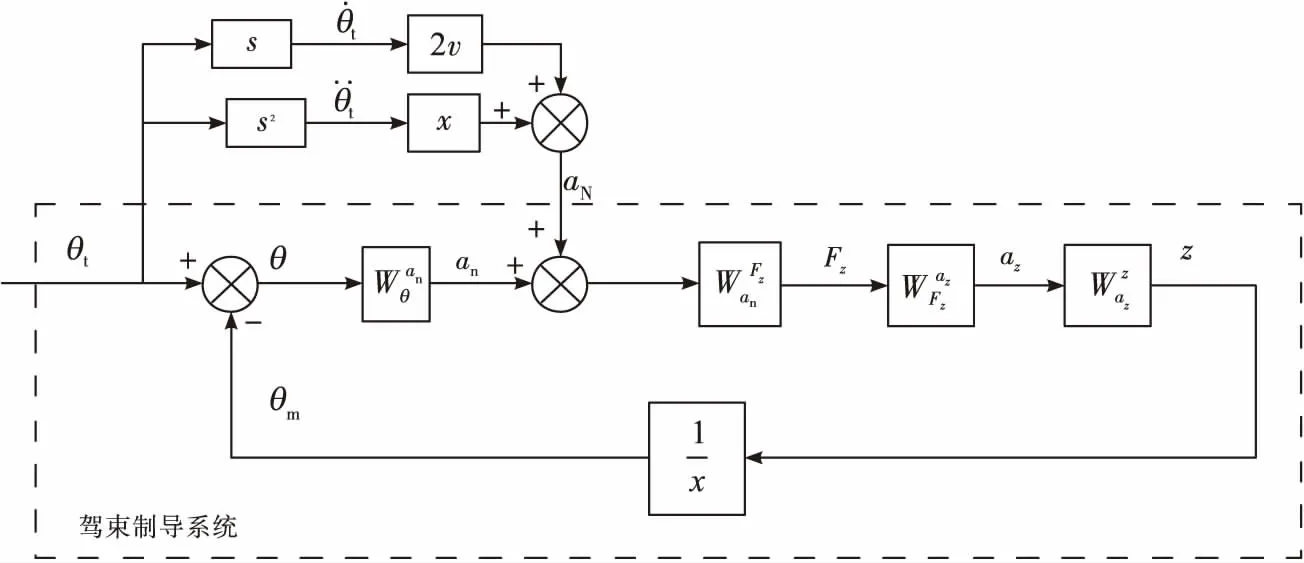
图1 无滞后驾束制导系统原理框图

2 瞄准线转动规律的卡尔曼滤波估计

2.1 具有控制作用时的连续卡尔曼滤波方程

设连续系统的状态方程和量测方程[2]为

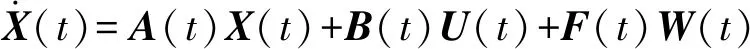
(2)

Z(t)=H(t)X(t)+V(t)

(3)

式中：X(t)为n维状态向量；A(t)为(n×n)阶状态转移矩阵；B(t)为(n×p)阶控制驱动阵；U(t)为已知的p维控制向量；F(t)为(n×r)阶系统噪声矩阵；W(t)为r维随机干扰向量；Z(t)为m维量测向量；H(t)为(m×n)阶量测矩阵；V(t)为m维量测噪声。

该连续模型对应的等效离散状态方程和量测方程为：

(4)

Z(ti+Δt)=H(ti)X(ti)+V(ti)

(5)

式中:

(6)

记X(ti+Δt)为Xi+1，Φ(ti+Δt,ti)为Φ(i+1)/i，其它符号采用相似记法。记qi=Qi/Δt，ri=Ri/Δt，Qi为等效离散系统噪声方差阵，Ri为等效离散系统量测噪声方差阵。则等效离散系统的卡尔曼滤波基本方程为:

(7)

(8)

(9)

(10)

Pi+1=(I-Ki+1Hi+1)Pi+1,i

(11)

初始条件为:

(12)

2.2 瞄准线转动规律的卡尔曼滤波模型

以某激光驾束制导反坦克导弹偏航通道为例，根据导弹动力学模型和目标运动学模型，推导瞄准线运动规律的卡尔曼滤波模型。俯仰通道的结构和原理与偏航通道相同。

导弹与目标之间的二维运动关系如图2所示。图中，Axz表示地面坐标系；Axczc表示瞄准线坐标系；Oxbzb表示弹体坐标系；Ox3z3表示速度坐标系；Ox2z2表示弹道坐标系。

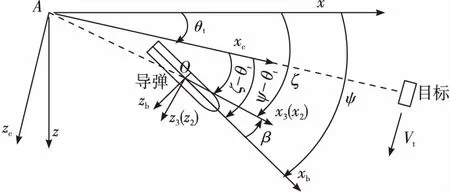
图2 导弹与目标运动关系示意图

1)侧滑角状态方程

根据牛顿第二定律，导弹在弹道坐标系Oz2方向上的加速度可表示为:

(13)

等式右边分别为控制力、发动机推力和空气动力在Oy2方向上的投影，表达式分别为[3]:

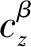
ψ、ζ和β之间的关系为:

ζ=ψ-β

(14)

将式(14)代入式(13)得：

(15)

即

(16)

由于β为小角度，对式(16)进行线性化得到侧滑角的状态方程:

(17)

2)偏航角角速度状态方程

根据动力矩定理，可知

(18)

式中:Jy为导弹赤道转动惯量；My为导弹在偏航方向上受到的总力矩，My的表达式为:

My=M1+M2+M3

(19)

式(19)右边第一项为偏航静稳定力矩，第二项为偏航阻尼力矩，第三项为偏航控制力矩，表达式分别为[3]:

(20)

式(18)、式(19)和式(20)联立得到导弹偏航角角速度状态方程：

(21)

3)导弹位置状态方程

根据牛顿第二定律，导弹在瞄准线坐标系zc方向的运动学方程可表示为：

(22)

式(22)右边分别为控制力、发动机推力和侧向力在Ozc方向上的投影，表达式分别为[3]：

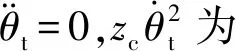
(23)

(24)

这样就得到了导弹位置状态方程。

联立式(17)、式(21)和式(24)，并加入瞄准线转动角速度状态量，卡尔曼滤波器的状态方程见式(25)，状态向量中能够被观测量为zc，见式(26)。

(25)

zc=x·(ψ-β-θt)

(26)

激光驾束制导反坦克导弹为了实现姿态调整与稳定，弹上装有角位置陀螺仪，可以实时测得导弹的3个姿态角。因此，导弹偏航角ψ也是一个可观测的量。不考虑观测噪声的观测方程为:

(27)

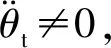
3 仿真研究

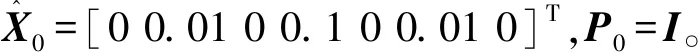
仿真采用Matlab软件的定步长计算，弹道方程的求解步长为0.1 ms，弹道方程和卡尔曼滤波器的更新步长为10 ms。仿真得到导弹的瞄准线转动角速度θt估计结果如图3所示，附加补偿加速度指令aN(t)如图4所示。由于在初始飞行段，弹体姿态散布较大，控制系统主要对导弹的姿态进行调整，而且瞄准线转动角速度的估计值在初始段也没有收敛到理想值附近。因此，附加补偿加速度在导弹飞行2 s后加入。无附加补偿和有附加补偿的zc曲线如图5所示。

从仿真结果可以看出，对瞄准线转动角速度的估计结果较为准确，附加加速度补偿指令有效的消除了驾束制导系统的滞后。

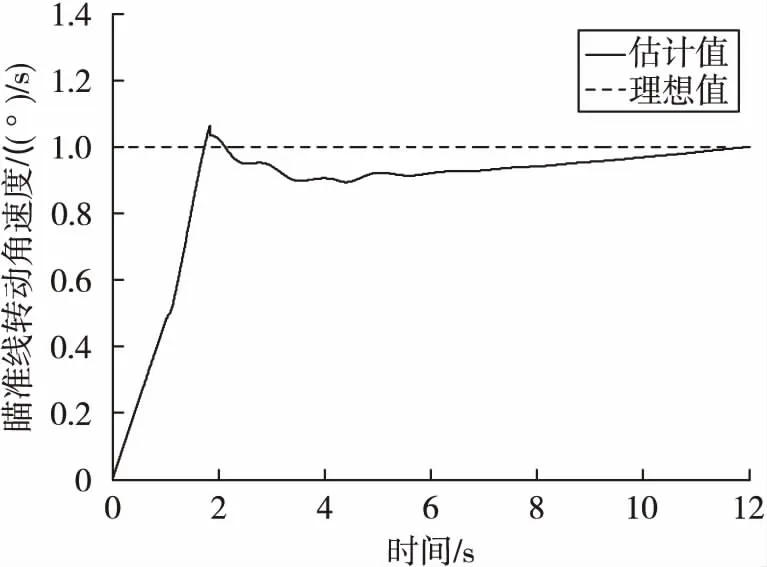
图3 瞄准线转动角速度的估计值

4 结论

文中提出了一种无滞后驾束制导系统方案，该方案利用卡尔曼滤波算法估计激光束的转动角速度，生成前馈附加控制指令；推导了附加加速度指令的计算公式，建立了卡尔曼滤波器的模型，以某型反坦克导弹参数进行了数字仿真研究。仿真结果表明，无滞后驾束制导系统方案可行，设计方法可为采用卡尔曼滤波技术实现驾束制导导弹无滞后飞行提供理论支持，也可用于类似产品设计中。

图4 附加补偿加速度指令

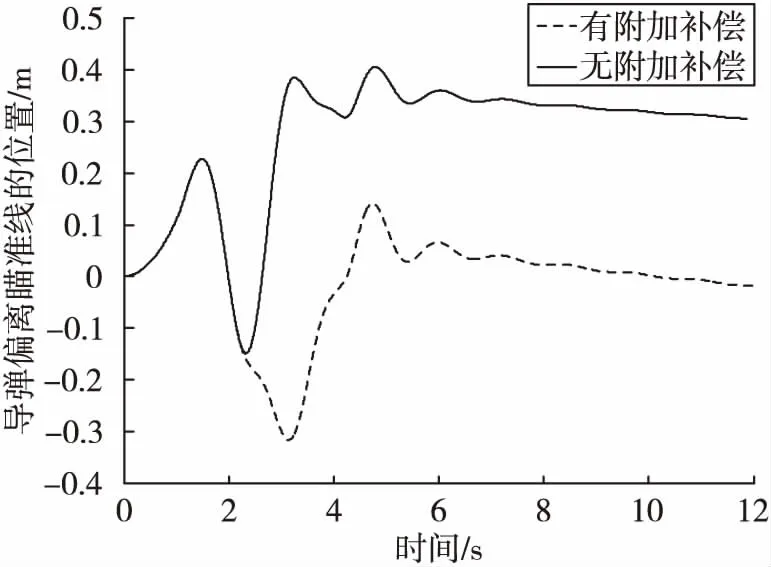
图5 导弹的位置偏差