一体化飞行器面向控制的建模与弹道规划*

2020-07-09刘知贵刘志勤王庆凤

弹箭与制导学报 2020年1期

黄俊，刘知贵,3，刘志勤，王庆凤，张勇

(1 中国工程物理研究院电子工程研究所，四川绵阳 621900； 2 西南科技大学计算机科学与技术学院，四川绵阳 621010；3 西南科技大学信息工程学院，四川绵阳 621010； 4 中国空气动力研究与发展中心高超中心，四川绵阳 621000)

0 引言

乘波构形、气动推进一体化设计[1]在升阻特性和进气道流量捕获特性上的优势，是吸气式高超声速飞行器气动布局的重要选形，该选形飞行器简称一体化飞行器。美国的X-51A[2]的一项重要技术验证即是乘波构型一体化设计且被命名为乘波者。美澳联合的HIFiRE[3]、法德联合的JAPHAR[4]等项目开展一体化飞行器的基础技术研究。我国贺旭照[5]、卫峰[6]等对乘波进气道的设计方法开展深入研究并取得较好成果。一体化飞行器在设计方法不断发展的现状下，对其气动与控制特性的研究需求日益显著。文献[7]对采用少量CFD数据结构工程计算方法对HIFiRE6的飞行动力学进行分析。文献[8]给出了X-51A的特定状态的静稳定性分析。文献[9]在参数化方法生成一体化飞行器基础上采用工程计算和多项式拟合方法面向控制建立气动力模型。相关研究在逐步拓展到控制领域，因此适时开展一体化飞行器的可控制性、可飞性、飞行可达性的度量是必要的。文中建立一体化飞行器的“计算、建模、分析”全程快速方法，作为一体化飞行器设计初期的快速性能评估工具。

近年X-51A相似飞行器是一体化飞行器气动特性的计算主要研究对象。周正[10]借助X-51A飞行器影像资料构建了相似飞行器并对巡航条件下的气动特性分析；文献[11-12]对X-51A相似飞行器的巡航气动特性进行分析。这些研究结果给出飞行器在巡航条件下的升阻特性，但单一条件的气动数据，无法支撑控制相关研究工作开展。气动推进一体化高超声速飞行器的气动、推进、控制相互耦合，气动数据的获取是一个巨大的难题。例如，美国X-51A[8]项目，在NAART、PSWT等风洞中试验，风洞时间超1 720 h，运行达3 200次。采用CART3D-Euler等解算器进行数值模拟，总共使用78套网格，运行1 982次。飞行器轨迹、制导和控制等问题研究人员难以独立完成。因此，面向控制相关问题，有必要开展快速计算型号数据集与建模的方法研究。

意大利航空航天中心(CIRA)[13]利用增量法(build-up approach)对PRPRA-USV1高超声速飞行器实现风洞试验与数值计算数据的融合建模，并阐述了方法的有效性。增量法是控制建模经典方法，如美国X34[14]航天飞机中应用增量法建立数据集。文中借鉴上述具体型号研制过程的数据建模思路，通过数值方法模拟X-51A相似外形飞行器的数据集构建并建模，为控制方法研究提供数据基础。在X-51A研制单位美国空军研究实验室(AFRL)的公开报告[8]中对X-51A进行了静稳定性分析，文中在气动力模型输出数据基础上分析静稳定性数据，并与之对比，获得相同结论，表明文中气动力模型具备该类飞行器气动特性。

弹道规划是总体设计中对飞行器可控性、可飞性、可达性分析的重要途径。文中提出基于伪谱法计算X-51A相似飞行器的最大航程滑翔弹道，同时验证建立模型的完备性，仿真结果表明建模方法与弹道求解的可行性与有效性。

1 计算模型与方法

以一种与X-51A气动外形相似的气动推进一体化飞行器模型为研究对象，如图1所示。模型参数见文献[10]。根据后文气动模型建立的最小数据集需求，参考文献[8]中弹道特性分析飞行走廊，按飞行走廊设置计算条件，计算条件设置如表1所示。

图1 一体化飞行器数模

表1 计算条件表

Ma∞H/kmα/(°)δp/(°)3.054.5185.0215.5246.028-10～10间隔20(通气)-15～15(不通气)

为了获得不同高度的气动数据，对每一个马赫数补充计算两组不同高度数据，如表2所示。

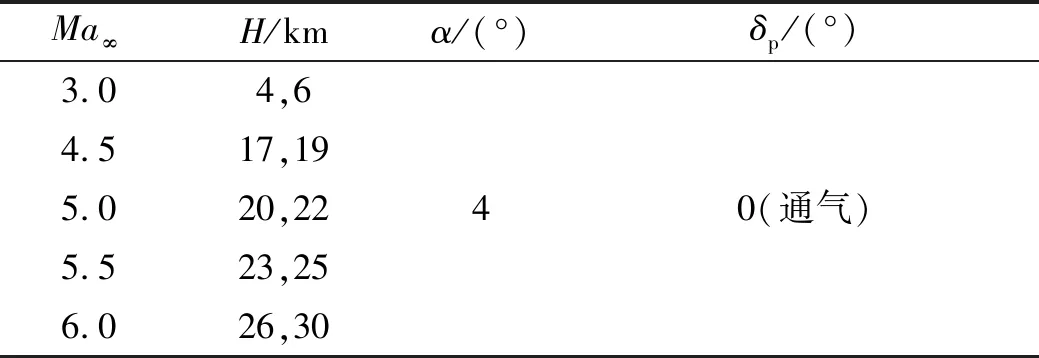
表2 计算条件表

文中以Fluent软件作为计算工具，采用SST方程k-ω模型进行数值求解N-S方程。

舵是最重要的气动控制机构，为了获得不同舵偏角下的气动特性，制作了不同舵偏角模型网格。为了提高计算速度，采用三维半模网格，如图2所示；同时在计算舵偏数据时采用不通气半模网格；舵偏角每5°生成一套网格，其中零舵偏有通气与不通气半模网格，因此共8套网格，如图3所示。

图2 δp=0° 局部体网格

图3 总共生成8套数模(网格)

2 增量建模方法

首先，定义气动模型无量纲输出分别为升力系数、阻力系数、俯仰力矩系数，如式(1)。其中Sref=1 m2,bref=1 m，力矩参考点取(0.55L,0,0)。

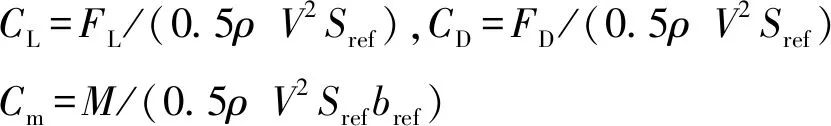
(1)

式中：FL为升力，FD为阻力，M为俯仰力矩。

按照前一章节计算，则可获得数据集：

{Ma，Re,α,δp,CL,CD,Cm}

(2)

式中：Ma表示马赫数；Re表示雷诺数；α表示攻角；δp表示俯仰通道数值舵偏角。文中模型如图1所示，采用了全动平尾和双立尾，物理舵面的控制方式为：

(3)

按照增量法思想，纵向全局气动力系数可表示为：

(4)

式中：考虑一体化飞行器的耦合特性，右端各项分别代表了基准、俯仰通道的贡献，两者的表达式为：

(5)

借鉴X-51A地面试验经验，攻角和舵偏角作为基本组合，具有较多的维度值，因此将各个贡献表示为以下回归形式：

(6)

针对气动布局的特点，舵偏角的贡献进一步简化，文中忽略雷诺数的影响，忽略侧滑角对偏航通道控制的影响，忽略升降舵位置对差动效率的影响，由此得到：

(7)

在基准贡献中，雷诺数外推是非常关键的环节。基本的雷诺数修正数据可通过数值模拟方法得到，那么，变雷诺数气动力数据表示为以下回归形式：

Ci(Ma,Re,

(8)

于是，通过平移变换，基准贡献可以表示为：

Ci(Ma,

(9)

对于不同高度的气动数据，采用雷诺数修正获得。飞行高度、大气参数、雷诺数建立关联关系：

(10)

式中:ρ、v、L、μ、T、c分别表示密度、速度、飞行器长度、粘性系数、大气温度、当地声速；atmos为参照1976版美国标准大气表编写的插值函数。

可见，增量法分别得到各个贡献的气动力“数据立方体”。同时，增量法提出了气动力建模的最小数据集需求，这就为地面试验、数值模拟的试验设计提供了依据。

3 计算结果与模型建立

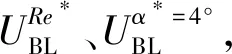
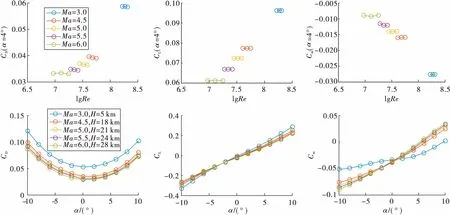
图4 基准数据集和

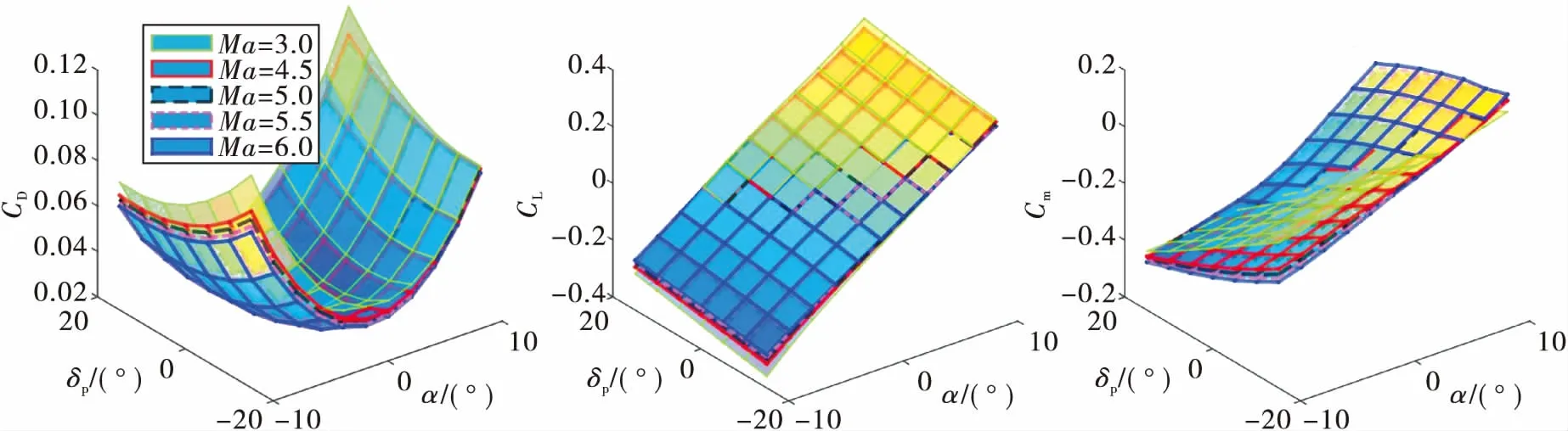
图5 舵效数据集

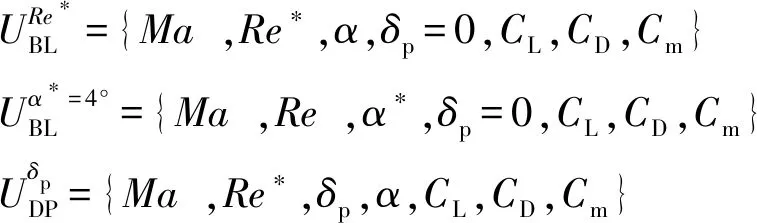
(11)

按照前述增量建模理论，设计如图6所示流程构建增量模型。由于气动数据集变量较多、样本少，且变量间存在相互耦合的相关关系，建模过程中的拟合采用一种基于偏最小二乘法的多维拟合法来实现。

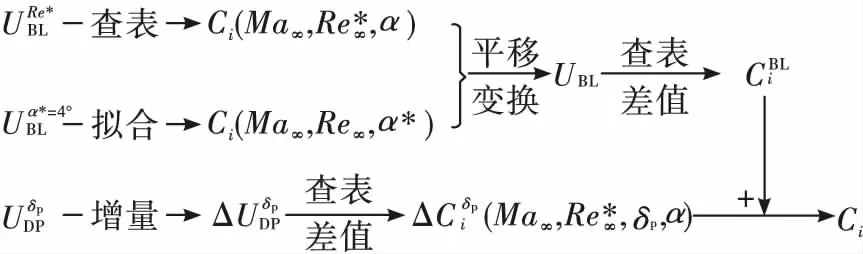
图6 增量模型构建流程图

对于基准数据，考虑雷诺数外推，不可避免带来误差。如图7，在马赫数为4.5时，源数据是18 km，通过雷诺数外推获得17 km和19 km的气动阻力系数，其误差在10-4级别，符合控制问题研究需求。对于舵效数据已计算全维度的笛卡尔积数据集，直接查表内插值即可获得任意维度的舵效增益数据，图8给出模型在马赫数为4.5时舵效增益。

图7 基于基准数据模型误差

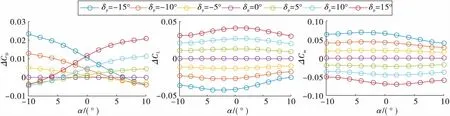
图8 舵效增益模型输出(Ma=4.5)

4 模型纵向静稳定度分析

文中采用“瞬时平衡”假定飞行轨迹是定态飞行的。为了使飞行器在某一飞行攻角下纵向平衡，俯仰舵必须偏转相应角度。如图9(a)中给出了各个速度和对应高度下的配平曲线δp=f(α)，曲线给出了攻角在-10°～10°范围的配平舵偏，表明了在此姿态角范围内，舵偏角能够使飞行器纵向平衡。

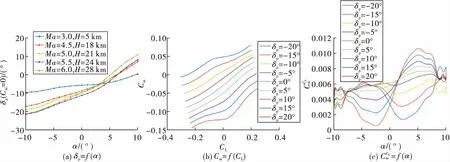
图9 稳定性分析

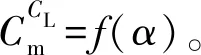
5 滑翔弹道规划

弹道规划为导弹性能指标和总体设计的可行性提供重要参考依据。前文建立的气动力模型为弹道计算的重要基础。下文以最大滑翔距离优化目标的弹道规划为建立模型的应用算例。滑翔初始高度为27 km、速度为6Ma；末端高度为1 km、速度为3Ma；根据稳态配平结果，全程攻角约束为-8°～8°。建立最优控制问题如下：

(12)

(13)

式中：[h,v,γ]为轨迹状态量的离散向量，离散点(节点)数为n；FD、FL为离散的阻力和升力向量，由前述增量模型查表插值获得；wi为积分算子，D为微分矩阵。设置节点数n=32。

Matlab仿真结果如图10所示，滑翔时间351.2 s，滑翔水平距离484.8 km；δp是对应飞行姿态下保持纵向平衡的俯仰舵偏；系统伪谱法离散正解与仿真反解的对比证明了获得解的可行性，同时也验证了文中所建立的气动力模型足够支撑该类飞行器的控制特性研究。

如图11所示，文中的伪谱法改进了控制量插值，采用分段3次埃尔米特插值(PCHIP)，解决了控制量的Lagrange多项插值因Gipps现象使控制量超出控制约束边界的问题。

6 结论

面向飞行器控制特性研究需求，系统完成了对一种一体化飞行器的气动数据计算、建模与分析应用的集成研究，获得结论如下：1)文中的增量法能够指导算例设计以较小的代价获得足够构建面向控制建模的数据集，并建立面向控制的气动力模型；2)静稳定度分析结果表明，文中模型具有与X-51A相同的气动特性，是静不稳定的，为了维持飞行的姿态平衡，需要及时控制舵偏加以配平；3)提出改进伪谱法计算出可配平攻角约束下，以最大航程为目标优化的可行弹道，估计出文中模型的滑翔部分弹道滑翔水平距离可达484.8 km，验证了建模方法与弹道求解的可行性与有效性。