五棱镜角度制造误差对转向角的影响

温中凯 张庆君 李爽 雷文平 黄颖

（1 南京航空航天大学航天学院，南京 210016）（2 北京空间飞行器总体设计部，北京 100094）（3 北京空间机电研究所，北京 100094）

0 引言

五棱镜具有使主截面内光路垂直折转且不产生镜像的光学特性[1]，在工程中应用十分广泛，如采用五棱镜扫描法进行波前检测[2-4]、利用五棱镜的折转特性进行平行光管的焦面监测[5-6]、利用五棱镜检测光学元件面形[7-10]等。在空间光电跟瞄系统中，常利用大口径平行光管与五棱镜的组合来进行各光电子系统的光轴平行性标校，五棱镜的制造误差将直接影响多光轴平行性的标校精度，因此，需要对五棱镜进行误差分析以修正测试结果。

目前，普遍认为五棱镜对光线折转影响最大的误差源是五棱镜的角度制造误差，该误差会影响五棱镜的一维不变性，造成转角误差，进而影响测试结果的精度。针对当前计算五棱镜角度制造误差影响的方法混乱，各方法计算精度不高的情况，本文从各方法的理论基础入手，结合工程中实际应用的五棱镜，给出了相应的计算公式、计算范围以及计算误差，并推导了一种在所有情况下计算结果均与真值相等的新方法，对实际工程应用具有较强的现实意义。

1 光线转角误差的几种常规算法

五棱镜是常见的光束定角度转向器之一，有两个折射面和两个反射面，光线经理想五棱镜的两次折射与两次反射后可折转90°，其主截面示意如图1 所示。

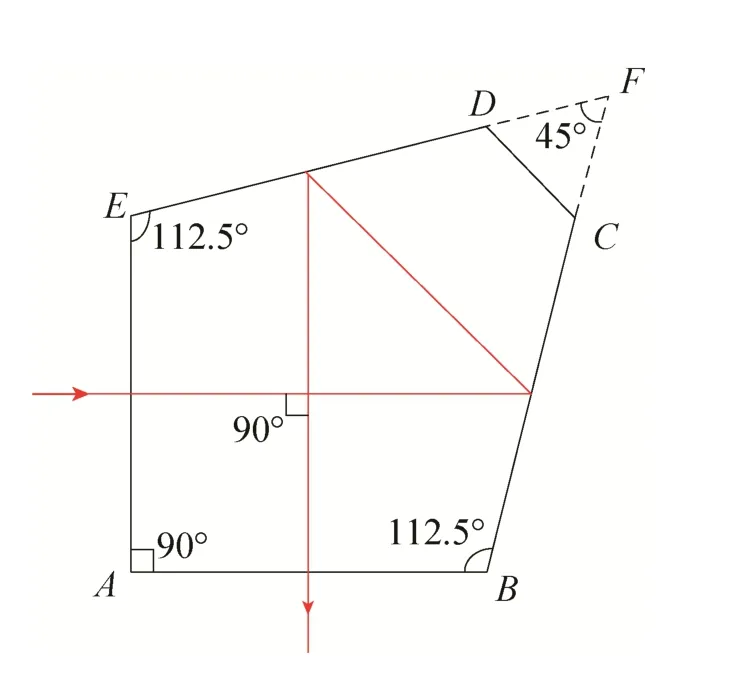
图1 理想五棱镜主截面示意Fig.1 Sketch of principal section for ideal pentaprism

工程应用中的五棱镜不可能绝对理想，制造误差主要体现为主截面内的∠A、∠B、∠E和∠F与理想值不同。角度制造误差的存在，将改变五棱镜的光线恒转特性，直接影响五棱镜的工程应用结果，故有必要对其影响进行计算以修正测试数据。

1.1 理论求解方法[11-12]

五棱镜光线追迹法是一种以矢量折反射定律作为理论基础来求解光线转角误差的方法，也是公认的理论求解方法，其结果可作为真值用于评价其他方法的计算精度。

设存在角度制造误差的五棱镜为ABCDE—A′B′C′D′E′，其共有4个工作面，按照与光线接触的先后顺序分别设为P1～P4，各工作面的法向量分别设为N1～N4。以点A为坐标原点，P1为YOZ面，ABCDE面为XOY面建立如图2 所示的空间直角坐标系。

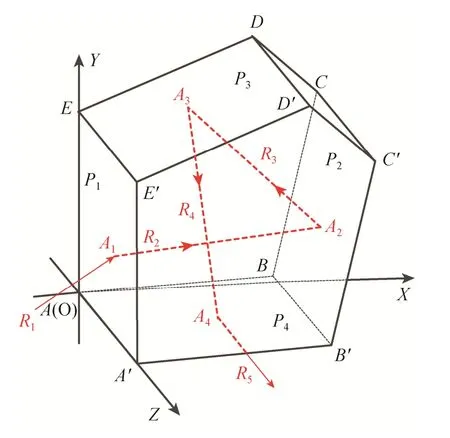
图2 五棱镜作用光路Fig.2 Light path map of pentaprism

由图2可知，光线被4个工作面分成了5部分，按照先后顺序分别设各光线的单位方向向量为Ri(mi,ni,pi)，其中i=(1,2,3,4,5)，mi,ni,pi分别为Ri正向与X、Y、Z坐标轴正向夹角的余弦，由空间解析几何可得各工作面的法向量分别为

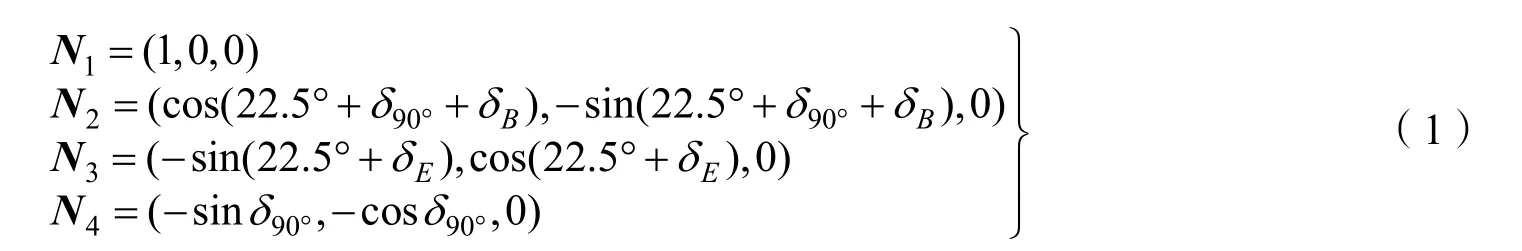
式中δ90°、δB、δE和δ45°分别为图1 所示的五棱镜主截面内∠A、∠B、∠E和∠F这4个角的制造误差。

对各个工作面依次应用矢量折反射定律，可得存在角度制造误差五棱镜的出射光线向量求解公式为

则五棱镜角度制造误差所产生的真实光线转角误差θ为

1.2 工程中常用的几种方法

虽然理论求解方法的计算结果为真值，但却占用了较大的计算资源，故实际应用中常采用其他方法来分析五棱镜角度制造误差所产生的光线转角误差。目前常用的方法有二倍反射角法、第一光学平行差法、综合开方法、展开平板光楔法、展开平板光线追迹法、几何关系分析法、泰勒展开近似法等。

（1）二倍反射角法[13-14]

二倍反射角法认为，五棱镜属于二次反射棱镜，作用相当于一个双面镜，其出射光线与入射光线的夹角取决于两个反射面的夹角，即光线的转角误差由δ45°决定，计算公式为

此法仅需对δ45°进行单独测量便可估计光线的转角误差，节省了工程量，但精度不高。

（2）第一光学平行差法[15-16]

第一光学平行差法认为主截面内的光线转角误差的大小与δ90°和δ45°有关，同时也受五棱镜折射率n的影响，具体计算公式为

该方法综合考虑了折射率和角度制造精度的影响，精度较高，但没有考虑光线入射角的影响。

综合开方法认为五棱镜的光线转角误差主要由δ45°与δ90°所决定，两者各自产生的误差分别为2δ45°和所产生的综合误差为

该法与二倍反射角法类似，虽计算方便，但计算精度不高。

（4）展开平板光楔法[19-21]

展开平板光楔法认为存在角度制造误差的五棱镜可展开成一个光楔（见图3），光线转角误差由五棱镜展开平行平板楔角和五棱镜折射率n决定，计算公式为

该方法便于进行五棱镜和其他光学组件的综合光路分析，但没有考虑光线入射角的影响。

（5）展开平板光线追迹法[22]

展开平板光线追迹法认为光线转角误差不仅与平板楔角α和五棱镜折射率n有关，还与入射角I的取值有关。光线的作用过程如图4 所示，图中I′为出射角。由图4 所示几何关系可得光线转角误差为

图3 五棱镜展开示意Fig.3 Expanded schematic of pentaprism

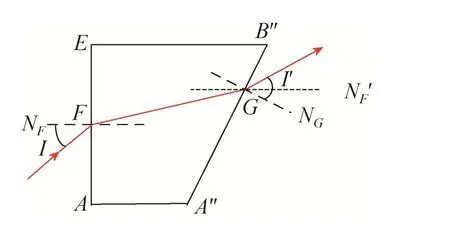
图4 展开平板光线追迹示意Fig.4 Ray tracing diagram of unrolled plate

该方法易于进行五棱镜和其他光学组件的综合光路分析，但不适合δ45°值较大的五棱镜使用。

行方式由传统模式向“四化”模式转变，功图计量系统应用代替了传统人工计量、计量站计量。远程采集控制终端（RTU）应用实现了数据自动传输和远程控制，提升了智能化管理；视频监视系统应用实现了现场监控及可视化管理。

（6）几何关系分析法[23-24]

该方法通过分析五棱镜主截面光线的折转情况，根据图 5 所示的几何关系推导出光线转角误差为

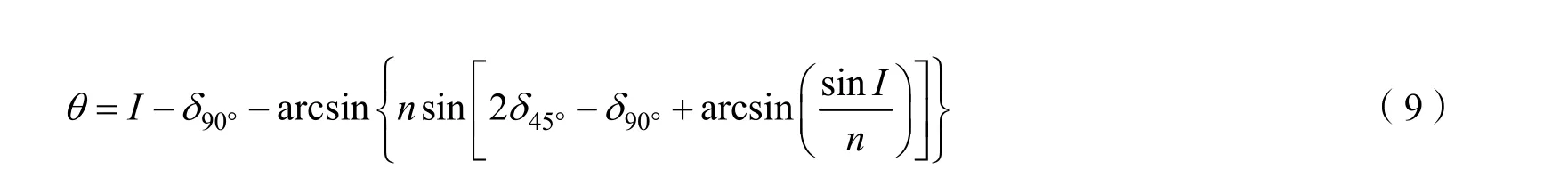
几何关系分析法的精度较高，但其计算公式只通过一种形式的光路推导得出，说服力不足。

（7）泰勒展开近似法[25]

根据几何知识，并结合多项式泰勒展开，光线转角误差θ可近似表示为

式中n1，n2分别为五棱镜外部环境的折射率和五棱镜折射率。该方法精度较高，且主要应用于外部环境非真空或非空气的场景下。

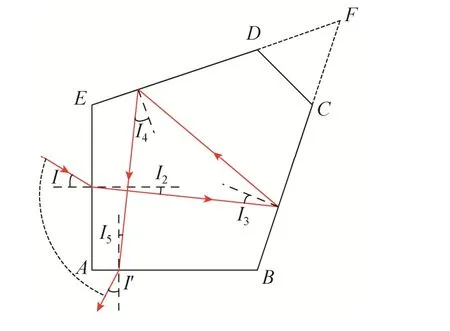
图5 五棱镜光路几何关系Fig.5 Geometric relation of pentaprism optical path

2 几何符值法

本文以空间解析几何为基础，代入符号规则推导了一种既可描述所有可能情况，计算结果又与真值相吻合的计算角度制造误差影响的方法。推导过程中所有角度的符号均采用国家标准（GB/T·1224-1999）的规则，并按标准对光线与法线夹角的符号正负做出了如下规定：由光线以锐角方向转向法线，顺时针为正，逆时针为负。故可根据五棱镜入射角I1和出射角I4′的符号正负进行组合分类，有4 种可能的情况：该4 种情况的光线示意如图6所示。

对于组合①，即I1＞0 、I4′ ＞0时，在P1面上应用折射定律有为光线在P1面上的折射角），过点F、G分别作P1面、P2面的法线NF、NG交于点H，将符号规则代入几何关系进行分析计算可得光线在P2面上的反射角I2′为

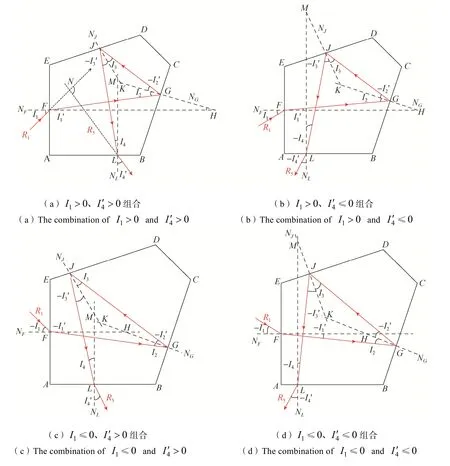
图6 五棱镜几何光路示意Fig.6 The diagram of pentaprism geometric light path

过点J作P3面的法线NJ交NG于点K，同理分析得光线在该面上的反射角I3′为

过点L作P4面的法线NL交NJ于点M，同理分析得光线在该面上的入射角I4为

对P4面应用折射定律有nsinI4=sinI4′，延长R1与R5交于点N，则R1顺时针转到R5即为光线的折转角β，且有

又知δ90°+δ45°+δE+δB=0，则光线转角误差为θ=β- 90°，即

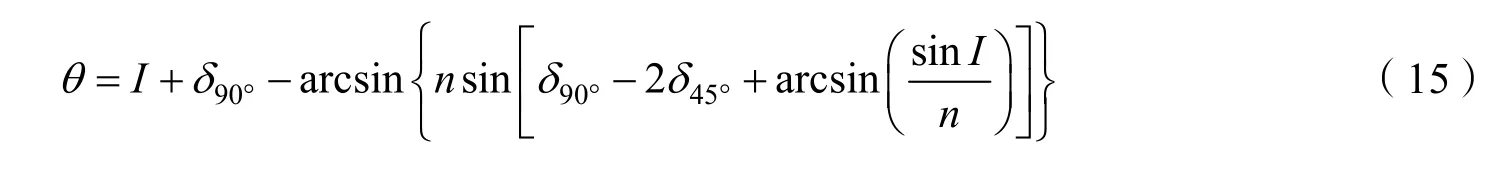
同理，对组合②、③、④依次分析，所得光线转角误差计算公式形式完全相同。

3 各求解方法对比分析

工程中五棱镜的使用往往需要计算光线通过不同位置或者持续变化状态下五棱镜出射光线的变化，所以有必要研究不同入射角条件下转角误差的变化情况。本文分析所使用的五棱镜材料为K9，角度制造精度为20″，光波波长为632.8nm，K9 玻璃在该波长下的介质折射率为1.515088。根据符号规则，分别设定入射角I的取值范围为±5°、±0.5°和0°，并把这三种情况下各方法的计算误差（各方法所得结果与真值的差值范围）进行整理，结果如表1 所示。

表1 各方法在不同入射角条件下的计算误差Tab.1 The calculation errors of each method under different incident angles单位：（″）

根据计算结果可得几点认识：

1）五棱镜的光线转角误差仅由δ90°、δ45°以及光线入射角决定，而与Eδ和Bδ无关。

2）二倍反射角法、综合开方法、展开平板光楔法、展开平板光线追迹法的计算结果存在极大的超差，不建议进行使用。

3）第一光学平行差法、几何关系分析法、泰勒展开近似法以及本文所推导的几何符值法均有较高的计算精度。

为了进一步分析各方法的优劣，将I的范围定为±5°，分析上述这4 种精度较高的方法在五棱镜角度制造精度为100″、300″、500″时的计算误差（结果见表2）。

表2 不同制造精度条件下4 种方法的计算误差Tab.2 The calculation errors of the four methods under different manufacturing precision conditions单位：（″）

由表2 可知，随着五棱镜角度制造精度的降低，第一光学平行差法、几何关系分析法、泰勒展开近似法的计算误差均随之增大，其中第一光学平行差法的超差最为严重，另外两种方法的超差幅度大致相同。而本文所推导的几何符值法无论光线入射角亦或是角度制造误差如何变化，计算误差始终保持在（10−10）″的量级，且该误差可认为是程序算法的舍入误差，故可认为该方法所计算的结果恒为真值，在现有众多方法中属最优。

运用本文所给的几何符值法对角度制造精度为20″、100″、300″、500″的五棱镜分别进行分析，可得0°、±0.5°、±5°入射角范围下所产生的转角误差计算范围（如表3 所示）。

表3 不同入射角与制造精度对应的转角误差计算范围Tab.3 The calculation ranges of steering angle error corresponding to different incident angle and manufacturing accuracy单位：（″）

将±0.5°、±5°入射角范围下的计算结果与0°入射角的计算结果进行比较，可得入射角所产生的附加误差，如表4 所示。

表4 附加误差统计表Tab.4 Statistical table of additional error单位：（″）

通过比较表3～4 中不同制造精度的五棱镜在入射角为0°、±0.5°、±5°条件下的转角误差与附加误差计算结果，可以看出：光线转角误差主要由五棱镜制造精度决定，而与光线入射角的关系不大；当五棱镜的角度制造精度为20″时，±5°的入射角变化仅产生0.1971″的附加误差，相对误差仅为0.28%；当五棱镜的制造精度较低，比如当五棱镜的角度制造精度为500″时，±5°的入射角变化会产生5.5272″的附加误差，相对误差仅为0.31%，均远远小于角度制造误差所带来的影响。

4 结束语

本文对当前工程中常用的分析五棱镜角度制造误差影响的方法进行了介绍，给出了各方法计算光线转角误差的理论基础以及计算误差，并结合符号规则推导了一种任意光线入射角、任意角度制造误差下计算结果均为真值的新方法，对比分析结果显示该方法在当前所有计算五棱镜角度制造误差影响的方法中属最优。此外，通过对计算结果进行分析发现：五棱镜的光线转角误差仅由δ90°、δ45°以及光线入射角决定，而与Eδ和Bδ无关；光线转角误差的大小主要取决于五棱镜角度制造精度，而与光线入射角的关系不大。