大口径空间反射镜支撑变形误差分析方法研究

杨秋实 张继友 于建海 陈建丞 于秋跃

（1 北京空间机电研究所，北京 100094）（2 国防科技工业光学超精密加工技术创新中心（先进制造类），北京 100094）

0 引言

近年来，空间遥感技术的发展对大型光机系统中的大口径空间反射镜要求逐步提高，主要表现在反射镜口径由几百毫米增大到4m 量级；轻量化率从60%提高至85%；面形高度起伏均方根值（RMS）要求由0.020λ 提高至0.013λ（λ 为氦氖激光器波长，λ=632.8nm），这些都对现有的光学检测技术提出了更高的要求[1-2]。在实际的光学检测过程中，为了保证反射镜性能的天地一致性，通常需要设计专用的重力卸载装置来补偿大口径空间反射镜的重力变形[3-5]。由于重力卸载装置中促动器自身的灵敏度、气路控制精度及支撑工装的偏心等误差均会对输出的支撑力产生影响，使得实际输出的支撑力与计算所得理论支撑力产生偏差，该偏差支撑力会使由支撑引起的镜面变形与理论仿真计算所得重力卸载面形产生差异，造成支撑变形误差。大口径空间反射镜检测到的面形误差主要包含该支撑变形误差与面形加工残差两部分[6-8]。支撑变形不仅受支撑点接触方式和支撑点布局等因素的影响，还与反射镜材料力学性能以及自身结构相关。反射镜的结构刚度会随着反射镜口径的增大、轻量化率的提高而降低，从而导致其面形就越易受支撑变形的影响[9-12]。如果能从反射镜检测结果中分离出支撑变形误差，分析得到造成相应面形变化的偏差支撑力大小，对反射镜的高精度检测及重力卸载装置的设计与装调都具有重要意义。

对于具有回转对称结构的反射镜，旋转检测法是对支撑变形误差和镜面加工残差进行分离的有效方法，常用的旋转检测法包括单次旋转检测法、N次旋转检测法和N+1 次旋转检测法。单次旋转法的检测过程相对简单，通过一次旋转检测去除检测结果中的非对称面形误差，但由于拟合项数有限，只能得到被测镜面的低频信息，检测精度较低[13-15]；N次旋转法是在等角度间隔下进行N次面形检测，测量时间较长，检测精度较高[16-18]；N+1 次旋转法是在N次旋转法基础上，增加了一次任意角度的面形检测，可以得到更为丰富的面形误差信息，但由于受支撑工装等条件限制，难以在实际检测中实现任意角度的面形检测[19-21]。综上对比，N次旋转检测法可以兼顾检测精度和检测效率，更适用于对大口径反射镜进行检测数据处理，将支撑变形误差分离。

由支撑引起的镜面变形可分为两部分，一部分是镜面倾斜和平移等刚性位移，另一部分是由偏差支撑力造成的面形变化。在检测过程中，可以通过软件算法去除刚性位移部分的影响，因此，支撑对检测结果的影响主要为偏差支撑力的影响。大口径空间反射镜具有较为复杂的结构，设计优化时常采用有限元方法进行分析计算，若计算结果的准确度足够高，就可以通过仿真计算得到偏差支撑力与面形变化的关系。

本文提出了一种支撑变形误差的分析方法，首先应用旋转法将检测结果中的支撑变形误差分离，通过有限元仿真分析，建立偏差支撑力大小与面形变化量的关系曲线，并以反射镜实测面形变化规律作为衡量有限元仿真精度的依据，修正有限元模型，得到更为准确的关系曲线，从而确定产生支撑变形误差的偏差支撑力大小。结合某型号直径1300mm 非球面反射镜的检测实例，验证了该误差分析方法的可行性。该误差分析方法可用于提高空间反射镜的检测精度和重力卸载工装的设计与装调精度。

1 支撑变形误差分离原理

在地面检测条件下，大口径空间反射镜的检测结果包含了镜面加工残差和支撑变形误差

式中W表示在检测过程中由干涉仪直接获取的面形结果；S表示镜面加工残差；T表示支撑变形误差；x、y为镜面直角坐标系中的横向坐标与纵向坐标，坐标系的原点为反射镜参考表面的中心点，光轴方向为z轴。在数据处理过程中，为了进行泽尼克多项式拟合[22-23]，需要将检测时采取的直角坐标系转化为极坐标系，公式（1）变为

式中ρ、θ为极坐标系中的径向坐标和角度坐标。

N次旋转检测法是绕光轴进行N次等角度间隔的旋转检测，旋转角度α=2π/N。在旋转过程中，镜面加工残差随镜子旋转而旋转，而由于重力卸载装置不动，各支撑点支撑力不变，支撑变形误差不随镜子旋转而旋转，检测结果可以表示成：

N次旋转检测结果的平均值Wave为

式中m表示检测过程中的旋转次数为镜面加工残差的算术平均结果，为检测结果的中高频误差部分，反射镜的支撑变形误差T为检测结果的中低频误差部分。利用泽尼克多项式拟合，可以将检测结果平均值中的中低频误差提取出来，得到反射镜的支撑变形误差。

2 支撑变形的仿真分析原理

由支撑引起的反射镜微小变形属于弹性变形，计算求解时可使用弹性力学方法。弹性力学主要研究弹性物体在温度变化、边界约束和受外力作用时产生的应力、应变和位移。在计算反射镜支撑变形量时，认为材料满足完全弹性、均匀性、连续性等条件，且支撑变形大小与口径相比属高阶小量。

把反射镜看成是由无数个微小单元组成的几何体，其在外力作用下处于平衡时，各个微元也应处于平衡，由此可建立反射镜的平衡微分方程

式中σx、σy、σz为镜面直角坐标系中x、y、z三个方向的正应力；τxy、τyz、τxz为三个方向的切应力；Fx、Fy、Fz为单位体积的单位力在三个方向的分量。另外，当反射镜处于弹性变形状态时，温度不变，应力和应变呈对应关系，将支撑力卸载后，支撑变形将消失。基于广义胡克定律，可建立各向同性完全弹性体的本构物理方程

式中εx、εy、εz为三个方向的正应变分量；γxy、γyz、γxz为三个方向的剪应变分量；E为反射镜材料的弹性模量；G为材料的切变模量。由于反射镜支撑变形是一个连续的过程，反射镜微元点位移也连续，可得出位移分量与各向应变的关系

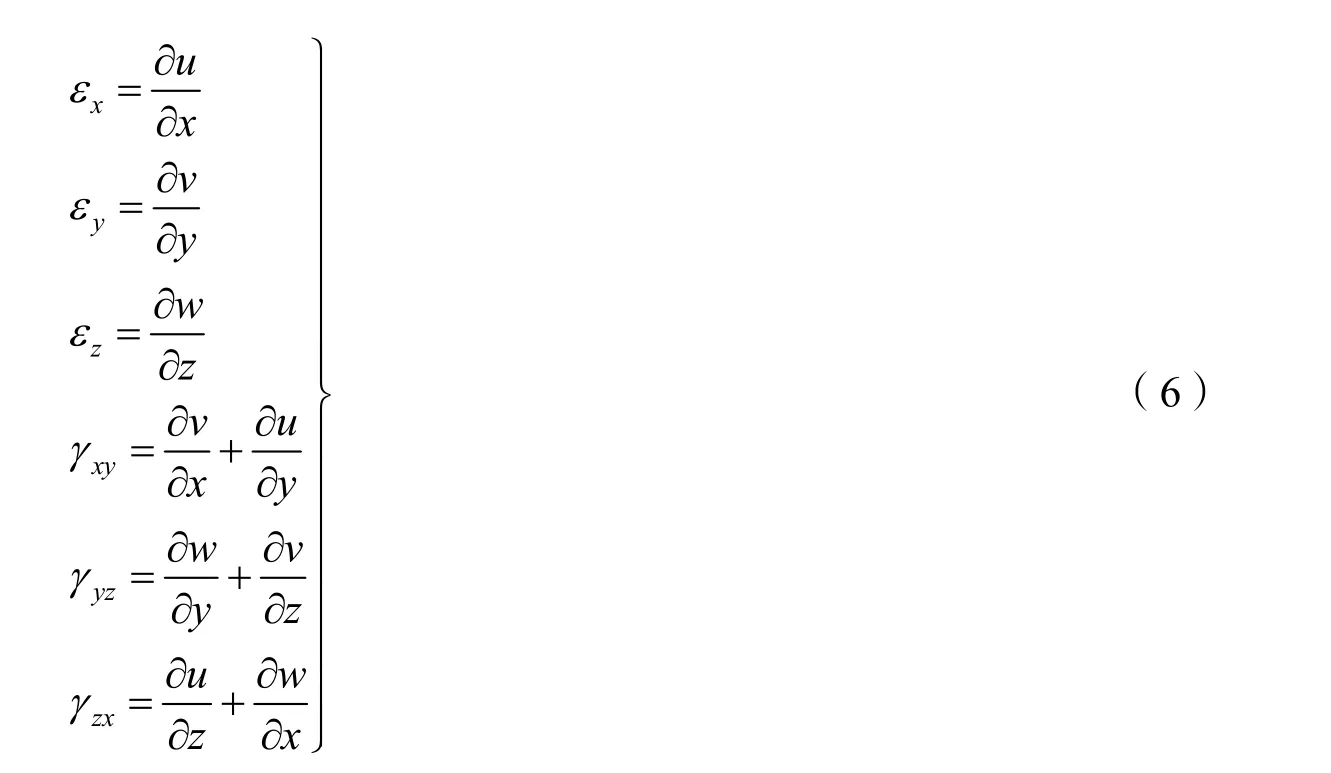
式中u、v、w为三个方向的位移分量。联立式（4）、（5）、（6）可得到15个方程。由反射镜力约束和位置约束，可得到力边界条件和位置边界条件，通过对上述微分方程组进行求解，可得相应支撑状态下的变形量大小。

在工程应用中，对微分方程组进行直接求解比较困难，计算此类问题多使用数值计算法，其中有限元分析法最为适用。

有限元法将反射镜当作一个集合，集合由相互连接的力学微元组成，反射镜整体力学特性由各微元的力学特性组合提供，集合中微元之间的内力由节点传递。当反射镜产生变形时，各微元也将变形，各节点形成相应位移。对每个微元设定一个函数，将节点位移作为未知量，建立节点内力与节点位移之间的关系，近似地表示微元内位移分布规律，对节点位移分量进行求解。集合上的位移场函数使用插值法求解，随着微元体积的减小、微元个数的增多，所求位移量的拟合程度将不断提高，最终在精确解处收敛。

通过对建立的反射镜有限元模型进行仿真，可得到相应支撑状态下的镜面支撑变形，该镜面变形中没有镜面加工残差。从变形云图中提取各点沿光轴方向的位移，进行泽尼克拟合，并将待测镜刚性位移部分去除，得到由支撑力产生的面形变化结果，进而建立偏差支撑力大小与面形变化量之间的关系，确定产生相应面形变化量的偏差支撑力大小。

3 试验验证与结果分析

使用某型号直径1300mm 的主镜进行误差分析方法的试验验证，该反射镜镜体结构如图1 所示，采用了ULE 材料的蜂窝夹心结构设计，轻量化率高达80%，面形为四次凹双曲面，顶点曲率半径R=3077mm，主镜有效通光口径为1300mm。

反射镜面形的检测光路由4D 干涉仪、球面波补偿器、折镜、重力卸载工装及主镜组成。为了减小干扰气流和环境温度导致的测量误差，对反射镜的测量环境进行了严格控制。

为了补偿反射镜的重力变形，采用了气压式多点浮动支撑的重力卸载方法。该支撑方式不引入附加力矩，因此面形结果中的镜面变形主要由支撑变形误差和加工残差两部分组成。经过有限元仿真优化后，采取了60个支撑点对反射镜进行支撑，使用7个气路进行控制，其中3个气路用于调整反射镜的倾斜。使用有限元分析得到了反射镜理论卸载情况下的面形变化峰谷值（PV）和RMS 值，如图2 所示。

图1 直径1300mm 非球面反射镜Fig.1 The aspheric mirror with diameter Ф1300mm

图2 理论卸载支撑变形Fig.2 Theoretical deformation with unloading support

由图2 可以看出，反射镜面形的理论卸载精度RMS 值为0.002λ，满足检测时的精度要求。反射镜专用的重力卸载装置主要由反射镜衬板、底板、气缸和控制系统等组成，如图3 所示。其中的衬板用于支撑反射镜；底板为气缸提供安装基准和接口；气缸用于对反射镜进行主动力支撑；配套的控制系统可以实现对不同气路气缸的独立控制。

图3 重力卸载装置Fig.3 The gravity unloading device

采用6 次旋转检测法对反射镜进行检测。在检测前，使用三坐标测量机在镜坯边缘处每隔60°进行了刻线，形成用于检测对准的6个标记。在使用干涉仪的检测过程中，以0°状态作为起始测量位置，利用干涉仪的校准功能，对检测光路和反射镜位置进行微调，使干涉仪图像的y轴与0°标记和180°标记重合，完成0°状态下的位置标定和面形检测。通过激光跟踪仪反馈反射镜的空间位置关系，以0°坐标值作为基准，进行等间隔60°旋转，每转过一个60°时，就重复上述步骤进行调整和跟踪仪标定。检测所采用的干涉仪角度误差为0.05°，可满足实际的检测精度需求。使用旋转检测法得到的6 次面形检测结果如图4 所示。

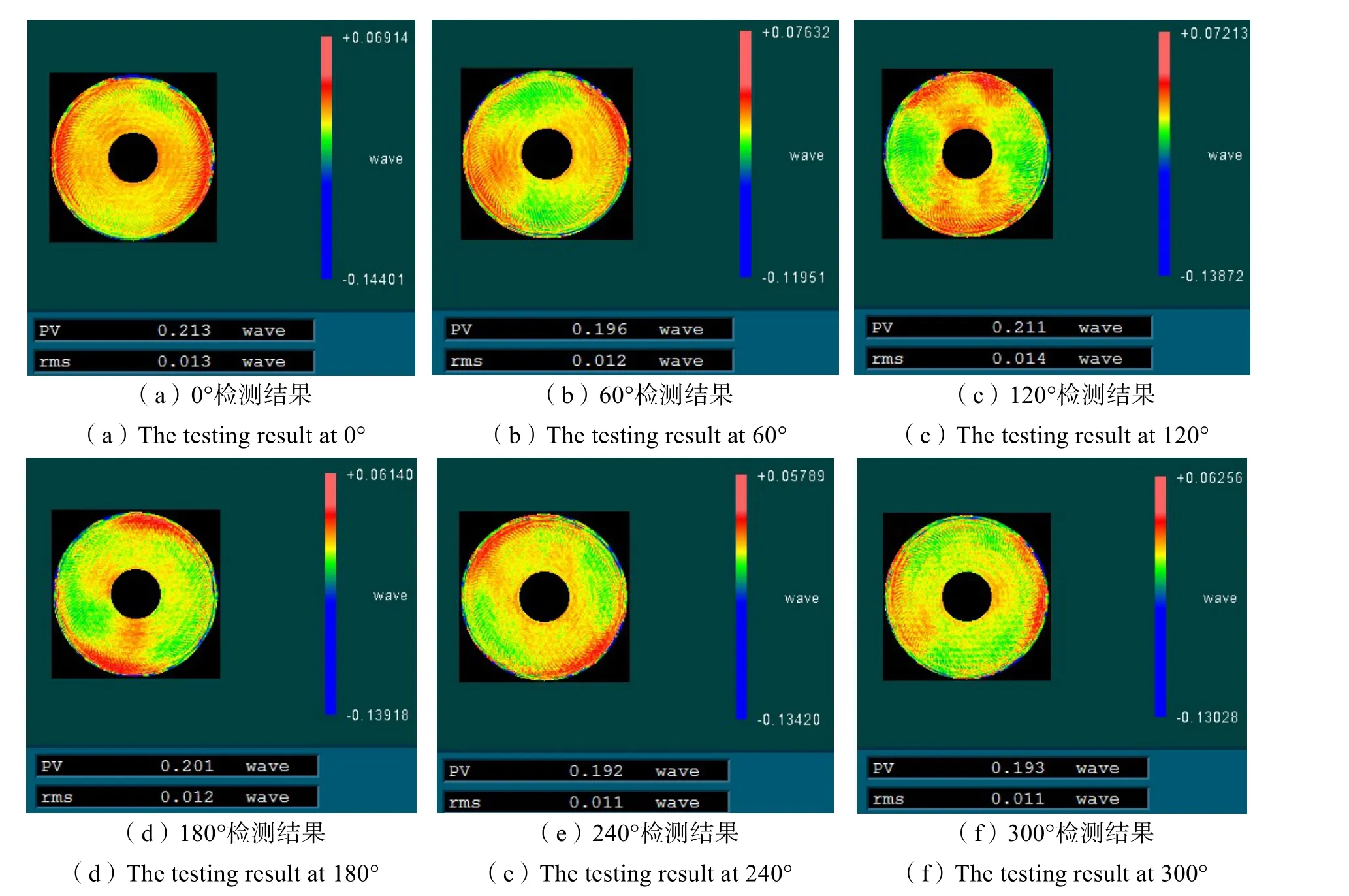
图4 旋转法面形检测结果Fig.4 Surface detection results by rotation testing

由图4 可以看出，各个角度下的面形检测结果稍有差异，这部分差异主要为支撑变形影响的结果。将6 次旋转检测所得面形结果使用干涉仪自带的软件算法处理后，得到检测结果的平均值，如图5 所示，该面形包含了支撑变形误差以及加工残差的算术平均值。使用泽尼克拟合，提取出中低频误差，即可得到该非球面反射镜的支撑变形误差，如图6 所示，支撑变形误差最大值为图6 中面形变化集中区域的面形变化峰值，为0.04970λ。

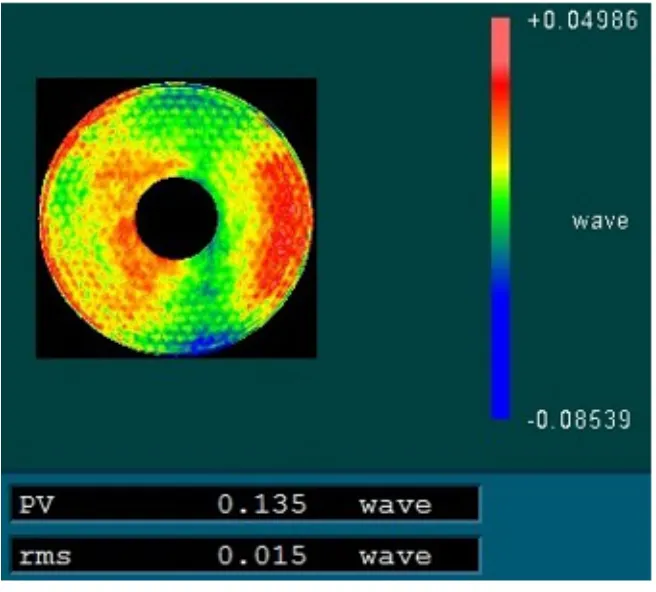
图5 检测结果平均值Fig.5 The average value of testing results

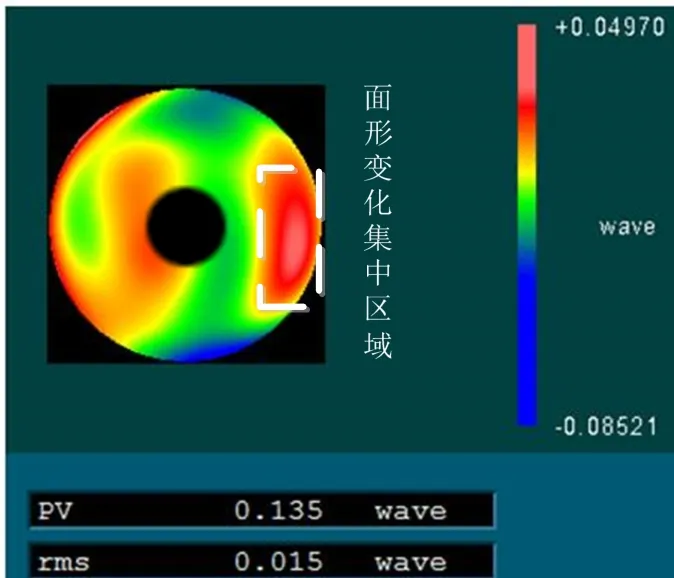
图6 支撑变形误差Fig.6 The support deformation error

对面形变化量的主要集中区域所包含的支撑点的支撑力误差进行分析。在实际检测时，该区域支撑点处施加的支撑力为16.2N。在此基础上，对支撑点施加额外的支撑力以表示偏差支撑力，支撑力大小相等，以1N 为跨度，由1N 变化到10N，由有限元仿真得到每一组力对应的镜面变形，通过软件去除刚性位移，得到面形变化结果。面形变化结果与施加偏差支撑力大小变化曲线如图7 中线a 所示。

与此同时，为了衡量有限元仿真精度与可靠性，使用直径1300mm 反射镜进行试验。镜面面形的刚性位移可通过软件算法进行去除，镜面加工残差部分在只改变支撑力大小时基本不变，因此可以将不同支撑力下测得的检测面形图使用干涉仪自带的软件算法进行相减，得到只由偏差支撑力变化引起的面形变化量大小。实验中在相同支撑点处施加等梯度偏差支撑力，以1N 为跨度从1N 变化为10N，得到的力与面形变化关系曲线如图7 中线b 所示，面形结果如图8 所示。

图7 有限元仿真的面形变化与实测面形结果Fig.7 Surface change curves of finite element simulation and measured results

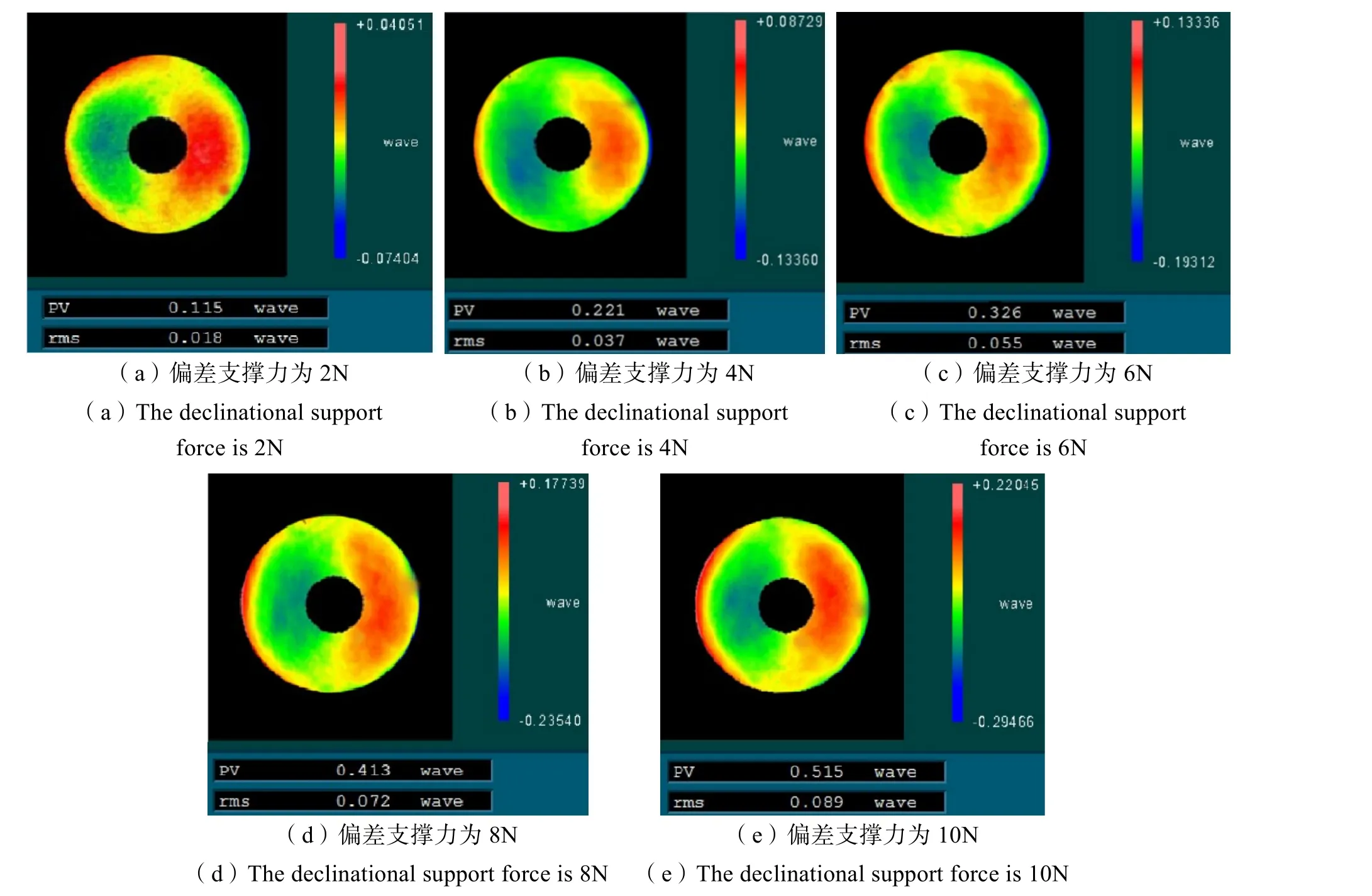
图8 不同偏差支撑力下的面形图Fig.8 Surface graphs under different deviation support forces

由图7 中曲线a、b 可知，当施加偏差支撑力大小从0N 加到10N时，有限元仿真得到的镜面理论变形量与实际面形检测结果都与偏差支撑力呈线性关系，但两条曲线斜率有一定差距。采用有限元模型计算得到的理论面形变化斜率Ka为

式中aWΔ 为采用有限元模型计算得到的理论面形变化量，ΔF为偏差支撑力大小。

反射镜实测得到的面形变化斜率Kb为

式中bWΔ 为反射镜实测得到的面形变化量。

在理想情况下，仿真得到的面形变化曲线应与实测曲线平行。然而受到模型边界约束条件、网格划分精度、结构尺寸误差等因素的影响，两条曲线很难呈平行关系。当偏差支撑力变化1N时，有限元模型仿真生成的面形变化和实验测得面形变化的差异为0.00485λ，导致二者产生较大差异的主要原因包括模型与实际反射镜的尺寸差、约束条件的设置、材料力学参数的设置、模型网格细分程度等。通过核对以上因素，发现自由度约束条件的设置是导致差异的主要原因，通过修正约束条件，将x、y方向的转动自由度约束由周边辅助约束点移到各支撑点上，这种约束方式与实际检测时更相符。重新进行有限元仿真计算，得到修正后的镜面变形结果与偏差支撑力大小关系曲线，如图7 中线c 所示。

修正模型后的理论面形变化斜率Kc为

式中cWΔ 为修正模型后的理论面形变化量。

当偏差支撑力变化1N时，此时理论面形变化和实测反射镜面形变化的差异为0.00187λ，该差异在镜面加工误差精度要求PV 值0.2λ 的1/100 以内，可以采用修正模型仿真得到的面形变化进行支撑变形误差分析。

由图7 中曲线c 可得，造成直径1300mm 反射镜支撑变形误差最大量0.04970λ 的偏差支撑力约为2.34N。若想使最大的支撑变形误差不超过0.03λ，则由曲线c 可知需要将偏差支撑力控制在1.38N 以内。该支撑力偏差的来源包括：气路气压控制误差、气缸促动器的输出力精度、底板定位孔的位置偏移等。在重力卸载方案的优化设计中，以1.38N 为指标，将该偏差支撑力分解到各部件上，如促动器的最大输出力精度误差ΔF不超过0.75N、气路气压控制误差产生的偏差支撑力不超过0.23N、由定位孔的位置偏移产生的偏差支撑力不超过0.4N。将前两项作为重力卸载装置中促动器、气压传感器、电磁阀等执行器件选型优化的依据，最后一项作为装置底板加工时的精度依据，结合有限元仿真分析，进行重力卸载方案的优化设计，若某部件指标精度难以实现，可以对偏差支撑力重新进行分配，调整各部件的指标大小，完成优化设计。最终，通过用滞后效应低控制精度高的薄膜式气缸代替原始的“O”型圈密封式气缸等执行器件、对底板定位孔的加工公差进行重新设计、使支撑点位置偏移最大误差不超过0.4mm 等方法，对重力卸载工装进行了优化设计与装调，并使用优化后的装置重新进行了直径1300mm 反射镜的检测试验，得到的6个角度检测结果如图9 所示，支撑变形误差如图10 所示。

通过对比图9 和图4 可以看出，优化装置后的检测结果PV 值变小；由图10 可以看出，支撑变形误差最大值减小为0.02871λ，这些结果都说明该方法对支撑变形误差最大值进行了有效地控制，这对实现大口径空间反射镜面形的高精度检测以及提高重力卸载工装的加工及装调精度都具有重要的意义。

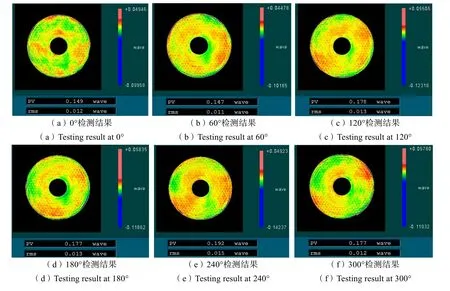
图9 优化装置后测得的面形检测结果Fig.9 Surface detection results after optimizing the device

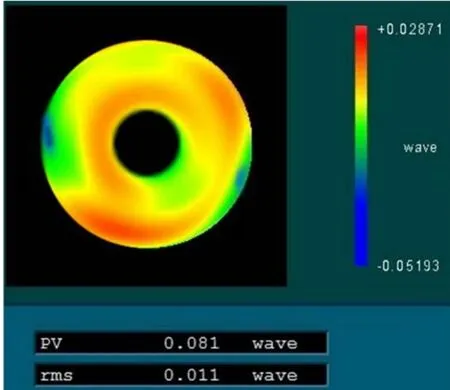
图10 优化装置后测得的支撑变形误差Fig.10 The support deformation error after optimizing the device

4 结束语

本文提出了一种应用于大口径空间反射镜检测过程的支撑变形误差分析方法。通过旋转法将支撑变形误差分离出来，由有限元分析方法建立偏差支撑力大小与面形变化量的关系曲线，以反射镜的实测面形建立有限元模型仿真精度判据，得到面形变化对应的偏差支撑力大小，并结合某型号直径1300mm 反射镜检测实例，验证了该方法的可行性，使高精度面形检测中的支撑变形误差分析成为可能。误差分析结果可用于对重力卸载装置进行选型优化，用以提供重力卸载工装的设计与装调，提高检测精度作参考。该误差分析方法不仅适用于米级口径，也适用于更大口径的空间反射镜高精度检测。接下来可以从支撑变形误差的精确控制角度开展研究，探寻有效减小支撑变形误差的方法。