IPMSM空载损耗受电压变化影响的仿真分析

张永平，段小丽，张翔宇，郭英桂

（晋中学院机械学院，山西晋中030619）

0 引言

永磁同步电动机（Permanent Magnet Synchronous Motor，PMSM）具有低损耗、高效率、高功率密度、高转矩密度、高功率因数等显著的优点，因而在纺织、机床、汽车、航空等许多行业或领域中获得了较为广泛的应用［1～3］.比如在纺织行业中，纺机设备中的梳棉机、精梳机、并条机、细纱机等配套使用永磁同步电动机，同时还要求机器具有较强的自起动能力，因而广泛采用设置有转子导条的内置式永磁同步电动机（Interior Permanent Magnet Synchronous Motor，IPMSM）.该类电机起动时，主要利用转子导条在气隙旋转磁场中产生的感应电动势，进而生成感应电流和电磁转矩，实现异步起动，同步运行的工作方式［4～5］.电机性能指标的优劣，是电机拖动负载能否满足工作要求的前提条件.电机在实际运行中，由于工作环境的变化、供电负荷的变化、电机负载的变化等各种因素的影响，使定子电压产生波动或变化，从而造成对电机性能的影响［6～8］.本文以细纱机配套使用的一款IPMSM为例，针对电机的空载稳态运行状态，应用MATLAB/Simulink提供的丰富的电力系统仿真分析工具，通过建立空载电流、各类损耗、效率等相关参数的数学模型，实现电压变化对IPMSM的空载损耗影响的仿真研究，通过与理论分析及电机空载试验数据相比较，说明本文分析的正确性与有效性，为IPMSM的设计或相关参数的优化提供一定的参考.

1 电机模型

图1为细纱机配套使用的一款IPMSM转子结构图.该电机的定子结构与异步电机类似，转子为凸极结构，四极电机，根据电机的凸极效应理论，电机设计时通过提高交轴同步电抗和直轴同步电抗的比值，提高凸极率，利用凸极效应产生的磁阻转矩提高电机的过载性能［9～10］，满足工作负荷要求，图2为细纱机工作时一个落纱过程的负荷曲线图.

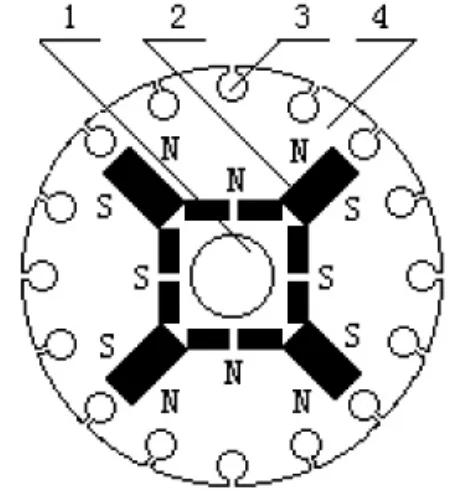
图1 内置式永磁同步电动机的转子结构图

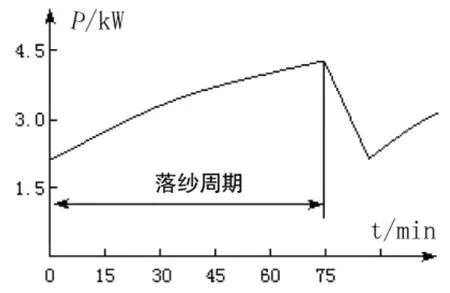
图2 细纱机落纱负荷曲线图

2 电压变化对空载特性影响的仿真分析

2.1 对空载电流的影响

2.1.1 数学模型

根据IPMSM的双轴反应理论，建立d-q轴坐标，则定子电压、定子电流及磁链等参数均可分解为相应的直轴分量和交轴分量，直轴磁链、交轴磁链的方程如下：

式（1）中，ψd-直轴磁链，ψ0-永磁体磁链；Ld-同步直轴电感；Id-直轴电流分量；ψq-交轴磁链；Lq-同步交轴电感；Iq-交轴电流分量.

根据磁链的数学模型，建立IPMSM在d-q轴坐标系下电压相量方程如下：

式（2）中，U-定子电压；Ud-直轴定子电压分量；Uq-交轴定子电压分量；Ra-定子绕组相电阻；E0-空载感应电势；Xd-直轴同步电抗；Xq-交轴同步电抗.

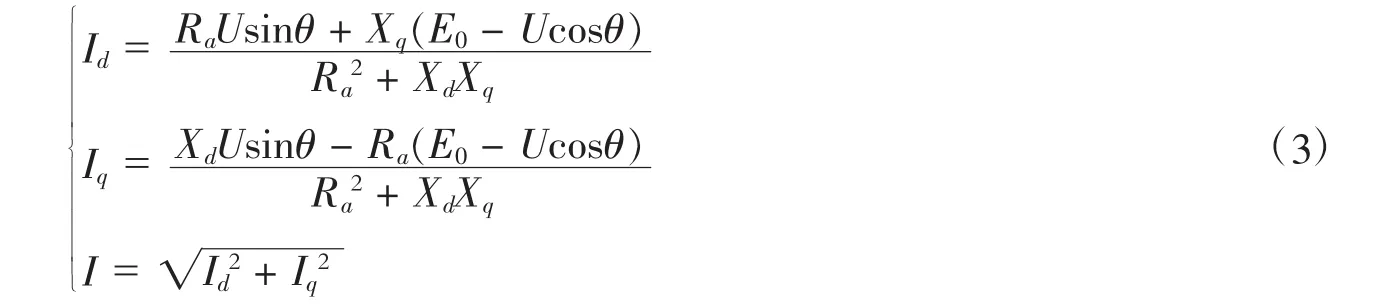
式（3）中，θ-功角，Usinθ=Ud，Ucosθ=Uq.

2.1.2 仿真实验

在MATLAB/Simulink环境下进行仿真研究.仿真采用图1结构电机，电机参数如下：额定电压值UN=380v，转速额定值nN=1500r/min，定子绕组相电阻Ra=1.732 Ω，直轴电感值Ld=2.37mH，交轴电感值Lq=5.68mH，永磁体磁链ψ0=0.187Wb，电机极对数p=2，定转子铁芯的硅钢片材料为35CS300.

由IPMSM理论可知：IPMSM在空载状态下，功角θ值非常小，当电压变化时，功角θ的变化量较小，当定子电阻Ra较小时，若忽略定子电阻Ra的影响，则式（3）可简化为下式：

根据IPMSM理论，当永磁体恒定时，E0为一常数.因功角θ值很小，则cosθ≈1，由（4）式可见，当电压增大时，直轴电流会减小，当电压增加到U＞E0时，直轴电流由正值变为负值；交轴电流与电压成正比，会随电压的增大而增大，但因sinθ非常小，可以认为交轴电流是一个很小的常数，图3的仿真结果与理论分析是吻合的.由式（3）可知，图3的交直轴电流叠加即为空载电流，是一条V型曲线（如图4所示），图4的仿真结果与表1的电机空载实验数据相吻合.

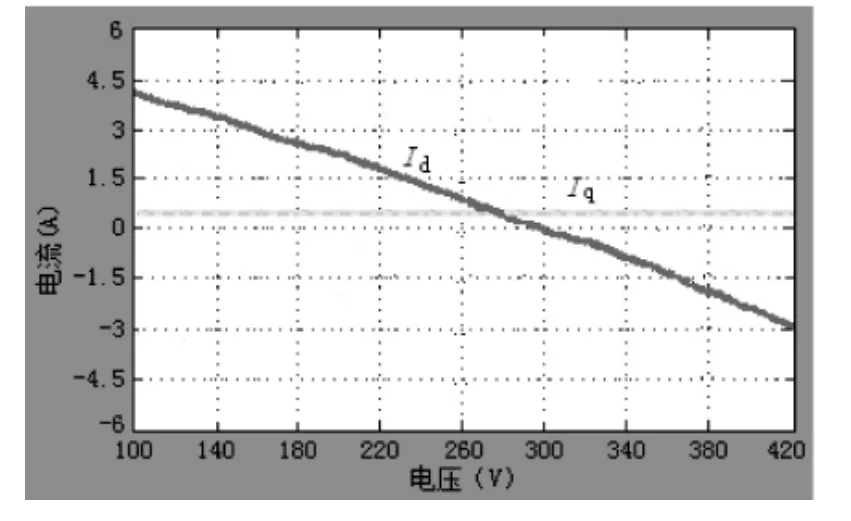
图3 交轴、直轴电流仿真波形图

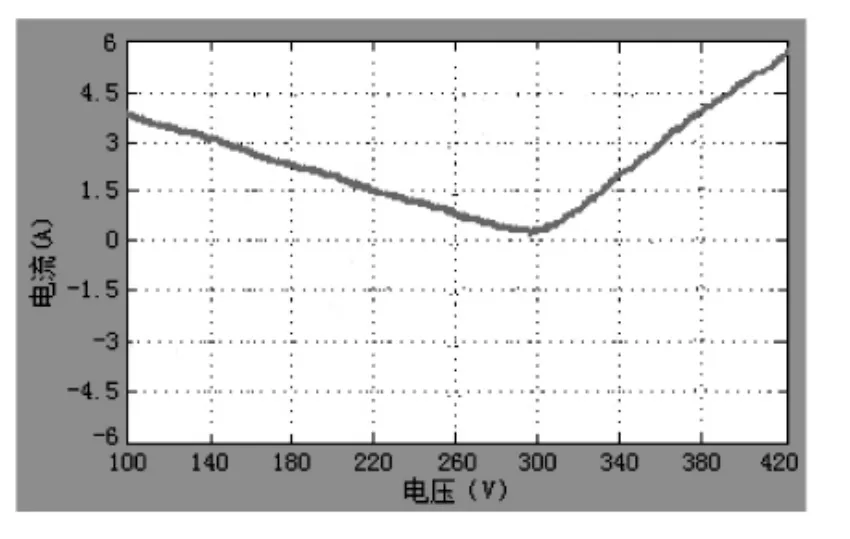
图4 空载电流仿真波形图

2.2 对空载损耗及效率的影响

电动机是将电能转换为机械能的装置.电机损耗的大小直接影响效率的高低，电机损耗一方面造成电能源的浪费，使电机运行效率降低，另一方面会造成电机温升的增高，过高的温升会影响电机的正常运行，甚至可能烧毁电机.IPMSM的损耗主要包括有铜损耗、铁损耗、机械损耗和杂散损耗等，IPMSM的各种损耗及其效率分析如下.

2.2.1 数学模型

1）铜损耗.IPMSM空载运行时，电流流过定子绕组产生的焦耳热称为定子铜损耗.因稳态时电机同步运行，转子导条中无感应电流，即稳态时转子导条不产生铜损耗.

式（5）中，Pcu-定子铜损耗.

2）铁损耗.铁损耗是电机铁心在磁化过程中磁畴不停地摩擦、振动所产生的消耗以及感应电流引起的发热损耗，它主要包括磁滞损耗和涡流损耗两部分［11～12］.

式（6）中，Pfe-铁损耗；Ph-磁滞耗；Pc-涡流耗；Kh-磁滞耗系数；Kc-涡流耗系数；Bm-最大磁密；f-交流电频率；Øm-最大磁通；kdq-绕组系数；N-定子绕组每相串联匝数.

对于铁损耗，因铁心所用硅钢片的磁导率为非常数，铁心中磁通与磁密的关系可根据铁心具体选用的材料查找其磁化曲线.

3）杂散损耗.杂散损耗也是一种在铁心中引起的损耗，又称为附加损耗.理论研究表明，杂散损耗主要是由高次谐波磁场及漏磁场等因素造成的，其与定子电流的方程如下：

式（7）中，Ps-杂散损耗；IN-额定电流；ks-杂散损耗系数；PN-额定功率.

4）机械损耗.电机运行时，电机产生的机械损耗主要取决于电机的结构、电机零部件的装配、部件间的配合及相互摩擦、传动机构等因素的影响，而与定子电压的变化没有关系.

5）效率.电机的效率是电机运行特性的一个重要指标，其关系到电机装置对取用电能利用率的高低，IPMSM相比同容量的异步电机效率高，是IPMSM获得广泛应用的原因之一.IPMSM的效率方程如下：

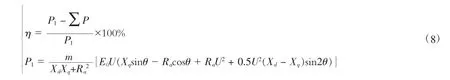
式（8）中，η-效率；P1-输入功率；ΣP-总损耗；m-电机相数.

2.2.2 仿真实验

应用MATLAB/Simulink进行仿真研究.图5-图7为各种损耗的仿真波形，图8为效率的仿真波形.图5的仿真结果显示，铁损耗特性是一条类似于双曲线的波形，这与表1的试验数据基本相吻合，同时IPMSM理论研究表明，电机的铁损耗与定子电压的平方近似成正比，说明图5的铁损耗仿真波形与电机理论相吻合；图6和图7的仿真结果显示，铜损耗和杂散损耗均是一条V形曲线，IPMSM理论表明，这两种损耗均与定子电流的平方近似成正比，可见仿真波形与电机理论相吻合，同时可以看出仿真波形与表1的试验数据也基本相吻合；图8的仿真显示，效率是一条倒V形曲线，与表1的试验数据相吻合.说明仿真分析的正确性与有效性.

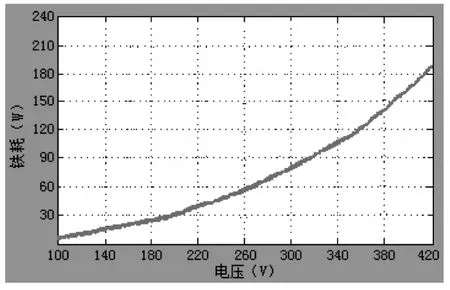
图5 铁损耗仿真波形图

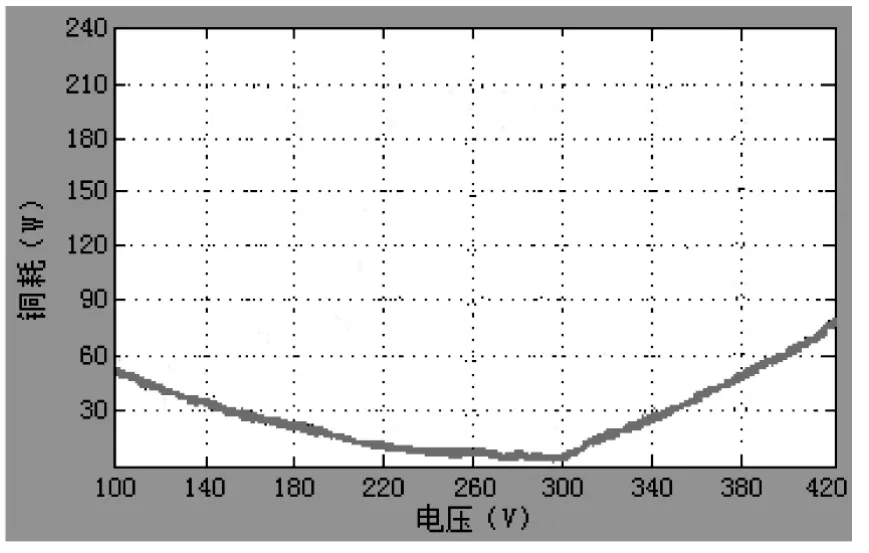
图6 铜损耗仿真波形图

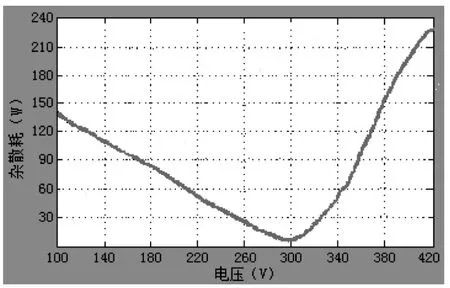
图7 杂散损耗仿真波形图

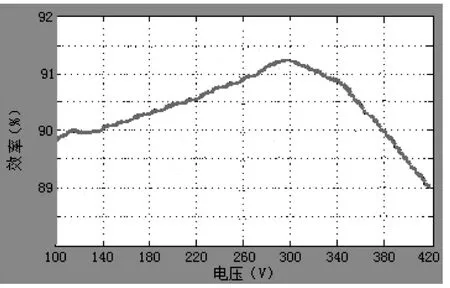
图8 效率仿真波形图

2.3 空载试验

将待测样机空载状态下运行，定子电压从高于额定电压逐步向下调节，注意电压不可调节的过低，以免过大的电流造成对电机的危害.实验时有关铁损耗、机械损耗、杂散损耗的分离方法参见文献［13］，空载试验数据如表1所示.

3 结语

IPMSM与同功率的异步电动机相比，因其优良的性能获得了日益广泛的应用，IPMSM的定子电压变化会影响电机的许多性能参数.本文以细纱机配套的一款IPMSM为例，建立相关性能参数的数学模型，应用MATLAB/Simulink电力系统仿真工具实现电压变化对IPMSM诸多空载损耗性能影响的仿真研究，仿真结果显示与IPMSM理论分析以及试验数据相吻合，表明仿真分析的正确性与有效性，为IPMSM的设计或参数的优化提供一定的参考.

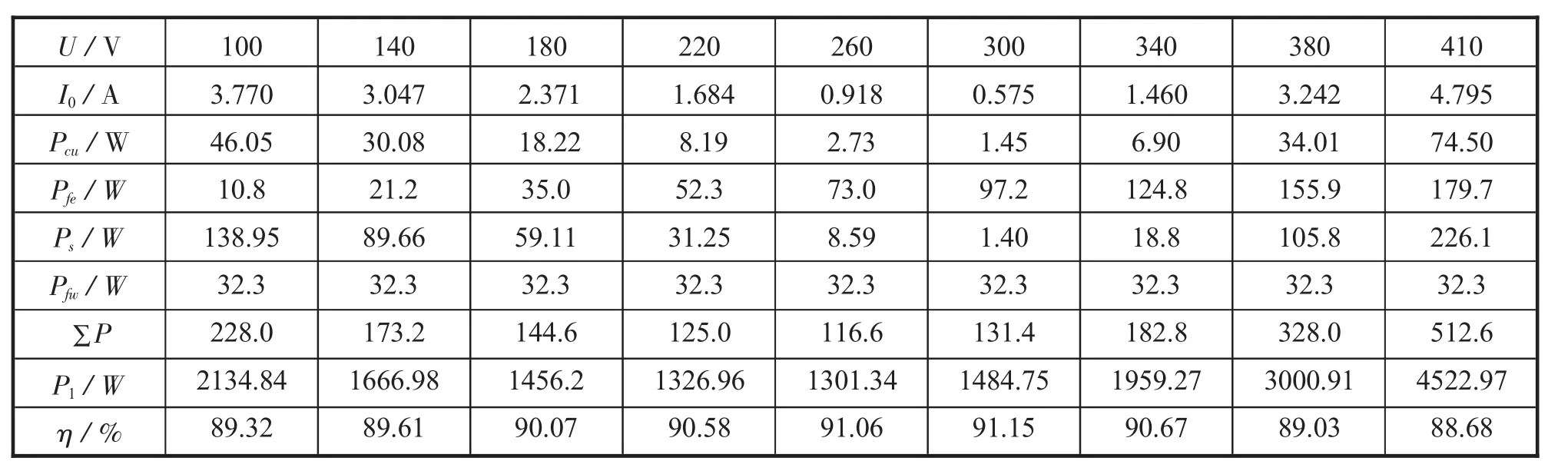
表1 电机空载试验数据表