单调有界定理的分析与应用

卢丑丽，周丽丽

（1.山西农业大学信息学院，山西太谷030800；2.晋中学院数学学院，山西晋中030619）

高等数学是大学大多数专业的必修课，主要培养学生的逻辑思维、辩证思维、理性思维能力，是高校重点学科之一.每年研究生入学考试高等数学所占比例至少为56%，高等数学的成绩决定了考研数学成绩的高低．高等数学的理论基础为极限，理解极限，学好极限，会求极限，学会举一反三，是学好高等数学的基础．单调有界定理是极限这一章节较为抽象的一个概念，但其应用较多，尤其成为考研数学、其他竞赛和选拔比赛练习中的热点．在高等数学教材中，给出单调有界定理如下：

单调有界数列收敛准则：单调增加有上界的数列必有极限；单调减少有下界的数列必有极限．

在高等数学教学过程中，数列极限常出现在极限准则部分，列举如下：

本文通过探究这类能运用单调有界定理求解数列极限的题目的共同之处，对其进行分析讨论，对数列极限的问题进行推广，得到以下一些命题.

类似的可以推广到以下推论：

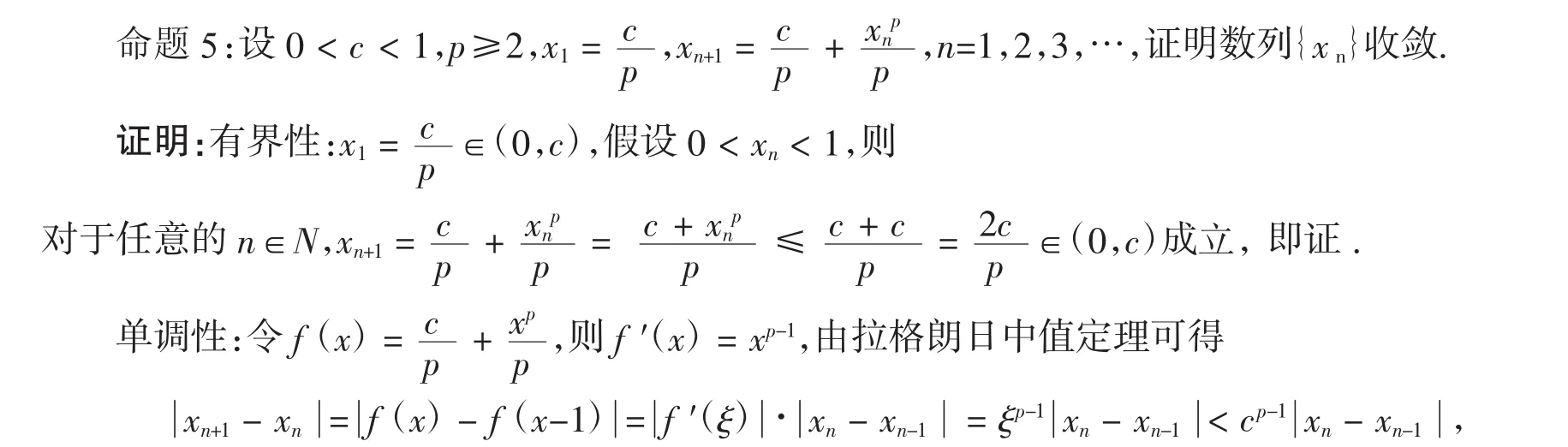
其中 ξ介于 xn与 xn-1之间，由于 0 ＜ c＜ 1，0 ＜ cp-1＜ 1，所以｛xn｝为压缩数列，则｛xn｝一定收敛，即证.

利用单调有界定理解题一般综合型较强，也是教学中学生容易混淆而不易理解的问题，本文中通过几个常见的特例加以说明，让学生在求极限时应注意与其他知识点相互联系，多思考，多动手，学会知识迁移，构建知识大网络，才能练就“下笔如有神”的真功夫.