《平均数》教学设计
2020-07-08
【教学内容】
人教版四年级下册第90~92页。
【教学目的】
1.初步理解平均数的意义,掌握求平均数的方法。
2.经历平均数概念的建立过程,培养观察、比较、分析、概括的能力。
3.体会平均数与生活实际的联系,增强学生应用数学的意识。
【教学重点】
正确理解平均数的意义。
【教学难点】
理解总数量与总份数的对应关系。
【教学过程】
一、创设情境,引入新课
师:“生命在于运动”。光明小学正在举行趣味运动会,同学们喝了不少矿泉水。雷锋小队收集了许多矿泉水瓶,让我们一起去看看吧!(出示课本主题图)
小红、小兰、小亮、小明分别收集了多少个?(14、12、11、15)
班主任张老师提出了一个问题:“你们小队平均每人收集了多少个?”
师:你能解释一下什么叫“平均”吗?
预设:一样多、公平……
(根据学生的回答,教师板书课题:平均数)
师:你们听说过平均数吗?今天这节课我们就来研究《平均数》。看了这个课题,你想知道平均数的哪些知识呢?
【设计意图:灵活运用课本主题图,创设学校召开运动会的情境,自然巧妙地引入新课。特别是让学生自主提问,开放了课堂,发散了思维,同时也明确了本课的学习目标。】
二、自主探索,建构意义
1.探索平均数的求法。
师:班主任张老师提出的问题“雷锋小队平均每人收集多少个”,你们会解决吗?
(学生独立思考,汇报交流)
(1)把多的补给少的。
师:(追问)你能给这种方法起个名字吗?
预设:取长补短、移多补少。
(2)列除法算式计算。
师:(追问)括号里求的是什么?为什么要除以4?你也能给这种方法起个名字吗?
预设:括号里求的是4个人收集的矿泉水瓶总个数,因为是4个人,平均分成4份,所以要除以4。先加后除、先合后分…
【设计意图:让学生根据自己已有的知识经验去创造平均数的求法,给学生提供了更大的思维空间。】
2.初步理解平均数的意义。
师:通过移多补少或先合后分的方法得出4个人的平均数是13,是不是每个人实际上都收集了13个瓶子?
(学生观察、讨论,得出平均数不是一个实际的数,而是一个虚拟的数)
师:平均数13与原来4个数据14、12、11、15相比,你发现了什么?
(平均数比最大的数小、比最小的数大)
师:平均数为什么比最大的数小、比最小的数大呢?
(学生讨论得出:平均数是移多补少得来的,所以它不可能比最大数大,也不可能比最小数小,处在最大数与最小数之间)
【设计意图:三个问题层层递进,步步紧逼。学生的思维拾级而上,顺利地建构了平均数的初步意义。】
3.加深理解平均数的意义。
师:了解了雷锋小队收集矿泉水瓶的情况,我们再来看看踢毽小队的比赛情况。
(1)人数相等。
(课件出示)

男生组 女生组姓名 踢毽个数 姓名 踢毽个数王小飞 19 杨 羽 18刘 东 15 曾诗涵 20李 雷 16 李 玲 19谢明明 20 张 倩 19
师:哪个组成绩好?只要比什么就行了?
(女生组,比踢毽的总个数)
(2)人数不等。
师:现在男生组再补一个选手“孙奇”踢了15个。
(教师在对应的算式中加上15,形成算式19+15+16+20+15=85),现在男生踢毽总个数是85,男生成绩好)
①引起矛盾——不公平。
师:为什么不公平?那该怎么办?
(学生讨论得出:人数不相等时比较踢毽总个数是不公平的,可以让女生组再添一名选手)
②激化矛盾。
师:如果就是不让女生再添一名选手,难道就不能赛出冠亚军吗?这时候该怎样比较出两个组比赛的水平呢?
(学生小组讨论,一致认为用平均数来比较)
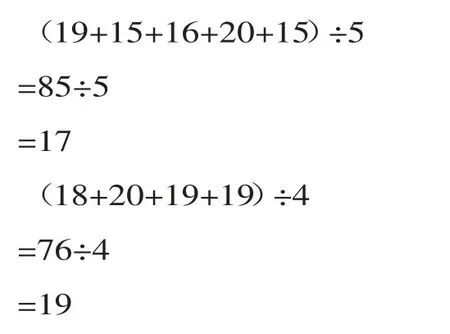
师:平均数17、19是男生组、女生组里各个选手的实际个数吗?由此发现,平均数能反映出各组的实际水平吗?
(平均数虽不能反映一组数据的实际水平,但可以反映整体水平)
(板书:整体水平)
教师小结:平均数虽然是虚拟的,不是实际的,但可以较好地帮助人们解决生活实际中的公平与否问题,这就是平均数在统计学中的作用。
【设计意图:对例题进行创造性地处理,即拆分为两种情况——人数相等和人数不等,设置思维的障碍,激起矛盾的冲突,让学生产生强烈的学习需求,感悟用平均数来比较的必要性与公平性,加深对平均数统计意义的理解。】
三、反馈练习,拓展应用
师:下面我们再去运动会上看看50米跑的情况:
课件出示:

姓名 杨欣宇 王波 刘真尧 马丽 唐小东时间 8秒 10秒 9秒 12秒 11秒
1.你能估计一下这5个人平均每人跑了多少秒吗?
2.你们的估计准不准呢?能用自己喜欢的方法验证一下吗?
(学生独立思考,汇报交流。有的用移多补少,有的用算式计算,有的去掉最大数与最小数后再计算或移多补少)
【设计意图:让学生估一估平均数进而验证估计是否准确,学生势必在头脑中进行信息的筛选、调试与加工,既促进思维能力的发展,又培养良好的数感与验算的习惯。】
师:我们再去运动会上看看选手们的投篮情况:
第一场投中27个,第二场投中23个,第三场上半场投中12个、下半场投中16个,平均每场投中几个篮球?
A.(27+23+12+16)÷4
B.(27+23+12+16)÷3
学生判断得出正确答案B后教师提问:如果答案A是正确的,那么题目该怎样改变?
预设:把第三场投中个数定为12个,第四场投中个数定为16个。
【设计意图:第三场篮球投中的个数没有直接给出,这样可以消除学生“被除数中有4个部分量,除数就是4”的思维定势。同时教师的追问,从反面强化学生对“总数量”与“总份数”对应关系的正确认识,切实把习题用足、用透。】
师:最后我们去运动会看看平板支撑的比赛情况:
平板支撑的队员平均身高148厘米,150厘米长的海绵垫一定能使每名队员撑得下吗?
学生讨论:148厘米是平均身高,是一组队员的整体水平,队员的实际身高有的要小于148厘米,有的大于148厘米,还有的甚至大于150厘米,所以150厘米长的海绵垫不一定能使每名队员撑得下。
【设计意图:通过“平均身高148厘米”与“150厘米长的海绵垫”的比较,可以极大地激发学生思维的积极性,进一步促进学生对平均数意义的深度理解,培养学生运用所学知识解决实际问题的能力。】
四、全课总结,升华认识
1.说一说平均数到底是一个什么样的数?它能解决现实生活中的什么问题?
2.平均数能解决现实生活中的公平与不公平的问题,那么平均数是不是就一定最公平、最合理呢?比如,甲的月工资是8000元,乙的月工资是800元,甲、乙两人月平均工资是4400元,此时的平均数你们觉得怎么样?这个问题留给大家课后思考。
【设计意图:在学生对平均数知识整理的基础上教师又抛出一问,巧妙地激发学生的学习兴趣,引发学生的思维再次起航,从而对平均数的认识更全面、更科学,收到“课结束、趣仍在、思犹浓”的教学效果。】
