“假”戏真做 弄“假”成真——《鸡兔同笼》教学设计（一）

【教学内容】

北师大版五年级上册第99、100页《尝试与猜测》。

【教学过程】

一、找准起点，从假设出发

1．微课学习，效果反馈。

师：课前通过观看《鸡兔同笼》微课，你们有什么收获？

（微课介绍了鸡兔同笼问题，和逐一列表法）

预设：知道了什么是鸡兔同笼问题，学会了列表法可以解决这个问题。

2．展示作品，体会假设。

鸡兔同笼，有9个头，26条腿，鸡、兔各有几只？

师：请同学们拿出昨天发的微课《学习任务单》，说一说你是怎么填写的？

预设：

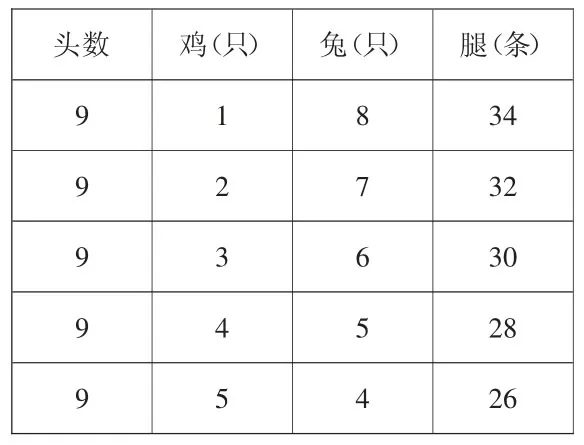
头数 鸡（只）兔（只）腿（条）9 1 8 34 9 2 7 32 9 3 6 30 9 4 5 28 9 5 4 26

师：你是怎么想的？这个表格是什么意思？

预设：假设鸡是1只，那兔就是8只，腿一共是34条；假设鸡是2只，那兔就是7只，腿一共是32条；……

师：是的，通过逐一假设，并借助表格很快找到了正确答案。

【设计意图：五年级的学生已有列表解决问题的初步经验，利用微课，把数学课堂延伸至课外，让学生自主尝试，初步认识鸡兔同笼问题，确定用列表法解决简单鸡兔同笼问题的基本策略，渗透假设的思想，为课堂学习做好知识和活动经验上的铺垫。】

二、立足假设，引导主动探究

●探究活动一：利用表格，寻找规律。

师：观察表格，你发现了什么？（学生独立思考，小组交流，全班汇报）

预设1：鸡的只数在增加，兔的只数在减少，腿的条数也随着减少。

预设2：鸡的只数每次增加1只，兔的只数就减少1只，腿的条数就减少2条。

师：为什么腿的条数会减少2条？

预设：兔比鸡多2条腿，1只兔换成1只鸡就少了2条腿。

师：换1只，总腿数减少2条，如果再换1只呢？再换1只呢？……

师：按照这种方法一直换下去，离实际的腿数越来越近，是不是一定能找到答案呢？

预设：是的。

●探究活动二：再次尝试，激发简化需求。

出示《孙子算经》原题：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？

1.尝试逐一，体验繁琐。

（1）学生分组尝试填写。

（2）学生汇报，说一说填写的过程。

预设：

?

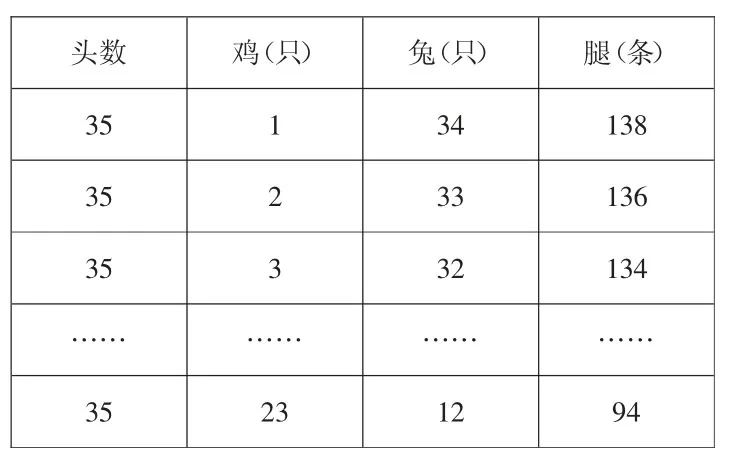
师：腿的条数是怎么算的？

预设：鸡的只数×2+兔的只数×4＝腿的总条数。

师：你们是不是每一栏都用这种方法算腿的条数的？

预设：不需要每一栏都算，我是算出第一栏一共是138条，后一栏就少2条，每增加1只鸡，腿的条数就减少2条。

师：填写完了这个表格，你有什么感受？

预设：太麻烦了。

师：是啊，整整列了23 行，想一想，能不能想到什么办法让列表的过程再简单些？

【设计意图：逐一列表法是解决鸡兔同笼问题的一种最基本的方法，让学生再次巩固应用逐一列表法，使全体学生都能熟练地掌握逐一列表法解决鸡兔同笼问题。此例题的数据较微课中例题数据更大，计算难度和列表过程更加繁琐，使学生体会到随着数据的增大，逐一列表法的劣势更明显，从而产生进一步简化的心理需求。】

2.尝试跳跃，化繁为简。

（1）学生分组讨论后尝试。

（2）汇报发现。

?

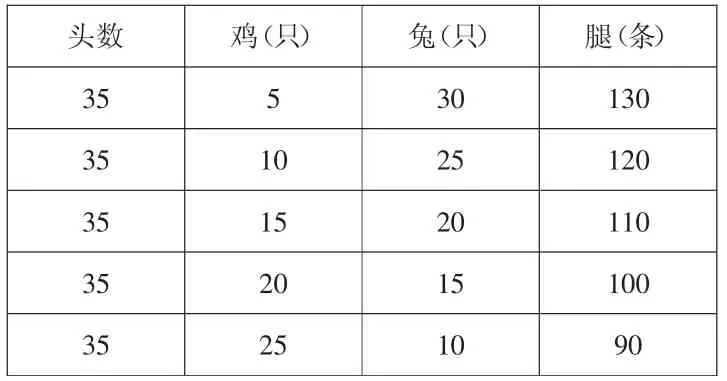
师：介绍一下你们这样列表的过程，说说你们的想法。

预设1：我觉得一次换1只太麻烦，我就一次换2只，这样一次就减少4条腿，总腿数离实际腿数越来越近。

预设2：换2只还是太麻烦，我一次直接换5只，这样一次腿就少10条，这样会找得更快!

（根据学生的回答引导学生发现，在跳跃的过程中，根据假设后算出的腿数与实际腿数之间的差距，进行调整，腿数多要减少兔的只数，反之则增加兔的只数，逐步逼近正确结果，在这一过程中注意引导发现折中列表法）

3.尝试折中，再次优化。

师：既然可以一次调整2只、5只，那我们可不可以再大胆一些，一次调整一半？（逐行出示下表）

?

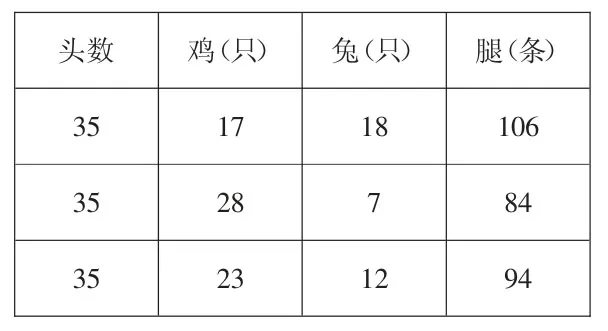
（引导学生填写出上表，重点让学生说一说，根据上行数据结果，该往什么方向调整才能找出正确的答案）

师：这种跳跃列表（折中列表）的方法和逐一列表的方法比较，有什么好处？

预设：减少了列举次数，更快地找到正确答案。

师：刚才我们学会了列表解决问题，但列表法总是有些麻烦。大家想一想，如果数据再大一些，这种方法怎么样？还有没有其他方法呢？

【设计意图：充分尊重学生的思考过程，在表格的对比中，逐步简化列表过程，让学生体会其中的规律，引导意会鸡或兔的只数变化与腿数变化之间的规律，为后面的计算方法解决问题埋下伏笔。】

●探究活动三：再探规律，拓展延伸。

师：从刚才的列表法中，我们发现了很多规律，能不能利用这些规律找出更简捷的方法？

1.再现逐一列表。

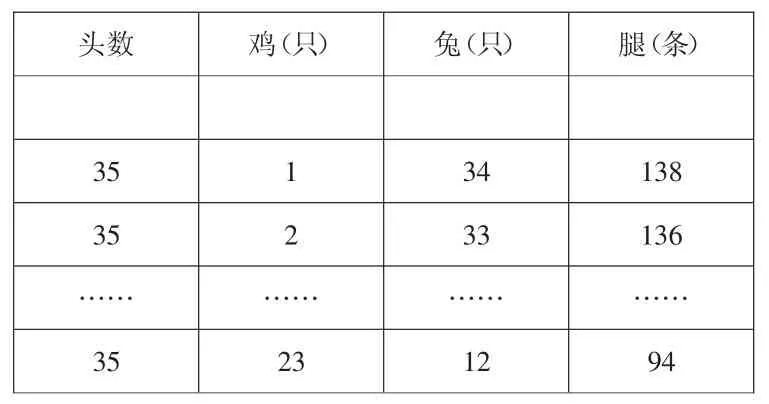
头数 鸡（只）兔（只）腿（条）35 1 34 138 35 2 33 136…… …… …… ……35 23 12 94

师：如果让你把第一栏填完整，怎么填写？

预设：35 0 35 140。

师：第一栏什么意思？

预设：假设鸡是0只，兔就是35只，腿一共是140条。

师：也就是假设全部是兔，腿一共有140条。

2.再探规律，沟通联系。

师：从上表中，你能发现哪些规律？

预设：总头数不变，鸡的只数在依次增加，兔的只数依次减少，腿的条数依次减少2条……

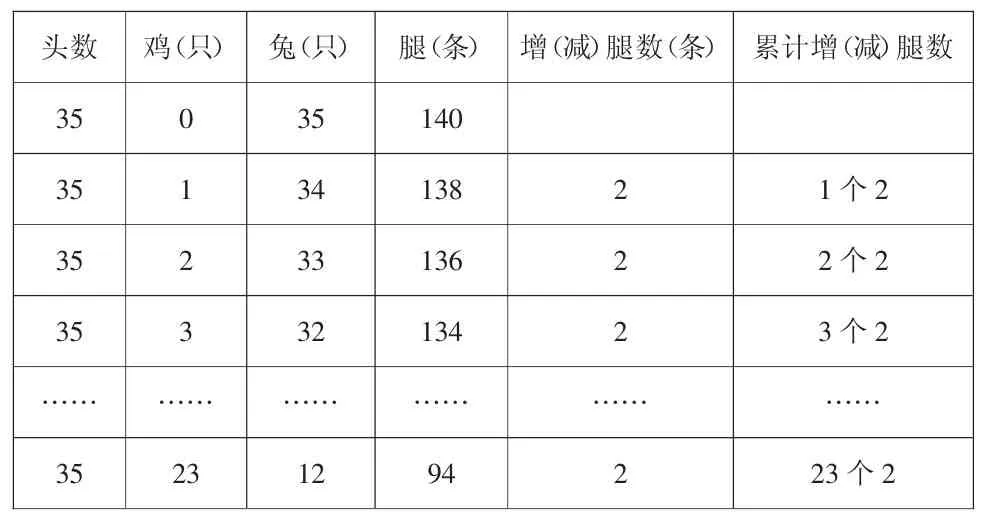
头数 鸡（只）兔（只）35 0 35 35 1 34 35 2 33 35 3 32…… …… ……35 23 12腿（条）140 138 136 134……94增（减）腿数（条）累计增（减）腿数2 2 2 …… 2 1个2 2个2 3个2……23个2

根据学生的回答，课件依次展示上表后两列。

预设：鸡的只数每次增加1只，兔的只数就减少1只，腿的条数就减少2条。

师：也就是用1只鸡换掉1只兔，腿的条数就会减少2条，反之用兔换鸡就会增加2条。

师：从假设是0只鸡到23只鸡，腿的条数累计减少了多少？

预设：2×23=46（条），也就是23个2。

师：这个算式每个部分表示什么？可以得到什么样的数量关系？（小组讨论后汇报）

预设：2是1只鸡兔的腿数差，23是鸡的实际只数，46表示假设鸡是0时总腿数与实际腿数之间的差。

鸡的实际只数×2=假设的总腿数－实际腿数

（假设的总腿数－实际腿数）÷2=鸡的实际只数

师：那是不是说，只要知道了假设后的总腿数与实际腿数的差就能算出鸡的只数？（将上表改为下表显示）

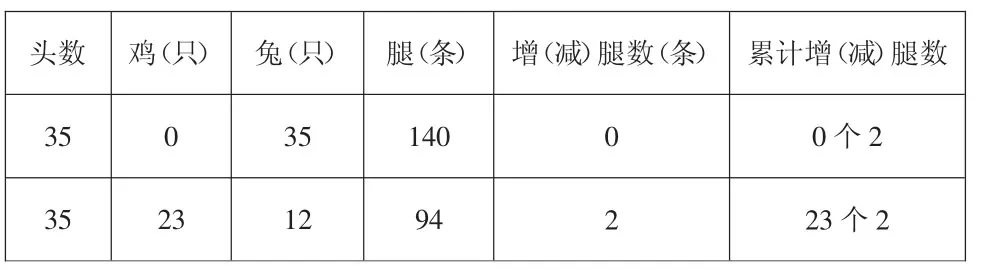
头数 鸡（只）兔（只）腿（条）增（减）腿数（条）累计增（减）腿数35 0 35 140 0个2 35 23 12 94 0 2 23个2

师：你怎么算？

预设：假设全部是兔。

鸡的实际只数：（35×4-94）÷2=23（只）

兔的实际只数：35－23=12（只）

师：为什么这么算？

引导学生总结：假设全部是兔，（兔的只数×4-实际总腿数）÷2＝鸡的实际只数，总只数－鸡的实际只数＝兔的实际只数。

师：既然假设全部是兔，那可不可以假设全部是鸡呢？

预设：假设全部是鸡。

兔的实际只数：（94－35×2）÷2=12（只）

鸡的实际只数：35－12=23（只）

师：你是怎么想的？

引导学生总结：假设全部是鸡，（实际总腿数-鸡的只数×2）÷2＝兔的实际只数，总只数－兔的实际只数＝鸡的实际只数。

小结：假设全部是鸡，或全部是兔，根据假设之后的腿数与实际腿数之间的差，我们就能推算出鸡或者兔的实际只数了，这种方法就是假设法。

【设计意图：在列表的基础上，通过比较，引导学生发现表格各项之间的变化规律，进一步的思考，运用逆向思维，从表格累计增减腿数反推到：只要知道假设的总腿数与实际腿数差就能求出鸡的实际只数，水到渠成。假设法计算与列表法虽同属假设，但在解决问题的效率上更胜一筹，为学有余力的学生提供了更多的解题策略。】

三、巩固应用，拓展视野

1.有龟和鹤共40只，龟的腿和鹤的腿一共有112条，龟和鹤各有几只？

师：我国的鸡兔同笼问题传到日本就变成了龟鹤问题，请你从列表法和假设法中任选一种，解决这个问题。

（学生独立完成，集体汇报）

2.全班一共有38人，共租了8条船，已知每条大船限乘6人，每条小船限乘4人，大小船各租了多少条？

师：这个问题虽然和鸡与兔没有直接的关系，但解决问题的策略却是一模一样的，也是通过假设来解决问题，这种问题也属于鸡兔同笼问题。

3.课后查一查资料，鸡兔同笼问题还有哪些解法？生活中还有哪些问题也是鸡兔同笼问题？

【设计意图：通过各种不同类型的鸡兔同笼问题练习，让学生在生活中找一找鸡兔同笼问题，让学生知道鸡兔同笼问题是系列问题，用假设的思考方法可以解决系列问题，把知识转化为一种解决问题的能力。】