巧设情境，理解平均数的统计意义——《平均数》教学实践及反思

《平均数》是人教版四年级下册的教学内容，这一内容属于“统计与概率”的学习领域。平均数是统计中的一个重要概念，它反映的是一组数据的集中趋势，代表了一组数据的整体水平。本节课是学生第一次接触平均数，学生理解平均数的意义尤为重要，而平均数的意义理解一般有三个方面：概念意义、算法意义和统计意义。在以往的教学中我们对于平均数算法及平均数概念研究得较多，常常将平均数作为一项技能教学，但关注平均数的统计意义较少。基于上述分析，确定本节课的目标如下：

1.经历数据统计和分析的过程，感受求平均数的实际需求，感知平均数的统计意义，构建平均数的概念，理解和掌握简单的求平均数的方法。

2.在运用平均数的知识解释简单的生活现象过程中，培养初步的统计意识和数据分析能力。

3.了解平均数在现实生活中的应用，感知数学与生活的密切联系。

【教学过程】

一、问题情境，引出平均数

1.情境导入。

师：今天，我们将跟随着主人公朱迪一起走进奥运村。看看在这里又有什么样的数学问题等着我们去发现、去解决。

2.问题解决。

（1）出示情境一，提出问题。

师：在这里她和尼克进行了一场投篮比赛。朱迪和尼克的投篮次数、成绩如下。

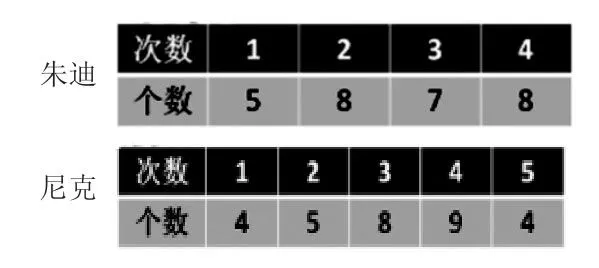
（2）独立思考。

师：你觉得朱迪和尼克谁投得更准一些？你是怎么想的？

（3）全班交流。

生：算出朱迪投篮总数28个和尼克投篮总数30个。因此，尼克比朱迪准。（板书：总数）

生：我认为尼克投了5次，朱迪投了4次，这样比不公平。

生：我觉得算出他们的“平均数”来进行比较。朱迪平均每次投了（5+8+7+8）÷4=7（个）；尼克平均每次投了（4+5+8+9+4）÷5=6（个）；7＞6，所以朱迪更准一些。

师：谁还想说？

生：我同意他的说法，这样可以求出他平均每次投了几个，不受次数的影响。（板书：次数）

师：你同意他们的想法吗？

（4）体会平均数的优越性。

师：看来同学们更同意比较平均数而不是总数。因为它不受次数的影响，比的是平均的水平。

3.揭示课题。

师：今天，我们学习的内容就与平均数有关。刚才，他是怎么得到平均数的？

生：总数÷次数=平均个数。

【设计意图：以学生比较熟悉的情境导入，自然引出投篮比赛。“你觉得朱迪和尼克谁投得更准一些？你是怎么想的？”在讨论后，学生感受到在总数与次数都不相同的情况下，需要产生一个新的量来衡量它们的水平。根据学生原有的生活经验，学生想到计算平均数来比较。这时他们对平均数的理解仅仅停留在计算的意义方面。】

二、理解平均数的统计意义

1.数形结合理解平均数。

（1）在实物图中理解平均数。

①用实物图表示。（感受总数、次数）

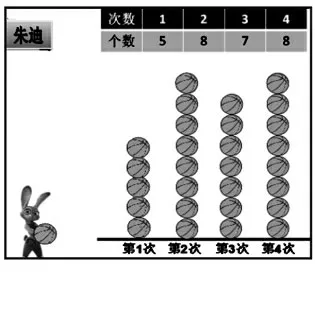
师：平均每次投了7个，如果我用一个篮球表示它投中的个数，那么第1次投中了5个，谁愿意上来移一移？第2次、第3次、第4次能想象吗？（出示所有实物图）

②独立思考。（感受平均数）

师：平均7个？怎么理解？谁能让其他同学看得更明白？

③全班交流。

生：我分别从第2次、第4次中的8个中移1个到第1次中，那么四次的投篮次数相等，都是7个。平均7个。

生：我是这么想的：我先看！发现第1次最少，第2次、第4次最多。于是我想能不能把第2、4次的篮球移到少的地方。发现刚好都是7个，平均7个。

生：这两位同学的方法是一样的，但是第二位同学先观察多少，再移这样的方法更好！

师：是的！把多的移到少的地方。这样的方法称为：移多补少。

④对比提升。

师：看来可以通过移多补少、计算的方法得到平均数。我们可以说7是5、8、7、8的平均数。

（2）在统计图中理解平均数。

师：用一个篮球可以很形象地表示他投中的次数。当然也可以用长方形的高度表示。

①第一步：出示统计图。

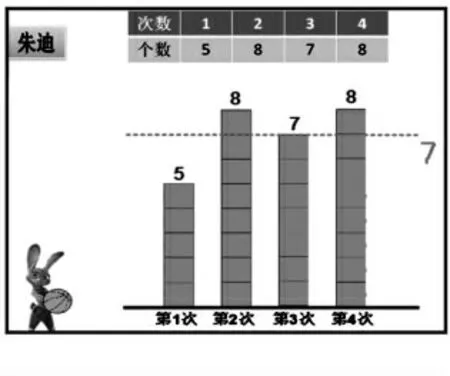
②第二步：先出示竖轴和刻度，再对应的出示数据，最后用红点标注平均数。

师：能想象刚才移的过程吗？

（3）小结。

师：这里两个7表示的意思一样吗？还能想象平均数的位置吗？说一说谁是谁的平均数。

2.感受平均数的统计意义。

（1）平均数是一个统计量。

①提出问题。

师：在回去的路上她碰到了要去参加跳水比赛的夏齐羊。你又能提出哪些与平均数有关的问题？

生：它们的平均身高是多少？

②解决问题。

师：你是怎么想的？

生：如果把高的一部分平均分成两份，一份移给朱迪，那么两人就一样高了。（边说边演示）

生：还可以把他们俩的身高相加，再除以2。

③小结。

师：很好，这样的身高是她的身高吗？是的，这是一个统计量，不是具体的量。

（2）最小值＜平均数＜最大值。

①出示情境，提出问题。

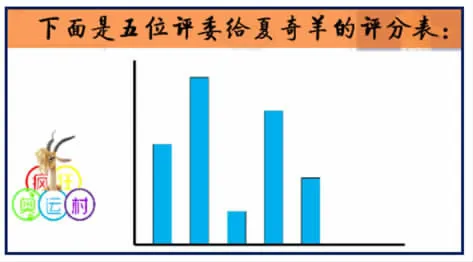
师：来看夏齐羊的第一跳。上图是五位评委给她的评分。根据条形统计图，你能估计出这组数据的平均数位置吗？三位同学是如下这样想的，你有什么想说的？

②全班交流。

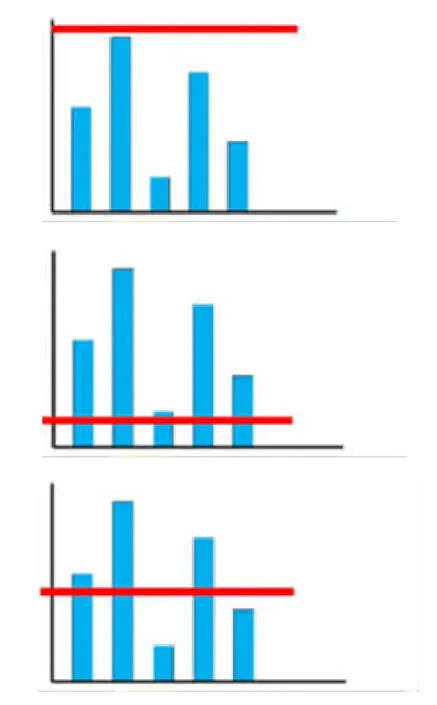
生：我觉得第一幅和第二幅肯定不可能。怎么可能平均数比最大的要大，比最小的还要小。如果这样的话，移多补少谁移给它呢？根本不可能。

师：看来估平均数是有范围的。（板书：最小值＜平均数＜最大值）

③验证。（出示数据分别是：6、10、2、8、4）

（3）平均数受每一个值的影响。

①思考。

师：如果你是评委，你会为夏齐羊打多少分呢？对平均分有什么影响？

②操作。

生：我想在10的基础之上降低2分。

师：刚才这位同学告诉老师，如果他是评委，他会将分数统一打低2分。你们猜平均数有什么影响？

③小结。

师：在这个过程中，你们有什么感受吗？

生：每一个值对平均数都有影响。一个值增加，平均数会增加；一个值减少，平均值会减少。

【设计意图：学生经历了“实物图——条形统计图”的抽象过程，依次在实物图、统计图中理解平均数。数形结合，让平均数可见。当然在这个环节中，对于平均数统计意义的理解还体现在以下三个方面：平均数是一个统计量、最小值＜平均数＜最大值、平均数受每一个值的影响。这三个层次意义的理解以问题情境串联，富有趣味性。在求平均身高时，感受到平均数的虚拟性；在分析平均分数时，感受到平均数的范围，发展学生思辨的能力；在现场打分过程中，通过改变数据感受到每一个值对平均数都有影响。】

三、练习提升，内化平均数

1.已知平均数找数。

（1）现在告诉你五个数的平均数是6，其中三个数都是6，那么另两个是多少？

（2）如果五个数的平均数是6，你能说一说这五个数分别是多少吗？

2.平均数的应用。

（1）独立思考。

已知小河平均水深140厘米，身高160厘米的尼克下水游泳。你认为他有危险吗？

（2）全班交流。

生：我觉得他不会有危险，平均水深140厘米，他的身高有160厘米，比平均水深高。可以安全过河。

生：我觉得会有危险。如果小河水深高低不一样，它只是平均水深是140厘米，那160厘米的尼克在水深深处会有危险。

师：看来！平均数是表示一组数的整体水平，不是代表每一个数都是这个平均数。

3.生活中的平均数。

师：同学们！想一想在生活中哪里会用到平均数？它表示什么？

【设计意图：本环节共有三个练习。练习1已知平均数找数，发展学生的逆向思维。练习2讨论“有危险吗？”培养学生画图以及思辨的能力，原来平均数是表示一组数的整体水平，不是代表每一个数都是这个平均数。练习3重在学生应用意识的培养。】

四、总结提升

师：通过这次疯狂奥运城之行，同学们有哪些收获？

【教学反思】

本课教学遵循“以学生为主体，教师为主导”的教学理念。

首先，创设了一个大情境激发学生学习的兴趣。接着出示情境一，思考“你觉得朱迪和尼克谁投得更准一些？你是怎么想的？”学生首先想到的是利用总数来比较，但是马上又会意识到次数也不一样。这时，急切需要创造一个能够考虑每一个值的数——平均数。一方面它的优点不言而喻，另一方面平均数的产生自然。在认知冲突中，引出平均数。

之后，学生进一步理解平均数的意义。对于平均数意义的建构需从意义开始，教学设计学生通过计算、移多补少得出了平均数。在移多补少的过程中，先后有实物图的移多补少、有示意图的移多补少，进一步抽象出统计图中的移多补少。形式的多样都是帮助学生理解移多补少的本质。

经历了平均数的产生，理解了平均数的意义，紧接着设计了三个环节，引导学生思考统计的意义，而这样的思考都是建立在一定有效活动之中的。在活动中，学生充分调动移多补少的经验先估再画找平均数的位置，进一步感知平均数的统计意义，平均数处于最大数与最小数之间。另外“形”的呈现给予学生对数的想象，一方面学生将“形”具体化，另一方面学生将“数”形象化，使得整个过程加深学生对于平均数的统计意义的理解。整个环节不是为了感受平均数的统计意义而感受，而是在任务的有效驱动下实现数学对平均数统计意义的建构。

数学来源于生活，应用于生活。在应用环节，教师不但考虑到学生应用于生活的能力，而且关注到对平均数统计意义的应用。两个练习各有突出，练习中学生充分根据生活经验、学习经验（平均数的统计意义）进行判断。在分析、比较的过程中，学生自然而然地内化平均数的统计意义。整个教学过程不仅培养了学生的数据分析能力，又提升了学生的创造能力。