高压压气机末级转子叶片振动特性分析
2020-07-08卞祥德
张 露,卞祥德
(1. 中国科学院工程热物理研究所 先进燃气轮机实验室 ,北京 100190; 2. 中国科学院大学,北京 1000493; 3. 中国科学院先进能源动力重点实验室(工程热物理研究所),北京 100190)
1 概述
压气机转子叶片振动分析是叶片结构强度(也叫结构完整性)[1]设计的一个重要组成部分。叶片振动问题造成的故障在我国发动机的研制、电厂燃气轮机的运行和天然气压气站压缩机组的运行等方面非常普遍。以航空发动机为例,振动故障率占发动机总故障率的60%以上,而叶片故障又占振动故障的70%以上[2]。叶片振动产生的故障导致的危害非常严重。若产生断裂掉块可能会打伤其它叶片,击穿机匣,造成二次损伤,甚至切开油路导致起火,发生严重事故。
压气机转子叶片的振动特性可以通过理论计算和试验两方面进行分析。张锦等对叶轮机叶片振动的解析计算法和有限单元法进行了详细论述和举例说明[3]。文献[4-10]均对压气机叶片振动特性进行了有限元计算和分析。王婧[10]通过激光全息照相的方法测量了叶片的固有振动特性,并与计算结果进行了对比。文献[11]针对压气机叶片的某个故障进行了模态分析,并通过坎贝尔图判断出导致叶片出现裂纹断裂失效的阶次。文献[12-13]分别采用不同方法对压气机转子叶片进行了模态分析。
某高压压气机第16级转子叶片(即末级叶片)曾多次发生相似的掉角断裂事故,现挑选出一个典型故障进行分析。2009年5月9日,西气东输定远站1#机组运行4 106小时后,孔探发现压气机第16级转子叶片76片全部出现了不同程度的损伤,如图1所示。
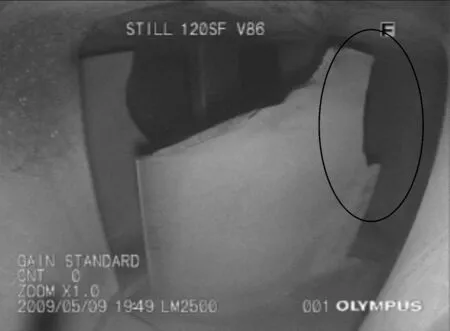
图1 故障叶片(圆圈内为初始断裂位置)
事发之后,为了排除故障采取了局部削角的措施。为对比分析故障叶片和削角处理的叶片的振动特性并为机器安全运行提供数值参考,本文针对该事例中的故障叶片(以下简称A叶片)和削角后叶片(以下简称B叶片)进行分析,主要开展了三个方面的工作:1) 叶片固有振动特性计算,绘制坎贝尔图;2) 叶片振动特性试验;3) 针对A、B两种叶片施加相同大小的简谐激振力进行频率响应分析。
2 研究方法
2.1 振动特性计算
利用UG建立叶片的三维模型(为简化计算模型,有限元建模时去掉了榫头和台肩四周的倒角),A叶片模型如图2(a)所示,叶展为28.5 mm。 B叶片叶尖和台肩削角位置如图2(b)和图2(c)所示。借鉴以前压气机叶片削角调频[2]的经验,B叶片进行相似的叶尖和台肩部分的削角处理,如图2(b)和图2(c)所示。将叶片三维模型导入ANSA划分网格,叶身和榫头等关键部位采用带有中间节点的六面体单元划分网格,转接段采用四面体单元,如图2(d)所示。A叶片单元数为13.4万,B叶片单元数为14.6万。根据叶片与轮盘的装配情况,限制榫头上表面的径向、轴向位移和榫头端部的周向位移,如图2(e)所示。

(a) 叶片模型
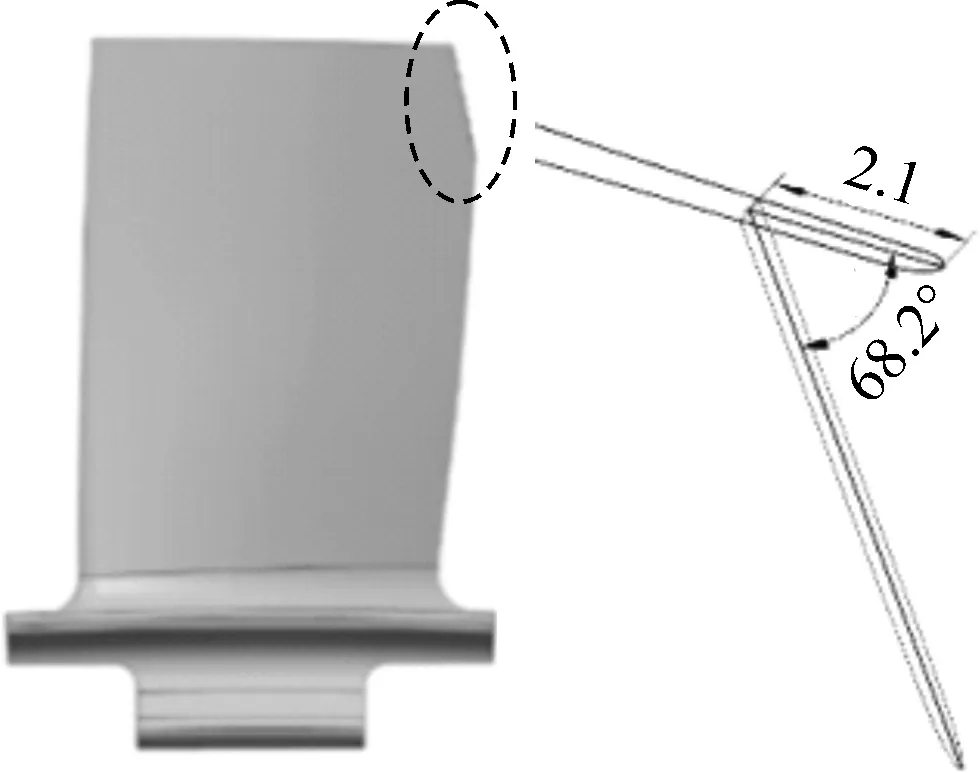
(b) 叶尖削角(单位:mm)
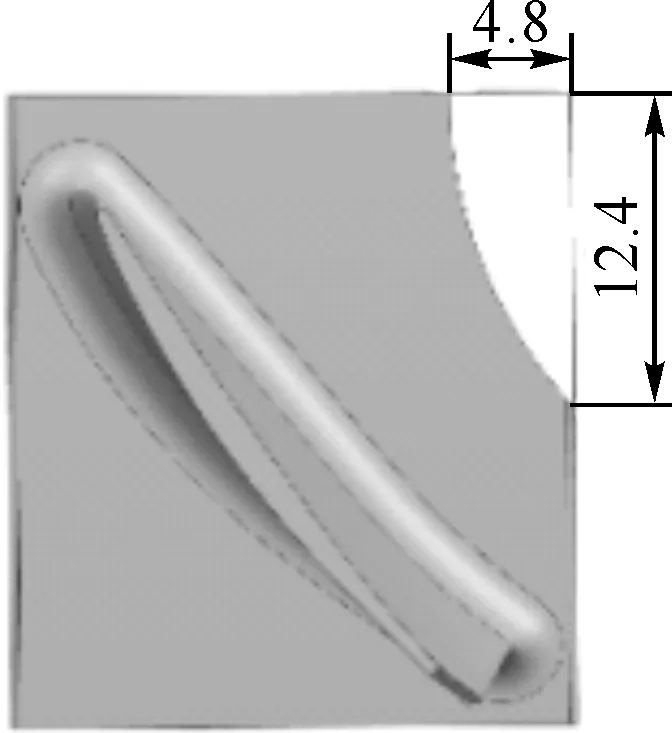
(c) 台肩削角(单位:mm)

(d) 网格模型

(e) 边界条件图2 叶片三维模型、网格模型和约束位置
该转叶材料选用GH4169。GH4169是镍基高温合金,密度为8.24 g/cm3,其它相关材料参数从材料手册[14]中查得。
叶片动频通过进行有预应力(离心力)的模态分析得到,离心力通过转速施加,分别设置转速为2 400 r/min,4 800 r/min,7 200 r/min,9 600 r/min,12 000 r/min,13 200 r/min进行计算。根据前期流体计算结果,工作转速下叶身温差比较小,由此热应力可以忽略不计。本文暂未考虑温度分布的影响,将叶身表面平均温度施加到叶片上。工作转速9 586 r/min,叶身平均温度为525 ℃;静止状态取叶身平均温度为20 ℃;中间转速叶身温度通过线性插值得到。叶片可能发生共振的危险振型通常通过坎贝尔图判断[15]。本文中考虑的激振力类型如表1所示。

表1 激振力类型
气体的尾流激振力用余弦载荷F0cos(ωt+φ)来表示[15]。为对比分析上游静子叶片排尾流激励对叶片削角后频率响应的影响,应用模态叠加法进行频率响应分析。根据流体计算结果,叶片沿径向的进口总压(周向平均值)在1.9 MPa到2.1 MPa之间,径向变化较小。现在对激振力做一定程度的简化,对A叶片和B叶片叶身前缘压力面相同矩形面积及位置处施加大小为1 MPa,垂直于径向且与周向夹角为45°的88倍频(14 059.47 Hz)激励,如图3所示。
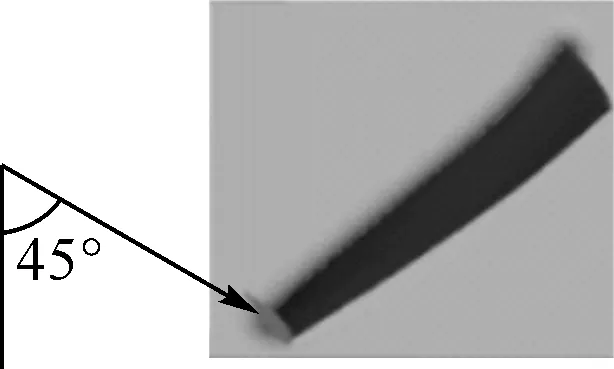
(a) 简谐激励作用方向

(b) 简谐激励作用位置图3 进口总压沿径向的分布及施加的简谐激励
2.3 振动特性试验
本次试验采用激光测振系统,如图4(a)所示,利用激光全息照相的方法测取A叶片和B叶片的固有频率。信号发生器将一定的电信号传递给压电晶体,使得压电晶体产生激励,激励作用在叶片上,使叶片产生强迫振动。激光发射器照射在叶片叶身上,CCD摄像机记录叶片振动的振幅和相位。
摄像机将得到的影像传递给数据采集装置,并在计算机上显示相应图像。当激励的频率接近叶片的固有频率时,叶片将会发生共振,此时计算机上显示的影像的明暗斑点逐渐收敛,明亮的斑点对应振动时保持不动的位置,即振动的节线,黑暗的区域对应振动时发生位移的位置。这时缓慢调节激励的频率,捕捉最清晰的图像。本次试验中,A叶片和B叶片各选取5片进行测试,以保证结果的可靠性。试验中叶片叶盆面朝向激光器(如图4(b)表示),压电晶体的黏贴位置如图4(c)所示。

(a)电子散斑振动测量系统

(b) CCD摄像机照射平面

(c) 压电晶体粘贴位置图4 电子散斑振动测量系统、CCD摄像机照射平面和 压电晶体粘贴位置
3 结果与讨论
3.1 振动特性计算和试验结果的对比
3.1.1 A叶片计算与试验结果的比较
从图5中A叶片叶身振型来看,A叶片第一阶模态为一阶弯曲振动,第二阶模态为一阶扭转振动,第四阶模态为二阶弯曲振动,第六阶模态为二弯一扭振动,第七阶模态为双扭弯曲复合振动,第八阶模态为弯扭复合振动。从计算与试验结果的比较可以看出计算出来的振型与试验得到的振型基本相符。由于计算出来的第三阶模态节线位置靠近叶根和台肩部位,第五阶模态节线位于台肩上,不易观测,这里未能观测到。从表2可以看出对于相同振型计算出来的频率与试验得到的频率(测得的叶片频率的平均值)差值f1-f2与试验值的比值在-4.66%~5.36%之间。计算设置的边界条件是理想状态。试验时为了固定榫头,用螺栓将榫头底部顶紧。两种约束方式不完全一样,且都与实际装配情况稍有差别,导致计算结果和试验结果稍有差别,但总体来看差值比较小,在误差允许范围内。

Mode 1

Mode 2

Mode 4

Mode 6

Mode 7

Mode 8

Mode 3


Mode 5(a) 仿真结果

Mode 1

Mode 2

Mode 4

Mode 6

Mode 7

Mode 8(b) 试验结果图5 A叶片叶身计算振型和测量振型
表2 A叶片计算频率和试验频率的对比

叶片模态计算值f1/Hz测量值f2/Hz(f1-f2)/f2Mode 12 3962 513-4.66%Mode 25 3655 297+1.28%Mode 39 024——Mode 410 0149 846+1.71%Mode 512 548——Mode 613 06212 552+4.06%Mode 714 95614 567+2.67%Mode 819 20618 625+3.12%Mode 921 25620 174+5.36%Mode 1023 534——
3.1.2 B叶片计算与试验结果的比较
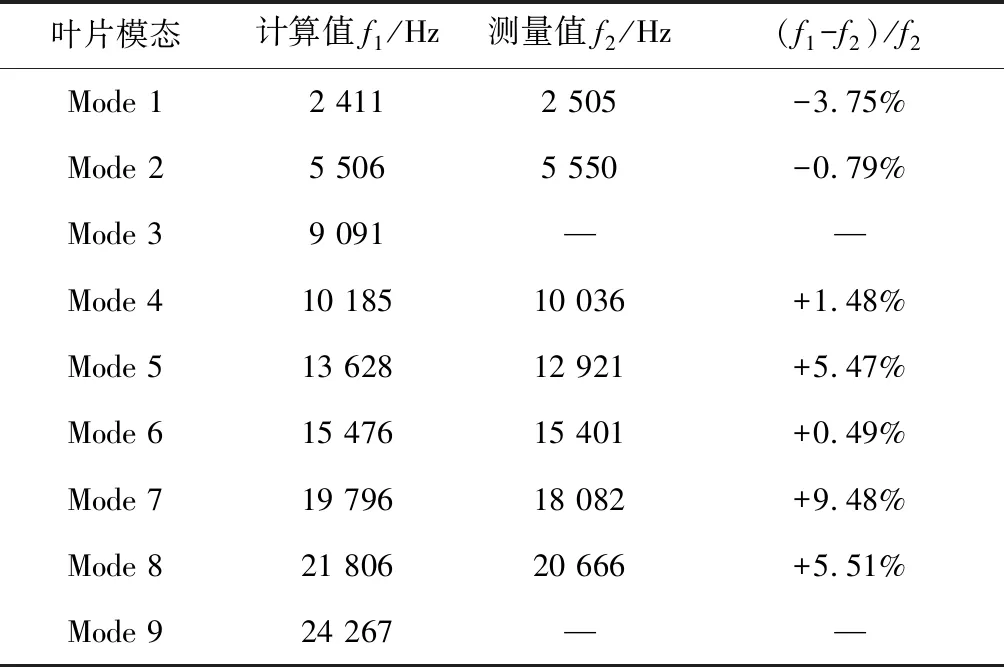
从图6中B叶片前八阶振型来看,B叶片第一阶模态为一阶弯曲振动,第二阶模态为一阶扭转振动,第四阶模态为二阶弯曲振动,第五阶模态为二弯一扭振动,第六阶模态为双扭弯曲复合振动,第七阶模态为弯扭复合振动。从计算与试验结果的比较可以看出计算出来的振型与试验得到的振型基本相符。由于计算出来的第三阶振型节线位置靠近叶根和台肩部位,不易观测,这里未能测量到。从表3可以看出对于相同振型计算出来的频率与试验得到的频率(测得的叶片频率的平均值)差值f1-f2与试验值的比值在-3.75%~9.48%之间。B叶片计算和试验采取的约束方式与A叶片相同,导致计算和试验结果稍有差别,但都在误差允许的范围内。

Mode 1

Mode 2

Mode 4

Mode 5

Mode 6

Mode 7

Mode 3(a) 仿真结果

Mode 1

Mode 2

Mode 4

Mode 5

Mode 6

Mode 7(b) 试验结果图6 B叶片叶身计算振型和测量振型
表3 B叶片计算频率和试验频率的对比
叶片模态计算值f1/Hz测量值f2/Hz(f1-f2)/f2Mode 12 4112 505-3.75%Mode 25 5065 550-0.79%Mode 39 091——Mode 410 18510 036+1.48%Mode 513 62812 921+5.47%Mode 615 47615 401+0.49%Mode 719 79618 082+9.48%Mode 821 80620 666+5.51%Mode 924 267——
3.3 坎贝尔图对比
相同振型下,B叶片频率比A叶片稍高,说明局部的微小几何变化对各阶振型的影响不大;B叶片频率比A叶片上升了0.5%~4.5%,这是由于削角之后叶片的径向刚度和弦向刚度略有增大,叶片频率升高。A叶片和B叶片前四阶模态中第二阶模态均为扭转振动,其余都是弯曲振动,对比频率可以发现,B叶片较A叶片扭转振动频率升高为2.62%,而弯曲振动频率升高分别为0.63%、0.74%、1.71%,说明削角对扭转振动频率的影响要略大于弯曲振动频率的影响。从图7中也可以看出,A叶片第五阶模态(如图5(a)所示)为台肩部分的振动,如果发生共振台肩部位很容易出现裂纹。B叶片没有相似的模态,从而从根本上去除了台肩部分发生裂纹的危险。
图7为A叶片和B叶片的坎贝尔图,从图中可以看出,随着转速的升高,叶片的各阶频率呈现下降的趋势。若不考虑温度的影响,在离心力的作用下,随着转速的提高,叶片刚性增加,叶片的弹性回复力增加,叶片频率较静止状态下要高;若考虑温度的影响,由于转速越高,流道内流体温度越高,从而导致叶片弹性模量降低,叶片频率下降。从图7中可以看出弹性模量对叶片频率的影响要大于离心力对叶片频率的影响,从而使叶片频率呈现下降的趋势。

(注:实线代表A叶片频率,虚线代表B叶片频率。)图7 A叶片和B叶片坎贝尔图对比
如图7中圆圈所示,工作转速附近,A叶片第7阶频率和B叶片第6阶频率在88倍频线上下10%的裕度范围内都有交点,A叶片和B叶片工作转速下均存在共振的危险。由图5和图6可知,A叶片的第7阶振型和B叶片的第6阶振型都是双扭复合振型,如果发生共振,叶尖很可能会出现裂纹。因此,下文主要针对88倍频激励进行频率响应分析。
3.4 频率响应对比
由图8 (a)可以看出A叶片最大位移响应位于叶片排气边靠近叶顶的位置,为0.044 mm;由图8(b)可以看出B叶片最大位移响应位于叶片排气边与削角的平面相交的位置。比较图8(a)和图8(b)可以看出,B叶片的位移响应为0.054 mm,比A叶片稍大,增大约23%。由图8 (c)可以看出A叶片最大Von-Mises应力响应为82.408 MPa,位于叶顶附近靠近排气边的位置;由图8(d)可以看出B叶片最大Von-Mises应力响应为78.848 MPa,位于叶片中上部靠近排气边的位置。比较图8(c)和图8(d)可以看出B叶片的最大Von-Mises应力响应比A叶片稍小,减小约4%,位置更靠近叶身,且Von-Mises

(a) A叶片位移响应云图

(b) B叶片位移响应云图

(c) A叶片应力响应云图

(d) B叶片应力响应云图图8 叶片位移和应力响应云图
应力较大的区域增大。与A叶片相比,B叶片共振点的振幅较大,但是Von-Mises较小。说明削角能够在一定程度上降低叶片共振时最大应力点的应力。
图9为88倍频激励(即14 059.47 Hz)上下10%范围内的频率响应云图,图中虚线表示88倍频激励。从图9中可以看出,削角后叶片的共振点最大振幅增大,但是最大Von-Mises应力却略有减小,说明削角在一定程度上降低了共振时叶片的等效应力。
4 结论
本文进行了A、B种叶片的静频和动频计算,并进行了振动特性试验,验证了计算的正确性。通过相同激励下的频率响应计算,对比分析了叶片削角前后的振动响应变化,可以得到以下一些结论:
(1) 在工作转速附近A叶片和B叶片与88倍频线的交点均未避开10%的裕度范围,极易因上游静子叶片排的尾流激励引发双扭复合共振。
(2) 通过88倍频激励下的响应可以看出B叶片位移响应更大,但是Von-Mises应力响应更小, 说明削角能够降低叶片振动时的应力。

(a) 位移(振幅)响应 (b) Von-Mises应力响应图9 叶片频率响应(12 000 Hz~16 000 Hz)
(3) A叶片第五阶振型主要振动部位在台肩位置,如果发生共振很容易导致叶片台肩部分出现裂纹。B叶片没有该振型,从而去除了台肩部分发生裂纹的危险。
