Joint inversion of magnetotelluric and fullwaveform seismic data based on alternating cross-gradient structural constraints

QI Jiahui, FENG Xuan, Enhedelihai Nilot and LI Xiaodan

College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China

Abstract: Magnetotelluric (MT) inversion and seismic inversion are important methods for the interpretation of subsurface exploration data, but separate inversion of MT and seismic produces ambiguous and non-unique results due to various factors. In order to achieve accurate results, the authors propose a joint inversion method of two-dimensional MT and seismic data in the frequency domain. The finite element method is used for numerical simulation of electromagnetic data in the forward modelling, and the Gauss-Newton method is used for the inversion. The 9-point-finite-difference method is used to solve the seismic wave field in the acoustic wave equation, and the inverse problem of seismic data is solved by full waveform inversion with a conjugate gradient, a simple and fast method. Cross gradient functions are used to provide constraint structure between resistivity and velocity parameters to carry out the joint inversion. The joint inversion algorithm is tested by double-rectangular model synthesis data, and the accuracy of the algorithm is verified. The results show that the joint inversion results are better than those from separate inversion. The algorithm is applied to a geophysical model of a metalliferous deposit in Jinchuan and is compared with the separate inversion results. It shows that the results obtained with joint inversion are much closer to the real model.

Keywords: alternating joint inversion; structural constraint; MT inversion; FWI

0 Introduction

Seismic and magnetotelluric (MT) exploration are very important methods of probing subsurface geo-logy. However, due to several factors, separate me-thods can not accurately illuminate underground structure (Huetal., 2006), therefore, it is necessary combining different geophysical methods and data types to reduce the uncertainties and errors.

MT exploration is a method for studying the electrical structure of the earth through naturally alternating electromagnetic fields (Cagniard, 1953). It is an extremely popular geophysical prospecting method, with the advantages of low cost, wide spectrum range, and a wide range of detecting depths (dozens of meters to several thousands of kilometers). It is not shielded by high resistance, and is sensitive to low resistance. However, as the exploration depth increases, the resolution gradually decreases.

Seismic exploration is a method for studying subsurface structure by observing and analyzing the changes in the propagation of artificially excited or natural elastic waves as the density and elasticity of subsurface media change. This method has a high resolution but is not very effective in areas with small velocity variation or poor stratification.

Joint inversion combines data from a variety of geophysical methods through a specific relationship to jointly invert a geophysical model of the subsurface, and achieves a unified interpretation of the target, increasing the reliability of the results (Jupp & Vozoff, 1975). A common joint inversion method is based on petrophysics, which establishes the relationship between different physical properties of underground media (Heinckeetal., 2006; Colombo & Stefano, 2007; Jegenetal., 2009). However, the relationship between different physical parameters varies with regions, many of these relationships are not well established and are inaccurate, so this method has limitations and inaccuracies. Therefore, some joint inversion methods based on structural consistency have been developed, of which, the most common one is the joint inversion method based on the cross-gradient function proposed by Gallado and Meju (2003,2004).

The joint inversion of MT and seismic data has been studied since the end of the 20th century, based on both petrophysical and structural constraint methods. Heincke (2006), Colombo (2007), and Jegenetal. (2009) accomplished the joint inversion of MT, seismic and gravimetric data by applying petrophysical methods, achieving better results than those achieved by separate method. Gallardo and Meju (2003, 2004, 2007) proposed the cross-gradient function to carry out the structural constraints, and achieved joint inversion of seismic and MT data and joint inversion of seismic and direct current resistivity data based on the structural constraints. Subsequently, Moorkampetal. (2011) applied the petrophysical method and the structural constraint method to the joint inversion. The results showed that the petrophysical method produces better inversion results when the relationship between various physical parameters is accurate, but when the relationship between the structural constraint physical parameters is not accurate, it produces false anomalies. However, the structural constraint method produces accurate results. In recent years, there have been many joint inversion studies based on cross-gradient structural constraints. Pengetal. (2013) achieved the three-dimensional joint inversion of seismic travel time and MT data. Benningtonetal. (2015) developed the joint inversion of natural earthquake and MT data based on the normalized cross-gradient constraint. Gao and Zhang (2016) studied the joint inversion of seismic travel time and full channel electrical measurements. Zhang (2017) accomplished joint inversion of gravimetric, magnetic, electric and seismic data, and carried out joint inversion research on the Liudaogou area of Linjiang City. Fengetal. (2017, 2018) undertook joint inversion of ground-penetrating radar and shallow seismic reflection data, and the joint inversion of seismic and audio magnetotelluric data. All the above studies indicate that joint inversion results are more accurate than separate inversion results.

In this paper, the joint inversion of seismic full-waveform inversion (FWI) and MT data in the two-dimensional frequency domain is studied. The finite element method is used in forward electromagnetic modelling, while the inversion uses the Gauss-Newton method. The 9-point finite difference method is used for seismic forward modeling, and a conjugate gradient method is used for seismic FWI to update the model. In order to simplify the calculation, the two inversion processes are carried out separately and alternately, and the structural constraints between them are realized by adding a cross gradient function. Then a simple double rectangle model is tested to verify the accuracy of the algorithm, and the Jinchuan metalli-ferous deposit model is tested to verify the practicability of the algorithm.

1 MT and seismic forward modeling and inversion

A key point of joint inversion is that each separate inversion has a fast and accurate forward modeling and inversion calculation.

1.1 Seismic forward modeling

The acoustic wave equation in an isotropic medium of constant density can be written in the frequency domain as follow:

(1)

By using the 9-point finite difference method to discretize equation (1) (Joetal., 1996; Pratt, 1990), the equations corresponding to the wave fields at each point in the calculated region can be written as the matrix equation:

B(m,ω)P(ω)=S(ω)

(2)

WhereBis a complex impedance matrix,mis the P-wave velocity vector,Pis the seismic wave field in the frequency domain, andSis the seismic source. The seismic wave field can be obtained by solving Eq.(2).

1.2 MT forward modeling

MT waves follow Maxwell’s equations. According to the direction of electromagnetic components, plane electromagnetic waves can be divided into TM and TE, with the wave equations:

(3)

(4)

WhereEyandHyare the electric and magnetic field intensity components, respectively,ωis the electromagnetic frequency,μ0is the permeability of a vacuum, andρis the resistivity. Under the boundary conditions,EyandHycan be calculated through the finite element method described by Rodi (1976), and the corresponding magnetic field(Hx)and electric field(Ex) can be calculated using the following equations:

(5)

(6)

Then the corresponding MT model response can be calculated using the following equations:

(7)

(8)

1.3 Seismic inversion

Seismic FWI is a method that makes full use of the dynamics and kinematics information in the pre-stack seismic wave field to estimate the elastic para-meters of the earth’s internal medium (Tarantola, 1984). This is carried out by finding a velocity model to minimize the difference between the observed data and the simulated data. In the frequency domain, only a few frequencies are selected for FWI. The final inversion results can be obtained by inverting the frequency from low to high. Comparing with the calculation in time domain, the formula is simple, and takes less time for large number of shots, but requires more memory (Vigh & Starr, 2008). The target function we defined is as follow:

(9)

WherePcalis the wave field corresponding to the current model,Pobsis the observed wave field,Wdis the diagonal weight associated with the offset distance,Tis the transpose, and * denotes the complex conjugate of the matrix.

The conjugate gradient method is used for the optimization. The basic idea of this method is to combine the conjugate property with the traditional steepest descent method and construct a group of conjugate directions using the gradient at the known points. The objective function searches along the group of directions and finally obtains the minimum value points of the objective function (Yao, 2002; Baeetal., 2012). The conjugate gradient method is widely used in optimization algorithms because it does not need to construct a large Hessian matrix, has a small memory requirement and converges quickly. Therefore, FWI in the frequency domain requires a large amount of memory, so the conjugate gradient method is adopted in this paper. The iterative formula is as follows:

mk+1=mk+αkΔmk

(10)

Wherekis the number of iterations,αkis the search step size based on the parabola method, andΔmkis the search direction. The calculation formula is as follows:

Δmk=-G(mk)+βkΔmk-1

(11)

WhereΔmkandΔmk-1is the conjugate andGis the gradient, which is the first derivative of the objective function to the model parameters.βkis a scalar quantity; calculated by the PRP method, the formula is as follows:

(12)

To calculate the gradient directly, a long process of solving the equation is required, which requires a large amount of calculation. Therefore, this paper adopts the adjoint state method to calculate the gradient. The physical meaning of this method is to take the data residuals as the conjugate inverse propagation of the forward operator, and then take the gradient of the target functional to the model (Tarantola, 1984). From Eqs. (11) and (12), we can see that we just need to calculate and record,G(mk),G(mk-1), andΔmk-1. Then, the disturbance model can be calcula-ted, and the computational complexity and the memory requirements are greatly reduced.

1.4 MT inversion

The MT inversion adopts the Gauss-Newton method. In this paper, to improve the stability of the solution of the inversion, Tikhonov regularization is added:

φMT(m)=(d-F(m))TCd(d-F(m))+τ(m-m0)TLTL(m-m0)

(13)

WhereF(m) is the forward function to calculate the response of the model,dis the response vector of the observed model,mis the resistivity vector,τis a Lagrange regularization parameter,Cdis the data covariance matrix,m0is the initial model resistivity vector, andLis a second-order difference operator. Our purpose is to find the optimal solutionm, so as to minimize the value of the objective function. When updating the resistivity model, the Gauss-Newton method not only uses the first derivative of the objective function, the gradient (G), to model parameters, but also uses the second derivative of the objective function, the Hessian matrix (H), so the speed of convergence is fast, but the number of calculations is very large (Prattetal., 1998). In order to reduce computation, we calculate the gradient and the Hessian matrix by calculating the Jacobian matrix:

G=JTCd(d-F(m))-τLTL(m-m0)

(14)

H=(JTCdJ+τLTL)-1

(15)

WhereJ=∂F(m)/∂mis the Jacobian matrix, calculated by the reciprocity theorem. In order to prevent the morbidity of the Hessian matrix, we introduce the Marquardt attenuation factor (ε), and the model update quantity changes to

Δm=(H+εI)-1G

(16)

The model update equation is now:

mk+1=mk+Δm

(17)

2 Joint inversion

In order to improve the accuracy and stability of MT and seismic inversion, joint inversion of MT and seismic data is adopted in this paper, and the cross-gradient function proposed by Gallardo and Meju (2003) is used to impose structural constraints on the resistivity and velocity models. The cross-gradient expression is

φcross(x,y,z)=ms(x,y,z)×mr(x,y,z)

(18)

φcross=ms(x,z)×mr(x,z)

(19)

Fig.1 shows the calculation of the cross gradient of two different two-dimensional models.

As it can be seen from the Fig.1:

(a)Model 1; (b) model 2; (c) cross gradient for model 1 and model 2.Fig.1 Cross-gradient for two models

(1) When the spatial variation directions of the physical parameters of the two models are the same or opposite, the cross-gradient is equal to 0.

(2) When the spatial variation directions of one models’ physical parameters change while the other remains unchanged, the cross-gradient also equals 0.

(3) When the spatial variation directions of the two models’ physical parameters are neither the same nor opposite, the cross-gradient does not equal 0. The greater the difference is, the higher the cross-gradient value will be.

Therefore, the physical significance of the cross-gradient is that when there is a common boundary between the two models, the cross-gradient acts as a constraint on the inversion results of the two models.

Considering inversions of different geophysical datasets, the discretization of the models and data is different, and the sensitivity to the model is different, so the corresponding data inversion system fully coupled into a large joint inversion system for calculation with cross gradient structure constraints is very complicated. Therefore, the two inversion processes are separately and alternately carried out, and the cross-gradient function is directly added to each individual inversion objective’s function, thus realizing the structure coupling of the resistivity and velocity models. The idea of the inversion is to select the same number of frequencies, and invert the MT and seismic data alternately frequency by frequency. In this way, when updating the resistivity model at each iteration, not only the data fitting and model constraints, but also the velocity model constraints obtained from the previous frequency are considered. Similarly, when the velocity model is updated, it is constrained by the resistivity model obtained for the previous frequency. In this way, a connection is established between the two models through the cross-gradient function. The whole inversion process is divided into an inner loop and outer loop, the outer loop is a cycle of frequencies, and the inner loop is an inversion calculation at one frequency. When the inversion at a particular frequency completes and the process starts with a new frequency, the final model of the old frequency is used as the initial model under the new frequency, until the set maximum frequency is reached, the whole inversion is cut off, and the final model is produced. This is repeated until both inversions have reached the set precision requirements or the maximum number of iterations has been reached. Therefore, the objective function of the joint inversion algorithm consists of the following two parts:

φMT(mr,ms)=(d-F(mr))TCd(d-F(mr))+τ(mr-mr0)TLTL(mr,mr0)+αφcross(mr,ms)

(20)

(21)

Whereαandγare the weighting factors, representing the proportion of the cross-gradient function in the target function. Thus the gradient in the resistivity model update becomes:

GMT=G1+αmrφcross

(22)

The Hessian matrix becomes:

HMT=H1+α2mrφcross

(23)

And the gradient in the velocity model update becomes:

GS=G2+γmsφcross

(24)

WhereG1,G2andH1are the separate MT and seismic inversion gradients and Hessian matrix, respectively.mφcrossis the first derivative of the cross-gradient term in the model parameters, andmmφcrossis the second derivative of the cross-gradient term in the model parameters. In this paper, the cross-gradient function is discretized using the central difference method. The first derivative of the cross-gradient function to the resistivity parameter is discretized as follows:

(25)

Fig.2 Joint inversion flowchart

The second derivative of the cross-gradient function for the resistivity parameters and the first derivative for the velocity parameters can be obtained by a similar method.

The joint inversion process is shown in Fig.2.

3 Model trial

First, the joint inversion algorithm is used to test a simple model, and the joint inversion results and the separate inversion results are also compared. The real model is shown in Figs.3a，b. This model includes a high-velocity and high-resistance rectangular anomalous body and a low-velocity and low-resistance rectangular anomalous body. The size of both abnormal bodies is 0.5 km×0.5 km, and the top depth is 0.2 km. The velocity of the high-velocity and high-resistivity anomalous body is 4 000 m/s, and the resistivity is 1 000 Ω·m the velocity of the low-velocity and low-resistivity anomalous body is 2 000 m/s, and the resistivity is 10 Ω·m. The background is a uniform half space with a size 1.0 km×2.5 km, velocity of 3 000 m/s, and resistivity of 100 Ω·m. The mesh is with an equal spacing of 50 m. 25 seismic sources are placed 100 m underground, with a spacing of 100 m between the sources. There are 50 receivers on the ground and 20 receivers on each side of the boundary, with spacing of 50 m. The MT field has 50 receivers equally spaced on the surface.

(a) True electrical resistivity model; (b) true seismic velocity model; (c) resistivity model from separate inversion; (d) velocity model from separate inversion; (e) resistivity model from joint inversion; (f) velocity model from joint inversion.Fig.3 Comparison between separate inversion and joint inversion of simple model

The seismic source uses the Ricker wavelet with a main frequency of 30 Hz, and the FWI takes eight inversion frequencies ranging from 1 Hz to 8 Hz. The MT inversion takes 8 frequencies from 1 Hz to 1 000 Hz, and the frequency increases exponentially. The initial model is a uniform half space, with velocity of 3 050 m/s and resistivity of 100 Ω·m.

Fig.3 shows the resistivity and velocity models obtained by separate and joint inversion of MT and seismic data, respectively. It can be seen that, for the resistivity model, the center position and resistivity values of the anomalous bodies are well depicted by separate inversion, but the boundaries are not well defined, particularly for the high-resistivity abnormal body. For the joint inversion, the boundary of the anomalous body is better depicted, and the shape of the anomalous body is consistent with the real model. For the velocity model, the position, boundary and velocity of the anomalous body are well characterized by separate FWI. Compared with separate inversion, joint inversion does not show much improvement, with some small perturbations eliminated.

(a) Profile at depth of 0.35 km; (b) at depth of 0.55 km; (c) profile in distance of 0.75 km; (d) in distance of 1.65 km.Fig.4 Comparison of MT inversion results with different depths and distances

In order to compare the inversion results more precisely, taking the resistivity at depths of 0.35 km and 0.55 km, and horizontal distances of 0.75 km and 1.65 km of the true model, as shown in Fig.4 to compare the resistivity obtained from separate inversion and joint inversion. It shows that the results obtained by joint inversion are closer to the real model in numerical value, and the contour characterization is improved.

Similarly, we compare the P-wave velocity profiles at the same locations, as shown in Fig.5. Since the precision of separate FWI is quite high, joint inversion does not offer much improvement. Only in a few places is the velocity value closer to the real mo-del and the curve smoother.

In order to compare the results of joint inversion and separate inversion quantitatively, the model errors are calculated using the following formulaes:

(26)

(27)

In order to test the effect of the joint inversion, inversion of the model of Jinchuan metallic deposit is undertaken. The geological structure and physical parameters of the metallic deposit are illustrated in Fig.7.

The mesh of the model used in the inversion is 50×40, with an equal spacing of 50 m. 25 seismic sources were placed 100 m underground, with a spacing of 100 m. There are 50 receivers on the ground and 40 receivers on each side of the boundary, with spacing of 50 m. The MT field has 50 receivers equally spaced on the surface. The seismic source uses the Ricker wavelet with a main frequency of 30 Hz, and the FWI takes eight inversion frequencies ranging from 1.5 Hz to 8.5 Hz. The MT inversion takes 8 frequencies from 1 Hz to 1 000 Hz, and the frequency increases exponentially. The initial model is a uniform half space with velocity of 2 400 m/s and resistivity of 300 m.

It can be seen from Fig.8, the results of the joint inversion of MT are obviously superior to the separate inversion results. The separate inversion only shows the center of the anomalous bodies and their general shape, and the trend of the deep anomalous body deviates from the actual model. Moreover, there is a clear high-resistance false anomaly at the lower right of the anomalous body. The boundary of the abnormal body is better depicted by joint inversion, the morphology of the abnormal body is closer to the actual model, and the false anomaly at the lower right of the abnormal body is suppressed.

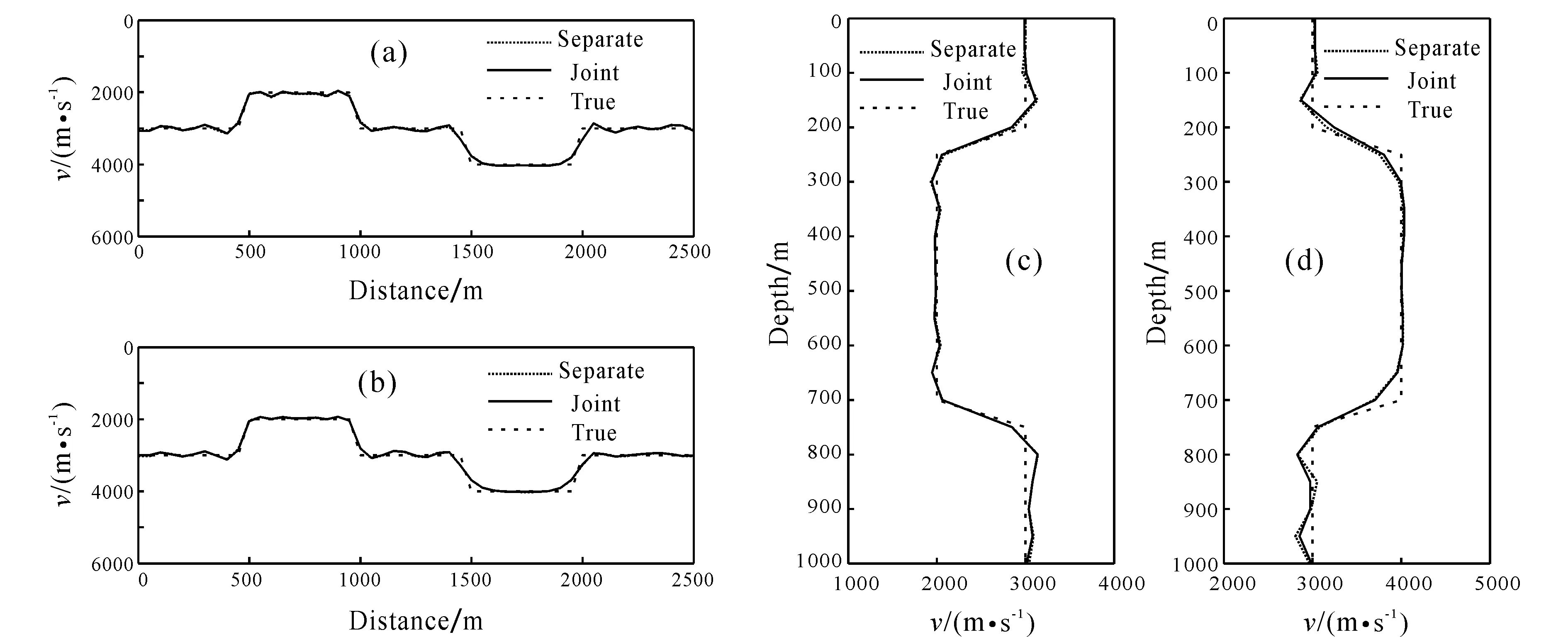
(a) Profile at depth of 0.35 km; (b) at depth of 0.55 km; (c) profile in distance of 0.75 km; (d) in distance of 1.65 km.Fig.5 Comparison of seismic inversion results at different depths and distances

(a) Resistivity model; (b) velocity model.Fig.6 Comparison of double-rectangular model errors

Fig.7 Geophysical profile of Jinchuan metallic deposit

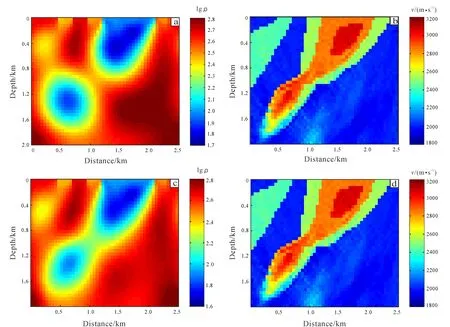
(a) Resistivity model from separate inversion; (b) velocity model from separate inversion; (c) resistivity model from joint inversion; (d) veloci-ty model from joint inversion.Fig.8 Comparison between separate inversion and joint inversion of metallic deposit model

The results of separate seismic inversion are quite good. The morphology and numerical characteristics of the subsurface structure are very close to the actual model, and there is only a small disturbance near the deep abnormal body. The results of joint inversion are not better than those of separate inversion.

(a) Resistivity model; (b) velocity model.Fig.9 Comparison of Jinchuan metallic model errors

Fig.9 is the model error calculated by Eqs. (26) and (27). The cross-gradient term is added in the objective function from the third frequency in the magnetotelluric joint inversion, while the cross-gradient term is added in the objective function from the second frequency in seismic joint inversion. As can be seen from the error curve in Fig.9, after using the joint inversion, the error between the obtained resistivity model and the real resistivity model is reduced from 0.54% to 0.39%, and the velocity model only has a small decline in error. Compared with the separate inversion, the joint inversion has a modest improvement.

4 Discussions and conclusions

The purpose of joint inversion is to use a variety of geophysical properties to invert subsurface targets simultaneously. Different geophysical methods make use of different physical properties, and different geophysical methods have different resolution and applicability to underground targets. Therefore, using multiple geophysical methods can reduce the non-uniqueness of the inversion solution and improve the accuracy.

MT inversion and seismic inversion are very effective geophysical methods for subsurface studies. MT methods have a wide range of detection depths and are not shielded by high resistance, but have low resolution. Seismic inversion has a high resolution, but is not good for inversion of regions with poor stratification. In this paper, the joint inversion of seismic FWI and MT data in the frequency domain is accomplished by the structural constraints based on cross-gradient coupling proposed by Gallado and Meju. In the joint inversion, because the orders of magnitude of different physical properties may be different, if they are directly combined into an objective function, the overall calculation of the model update amount will raise computational difficulties. In this paper, the objective function is divided into two parts, and the two inversions calculate the corresponding model update, with the constraints between the two inversions established by cross-gradient terms. Finally, the algorithm is applied on a simple model with two rectangular anomalous bodies, and data synthesized by the Jinchuan metallic deposit model. The results show that joint inversion is better than separate inversion, particularly for the MT inversion, the structure of the anomalous body from joint inversion is closer to the real model.

In addition, considering the FWI calculation in the frequency domain is very computationally expensive. In this paper, the conjugate gradient method is used to calculate updates to a velocity model. This method uses a set of conjugate directions as the search direction of the objective function, which only needs to calculate the gradient, and does not need to calculate the Hessian matrix, and greatly reduces the computational load and storage space requirements.