一种波束域主模式抑制算法
2020-07-07楼万翔
楼万翔,黄 迪
(中国船舶重工第715研究所,浙江杭州310023)
0 引 言
为了提高探测能力和增加探测距离,现代声基阵孔径越来越大,阵元个数越来越多,造成自适应算法的运算量和计算复杂度成倍数增加,这严重阻碍了自适应算法在声呐信号处理中的应用。在有限的资源下,减少自适应算法的运算量且同时保证算法的性能是目前解决这一问题的一种途径。
主模式抑制(Dominant Mode Rejection, DMR)方法[1-4]利用特征分解来构造一个主模式子空间,通过对该空间内矢量进行抑制达到在低信噪比情况下检测弱目标的目的。该方法不需要对自相关矩阵进行估计、求逆等运算,具有计算量小、收敛速度快等优点,因而在近期得到广泛研究。常规的DMR算法往往是在阵元空间中进行的,当阵元个数成倍数增加时,阵列的自相关矩阵维数也相应成倍数增加,急剧加大了特征分解的计算量,运算速度也相应降低。同时在实际处理中,由于角度偏差和阵元间距误差等因素导致自相关矩阵失配,从而影响该算法的稳健性。
为了解决这一问题,本文把算法从阵元空间转换到波束空间中。波束空间的自适应算法有波束域MVDR (Beam MVDR, BMVDR)[5-6]、波束域ESPRIT(Beam ESPRIT, BESPRIT)[7]、波束域求根Music(Beam Root-Music, BRoot-Music)[8]。根据前人的研究成果,本文提出了一种波束空间DMR(Beam Dominant Mode Rejection, BDMR)。BDMR算法通过波束转换矩阵把阵元域空间转换到波束域空间,实现了降维处理,在保证算法性能的同时,减小了运算量,提高了算法的稳健性。通过仿真实验,BDMR算法与DMR算法性能相近,但是其运算速度和稳健性均得到了提高。
1 阵元域DMR算法
假设存在一个满足半波长布阵的N阵元的均匀线列阵。实际信号的入射角为θs,信噪比为rSNR。实际存在的干扰数目为D,干噪比为rINR,入射角度为:θ1、θ2、⋅、θD。主波束指向为θ,方向矢量为Vm。设阵列自相关矩阵的估计值为Rx。对Rx做特征分解得到

式中:λi为特征值,Φi为其所对应的特征向量。根据特征值的大小可以将其分成两部分:Dm个较大的特征值,其所对应的特征向量构成信号子空间,也即主模式子空间;N-Dm个较小的特征值,其所对应特征向量构成噪声子空间,即次模式子空间。Rx改写为
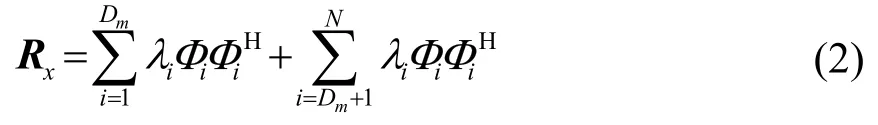
计算可得最后N-Dm个小特征值的平均值为

在具有1个入射信号和Dm-1个干扰信号的环境下,该平均值代表了估计得到的白噪声的功率。
对自相关矩阵进行修正,修正结果为
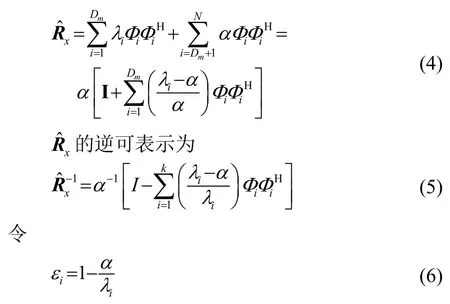
式中,εi称为抑制系数,0<εi<1。主模式抑制算法求解权重向量的过程与MVDR相同,但是用代替Rx,约束形式为
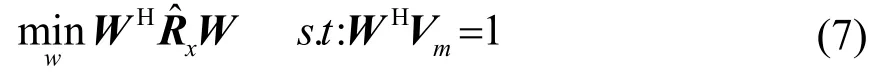
DMR算法的自适应权值W的最优解形式为

把式(5)和式(6)代入式(8),计算得到DMR算法的自适应权值W为
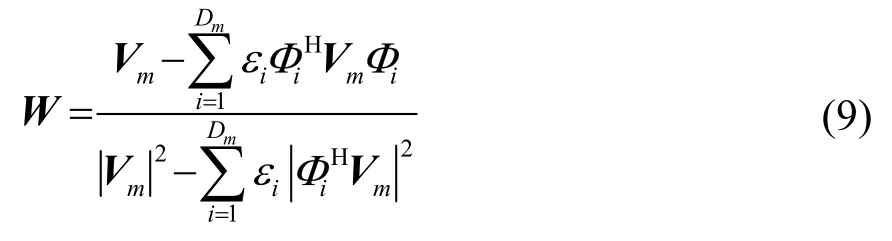
2 BDMR算法
在实际应用中当阵元个数增加时,阵元域DMR算法的运算量相应增加,同时算法的稳健性降低。然而通过合理的选择波束形成预处理矩阵,将阵元域空间的DMR算法转化到波束域空间中,可以降低矩阵维数、减少运算量并且提高算法稳健性。
假设阵元域输出数据为Xk,在所观测的空间中利用l个连续的波束输出估计目标方位,则得到的波束域输出数据Yk可表示为

式(10)满足线性转换。式中T是波束转化矩阵,其表达式为
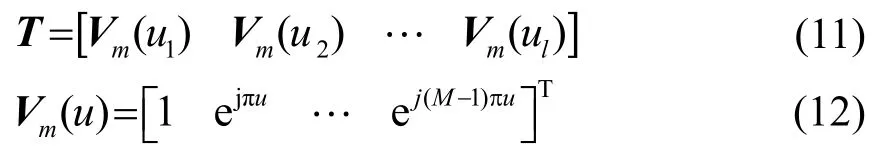
其中,l是形成的波束数,M为阵元域数据Xk中的阵元个数,u表示形成波束的主瓣方向。
利用转化矩阵T中的几列,即目标方位附近的NBS个波束,由该NBS个波束对应的阵列向量组成的矩阵定义为TB,则
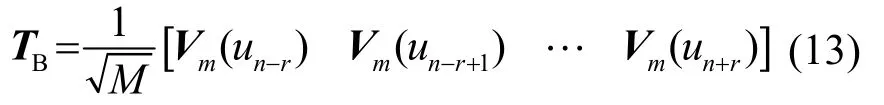
式中:n是与目标估计方位最接近的波束号。由转化矩阵T的性质可知,TB也是正交的。由此可得波束域自相关矩阵RB和波束域方向矢量分别为

对RB进行特征分解,可得:

根据第1节阵元域的DMR算法,可得BDMR算法的自适应权值计算为
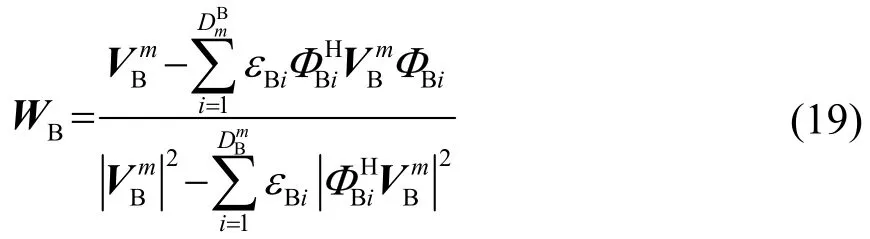
BDMR把阵元域空间转换到波束域空间,自相关矩阵Rx从N×N维降到RB的NBS×NBS维,在大孔径声基阵中波束的个数一般要小于阵元的个数,因此在阵元数大于波束数的情况下,BDMR的计算复杂度要小于DMR。
3 仿真分析
现对BDMR性能进行仿真分析,仿真条件为32元均匀线列阵,阵元间距为1.2 m,处理频率范围为300~1 000 Hz。设有一目标方位角为10°,利用目标附近的9个波束进行波束域转换。常规波束形成器(Conventional Beamforming, CBF)、主模式抑制波束形成器(DMR)和波束域主模式抑制形成器(BDMR)的波束形成结果如图1所示。

图1 单目标的3种算法的波束形成结果Fig.1 The beamforming results of three algorithms for a single target
从图1中可知,CBF的主瓣宽度为3.00°(-3 dB处),旁瓣高度为-13.3 dB;DMR的主瓣宽度为0.35°,旁瓣高度-41.4 dB;BDMR的主瓣宽度为0.44°,旁瓣高度为-36.7 dB。
增加另一目标,其方位角为13°,信噪比与目标1一致,双目标的波束形成结果如图2所示。
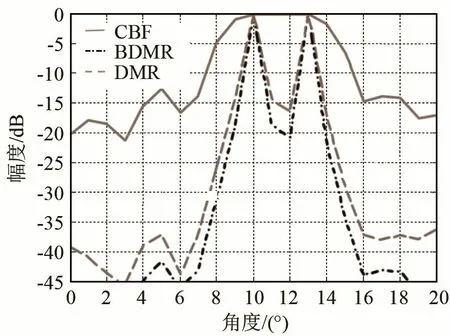
图2 双目标的3种算法的波束形成结果Fig.2 The beamforming results of three algorithms for two targets
从图2中可知,CBF算法已经不能分辨这两个目标;而DMR和BDMR算法都能清晰分辨出两个目标,DMR算法的目标峰值与两目标间的谷值相差-20.8 dB,BDMR算法该差值为 -16.5 dB。
从以上仿真结果可以看出,BDMR算法的波束宽度略大于DMR算法,但明显小于CBF;BDMR算法的旁瓣略高于DMR算法,但是明显小于CBF;DMR算法、BDMR算法的分辨性能都优于CBF,BDMR算法的分辨性能略差于DMR算法。综上所述,BDMR算法的性能明显优于CBF,但略差于DMR算法,但是基本保留了DMR算法的性能。阵元间距增加一个随机扰动,造成阵型失配,坐标如图3所示,阵型失配后的单目标和双目标3种算法的波束形成结果如图4、图5所示。
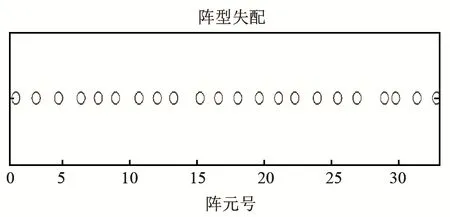
图3 阵元间隔失配后的阵型Fig.3 Array formation after elements spacing mismatching
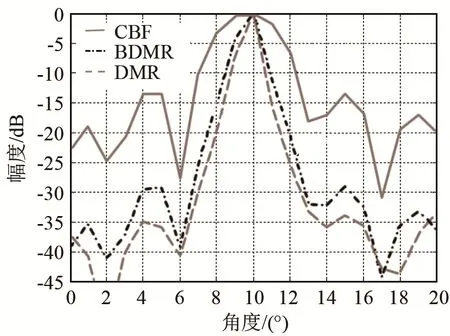
图4 阵元间隔失配后单目标的3种波束形成结果Fig.4 The beamforming results of three algorithms for a single target when element spacing mismatching
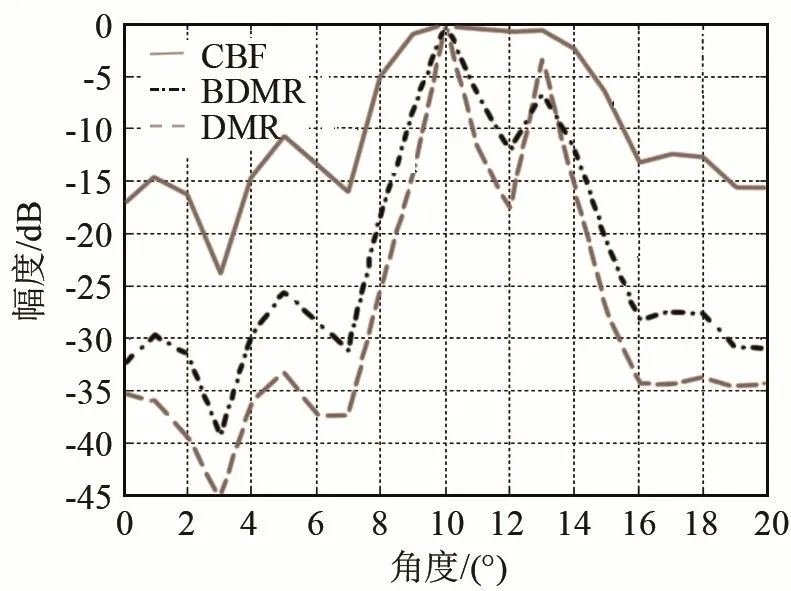
图5 阵元间隔失配后双目标波束形成结果Fig.5 The beamforming results of three algorithms for two targets when element spacing mismatching
从图4中可知,CBF的主瓣宽度为3.30°(-3 dB处),旁瓣高度为-13.4 dB;DMR的主瓣宽度为0.95°,旁瓣高度-29.1 dB;BDMR的主瓣宽度为0.70°,旁瓣高度为-33.9 dB。
从图5中可以看出,CBF不能分辨这两个目标;而DMR和BDMR都能清晰地分辨出两个目标,DMR算法目标峰值(主瓣位置较低的目标)与两目标间的谷值的差为-5.3 dB,BDMR算法该差值为-14.2 dB。
从仿真结果可以看出,当阵型失配时,BDMR和DMR的主瓣宽度变大,BDMR的波束宽度略小于DMR;3种算法的旁瓣都有不同程度的增高,但BDMR的旁瓣略低于DMR;阵型失配后BDMR和DMR的分辨性能都降低,但是BDMR要略优于DMR。综上可知,在阵型失配时,BDMR比DMR的稳健性更好。
利用Matalab软件比较DMR和BDMR的运算量,分别比较32个阵元和64个阵元的运算速度,结果如表1所示。当阵元数较少时,BDMR运算时间略多于DMR;当阵元数增加1倍时,DMR运算时间急剧增加,而BDMR运算时间只是略微增加。结果表明,当阵元数较多时,BDMR运算速度远远快于DMR。
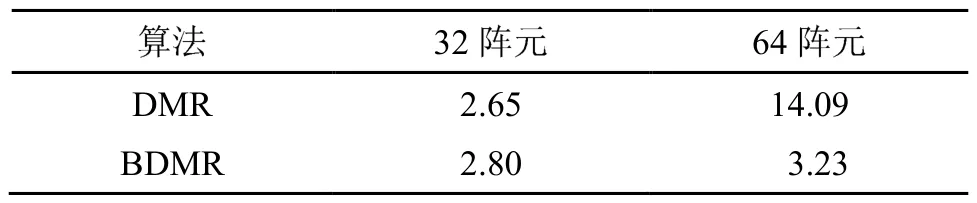
表1 两种算法的计算时间比较(s)Table 1 Comparison of computation time of two algorithms(s)
4 结 论
本文把DMR算法从阵元域空间转换到了波束域空间,提出了一种BDMR算法。BDMR算法保留了原算法性能,同时提高了运算速度,计算复杂度(operational complexity)从O(N3)降到,减少了因阵元数目增加带来的计算量。在阵型失配时,BDMR比DMR具有更好的稳健性。但是在实际应用中,BDMR需要一定的目标所在方位的先验知识,这可通过CBF进行粗测,同时转换到波束空间后,秩减少了的BDMR,意味着降低了自由度的数目,所以可以抑制的干扰数目就减少了。
