一种声速-位置联合估计的水声导航定位方法
2020-07-07李瑨瑶王海斌
李瑨瑶,王海斌,汪 俊,徐 鹏,陈 曦
(1.中国科学院声学研究所,北京100190;2.中国科学院大学,北京100190)
0 引 言
水下航行器是一种可以凭借自身的动力系统和导航系统来完成水下工作任务的集成系统[1],在军事应用和民用方面均有广泛的需求。军事方面的应用包括:水下探测[2]、水下巡航以及水下中继通信等[3];民用方面包括:海洋资源开发、海洋环境监测以及海洋救险与打捞等。无论军用还是民用需求,一般都需要已知水下航行器的位置状态,故获取水下航行器的高精度位置信息成为需要解决的关键问题。目前水下航行器导航技术主要包括:航位推算与惯性导航、地球物理属性导航、声学导航。
航位推算与惯性导航方法分别利用速度传感器及加速度传感器得到水下航行器的速度及加速度,并利用其速度或加速度进行时间积分,从而推算出水下航行器的位置。但这种方法极易受到水流速度的影响,造成结果不准确。地球物理属性导航利用水下磁场强度特征、重力场特征、地形环境图等数据进行匹配定位,但需进行大规模的复杂调研及测绘工作,故至今实际应用较少。声学导航利用声音信号在水下传播衰减较小、传播距离较远的特点,将水面或水下已知位置的信标作为参考位置,通过测量信标发射的脉冲信号到达水下航行器的时间,计算信标到水下航行器的距离,从而得到水下航行器的位置信息[4-7]。声学导航主要包括超短基线导航[8]、短基线导航[9]和长基线导航等方式[10-12]。水下航行器的声学导航定位误差主要由水下等效声速的测量误差产生[13-16]:当水下航行器与信标位置距离较远时,由于信道传输环境复杂,准确估计等效声速较为困难,产生一定的距离估计误差,影响估计精度。为解决这一问题,本文引入粒子滤波算法将等效声速作为待估计量进行状态跟踪。粒子滤波算法是一种基于序贯重要性采样的序贯蒙特卡洛方法,不受系统线性化误差和高斯假设的限制,常用于解决状态跟踪问题。经过改进的粒子滤波算法,通过随机产生大量粒子的方式对目标状态进行模拟,根据观测信息判断粒子的拟合程度并赋予粒子相应权值,可以更高效地在先验信息未知的情况下对目标进行状态跟踪。针对声学导航定位由于等效声速估计误差带来的定位误差较大的问题,本文提出了一种基于粒子滤波的水声导航定位方法,将等效声速作为未知的估计参量加入状态方程中,建立以水下航行器的位置及各信标到水下航行器的等效声速为核心估计参量的粒子滤波算法模型,对水下航行器的位置进行估计。对上述方法的性能进行了仿真分析,并与常规长基线导航定位方法进行了性能对比。
1 问题描述及解决思路
常规的长基线水声导航定位利用信标发送的脉冲信号到水下航行器的传播时间作为观测量信息,将估计或测量得到的等效声速作为已知的参数,将两者相乘计算出各个信标与水下航行器的距离,在已知信标位置的前提下,利用距离的几何关系,计算出水下航行器的位置信息,其框图如图1所示。但无论是工程实测还是理论计算,由于水声信道的复杂性,将得到的等效声速作为已知参量都存在误差。这一误差会导致水下航行器的定位误差随着导航距离的增加而变大,因此,如何高精度地获取等效声速成为提高水声导航定位精度的关键问题。
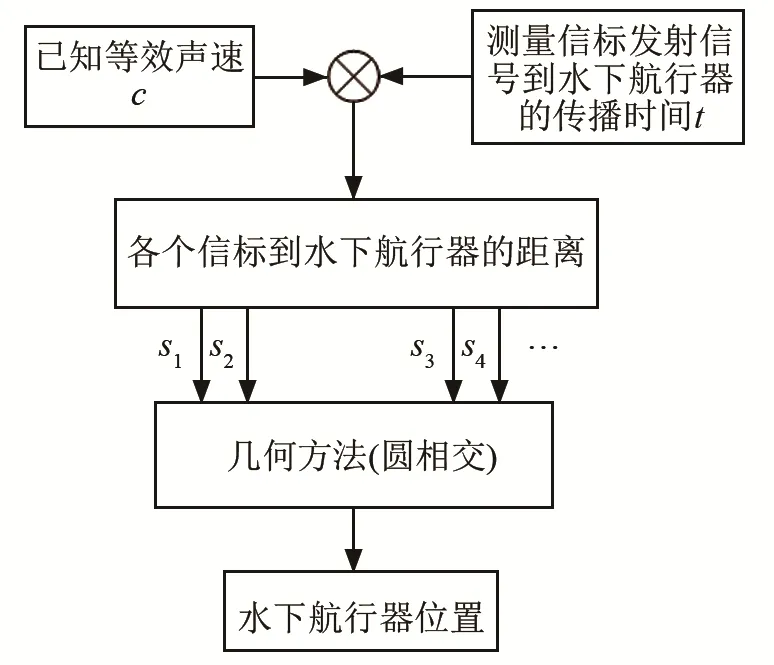
图1 传统水声导航定位方法框图Fig.1 Traditional underwater acoustic positioning method
针对这一问题,本文提出了一种基于粒子滤波的水声导航定位方法(如图2所示),将等效声速和水下航行器的位置作为未知的状态估计参量,结合观测期间航行器自身的速度分量,组成运动状态方程。将各个信标信号的传播时间作为测量值,后验概率密度函数会在较为准确的等效声速和水下航行器的位置处出现峰值。建立粒子滤波模型,利用估计得到的后验概率密度峰值获得水下航行器的位置及等效声速的最优解,从而得到每个时刻水下航行器的位置及等效声速的估计值。将粗估的等效声速值作为粒子滤波算法中等效声速估计的初始值,将等效声速作为未知状态参量,通过状态跟踪,不断修正等效声速的估计误差,从而获得更高精度的定位。
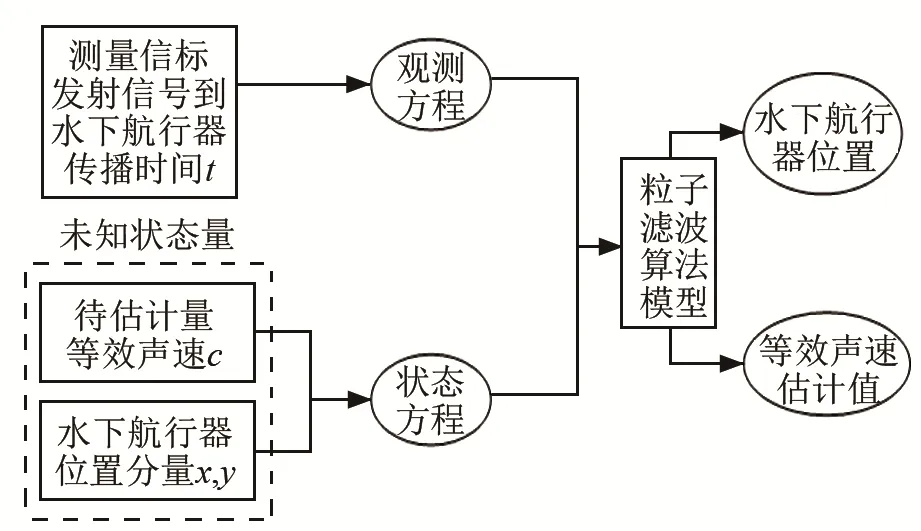
图2 本文所提基于粒子滤波的水声导航定位方法框图Fig.2 The method of underwater acoustic navigation and positioning based on particle filter proposed in this paper
2 基于粒子滤波水声导航定位方法
2.1 粒子滤波基本原理
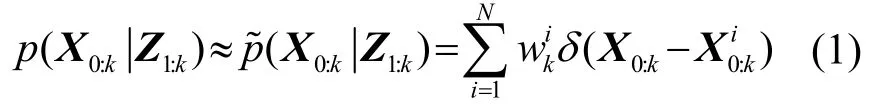
式中:δ为单位冲激函数,为k时刻每个粒子对应的权重,并且。但目标概率密度函数p(X)非常复杂,无法直接产生符合概率密度函数的粒子,因此利用重要性采样(Importance Sampling)方法,设是较之容易实现采样的概率分布密度函数,称为重要性函数,若重要性密度只取决于Xk-1和Zk,定义重要性权重wk为
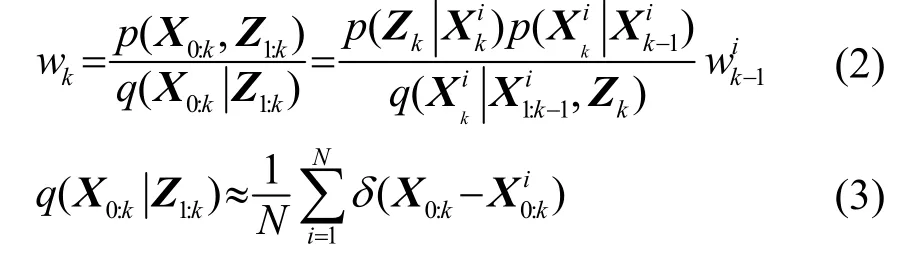
但粒子滤波存在退化问题,因此,需要利用重采样来解决粒子退化问题。重采样的步骤包括对的离散近似表达进行重采样N次后得到一个新的集合:
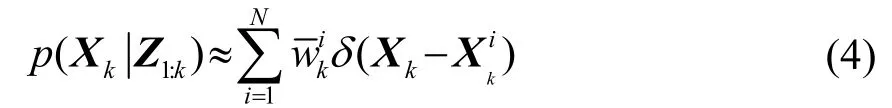
2.2 基于粒子滤波算法的水声导航定位模型
信标数目设置为m,在导航过程中每个信标的位置坐标不变,为(xos,yos)(s=1,⋅⋅⋅,m,下同),航行器在k时刻的位置为(xk,yk)。k时刻第s个信标到航行器的等效声速为csk,从第k时刻到k+1时刻、第s个信标到航行器的等效声速改变量为。k时刻第s个信标到航行器信号的传播时间为tsk,其测量误差分别为nsk,并假设nsk满足零均值高斯分布。通过航行器惯导系统得到k时刻航行器的速度(vxk,vyk)(即从k时刻到k+1时刻航行器位置的变化量),但由于速度测量存在误差,假设航行器速度测量误差服从零均值高斯分布。
k时刻待估计的状态参量为

首先随机产生M个粒子,每个粒子包含的预估状态参量,对每个粒子根据观测方程给出粒子对应的权值,采样-重要性重采样(Sampling-Importance Resampling,SIR)滤波器将重要性函数选择为先验函数,代入式(2)中可以得到重要性权值为

该滤波器每个时刻都进行重采样,因而:

重要性权值在重采样步骤前需要进行归一化,之后的每个时刻都进行重采样操作。因此粒子的权值可以表示为
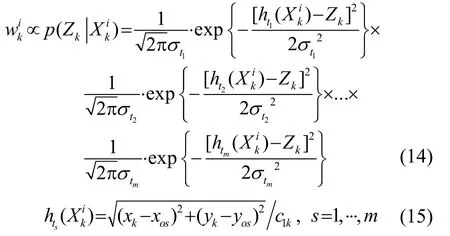
对每个粒子加权平均估计当前时刻目标的运动状态,并进行对当前时刻粒子重采样,得到重采样后的粒子。在下一时刻,将重采样后的粒子代入粒子的状态方程中:

式中,A为根据目标运动状态得到的逆推矩阵。由式(16)可得到下一时刻的粒子并重新为粒子分配新的权值,继而得到下一时刻估计得到的目标运动状态。
2.3 基于粒子滤波算法的水声导航定位方法
算法输入:每个信标的发射信号到航行器的传播时间;由航行器惯性导航得到的航行器每个时刻的运动速度。
(1) 在每个时刻随机产生大量粒子模拟的航行器位置以及各个信标信号传播到航行器的等效声速,对应得到这一时刻每个粒子的权值;
(2) 对每个时刻的粒子加权估计航行器位置及各个等效声速;
(3) 进行重采样处理重新得到粒子并代入状态方程中获取下一时刻的粒子;
(4) 循环此过程得到每个时刻状态估计值。
算法输出:每个时刻航行器位置分量、各个标信号传播到航行器的等效声速估计值。
基于粒子滤波的导航定位算法流程图如图3所示。
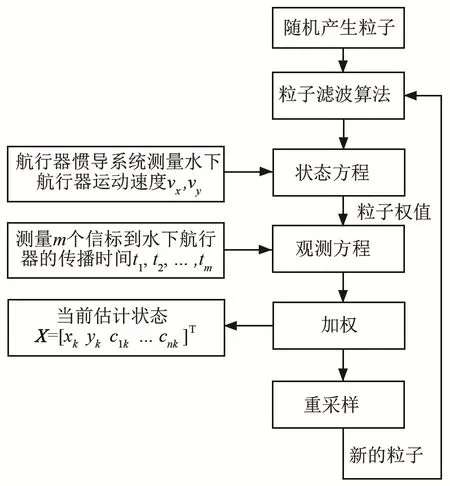
图3 基于粒子滤波的导航定位算法流程图Fig.3 Flow chart of navigation and positioning algorithm based on particle filter
3 仿真分析
取正北方向为0°,设置3个导航信标B1、B2和B3。三者构成一个边长r=60 km的等边三角形,B1位于坐标原点(0,0)处,B2位于坐标(r,0)处,B3位于坐标处。航行器初始位置位于S点,坐标为(3r/4,r/5),做匀速直线运动,速度为2.5 m·s-1,航向为75°。在实际应用中,航行器即使做匀速直线运动也会受到水流影响,假设水流速度在x和y方向都存在扰动,且其速度扰动均满足均值为0、标准差为0.71 m·s-1的高斯分布。k时刻与k+1时刻的时间间隔为120 s,时间采样次数为100次。假设3个信标的信号同时收到。信标信号传播时间的测量误差均服从均值为0、标准差为31.6 ms的高斯分布。3个信标到航行器的等效声速真值分别为c1=1 510 m·s-1、c2=1 519 m·s-1,c3=1 503 m·s-1(声速真值在后续处理中未知),且由于航行器位置逐渐变化,等效声速缓慢变化,假设其变化量服从均值为0、标准差为0.1 m·s-1的高斯分布,等效声速的变化是为了模拟实际应用中由于环境变化以及航行器运动导致的等效声速改变。粒子滤波算法假设航行器初始位置未知,设定为距离航行器真实位置较远的坐标(r,5r/2),设置等效声速初始估计值分别为c1=1 502 m·s-1、c2=1 521 m·s-1、c3=1 496 m·s-1,与常规几何算法的等效声速估计初始值大小相同,标准差均取40 m·s-1;利用粒子滤波算法估计航行器位置须给出与其真实位置误差较大的初始位置,将航行器位置的初始值设置为(r,r/4),x轴与y轴坐标的标准差均取20 000 m。其中,c1和c3两个等效声速初始估计值误差较大,在航行器位置完全未知以及等效声速误差较大的情况下进行水声导航定位。常规导航算法利用圆相交的几何关系,等效声速取初始估计值对航行器定位,并将粒子滤波算法与常规方法的定位结果及误差进行对比。
图4为水下航行器与3个信标每时刻的真实位置。图5分别为3个信标信号到水下航行器的等效声速真值。图6、7分别为水下航行器的真实速度及真实航向角。图8、9分别为常规方法和基于粒子滤波对航行器进行导航定位的轨迹估计及误差对比。图10为粒子滤波算法对各信标的等效声速估计与等效声速真值的对比。
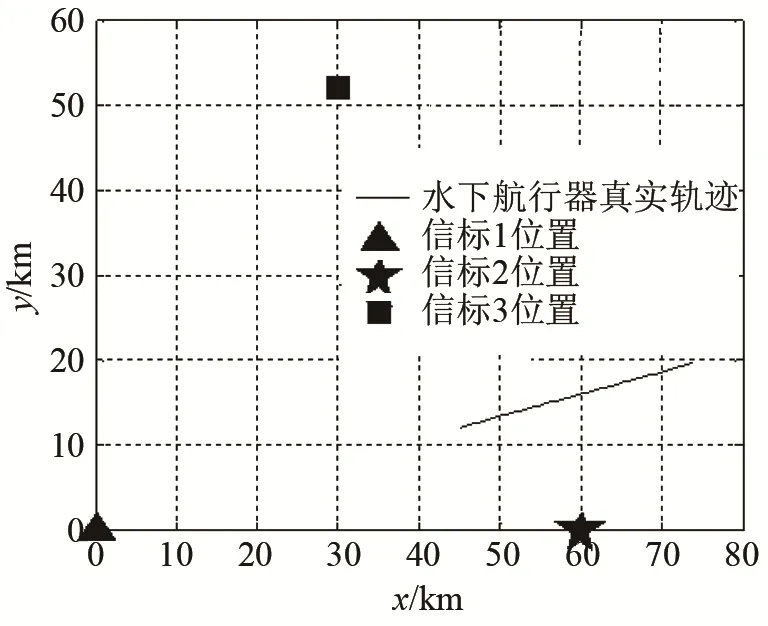
图4 水下航行器、信标位置及运动轨迹Fig.4 Position and trajectory of underwater vehicle and beacon
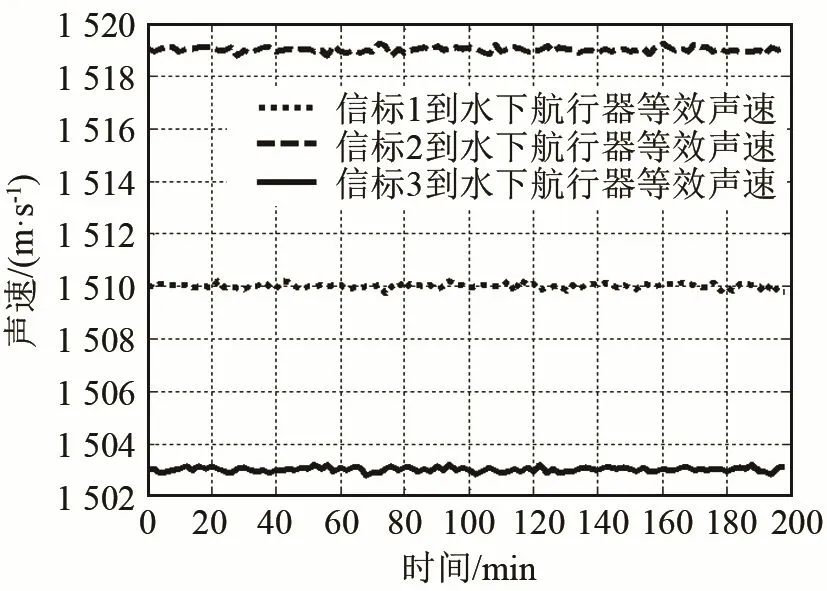
图5 各信标到水下航行器等效声速真值Fig.5 The true value of equivalent sound velocity from each beacon to the underwater vehicle
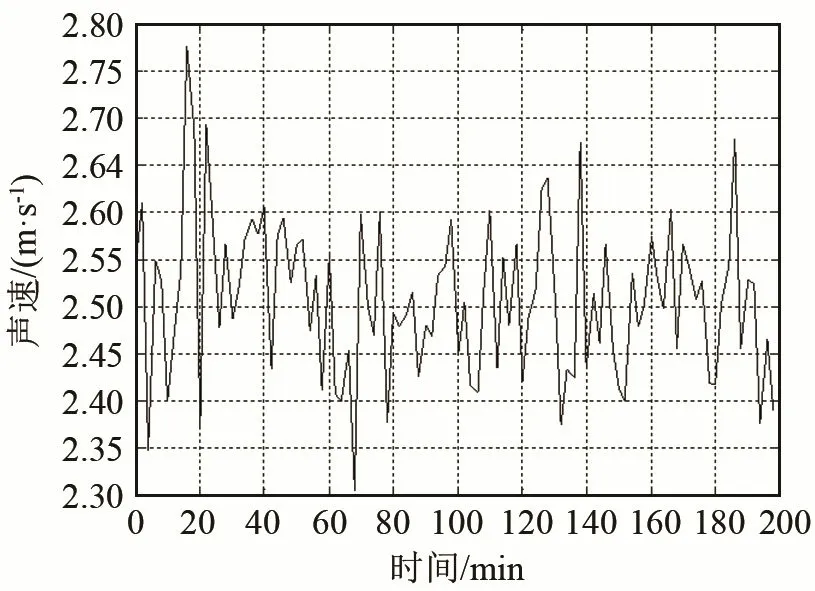
图6 水下航行器速度真值Fig.6 The true value of underwater vehicle speed
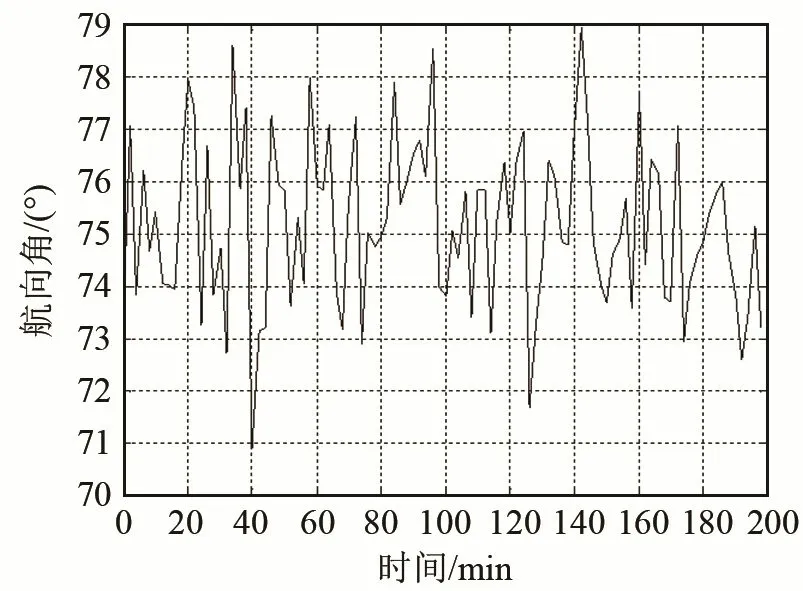
图7 水下航行器真实航向角Fig.7 The true value of underwater vehicle true heading angle
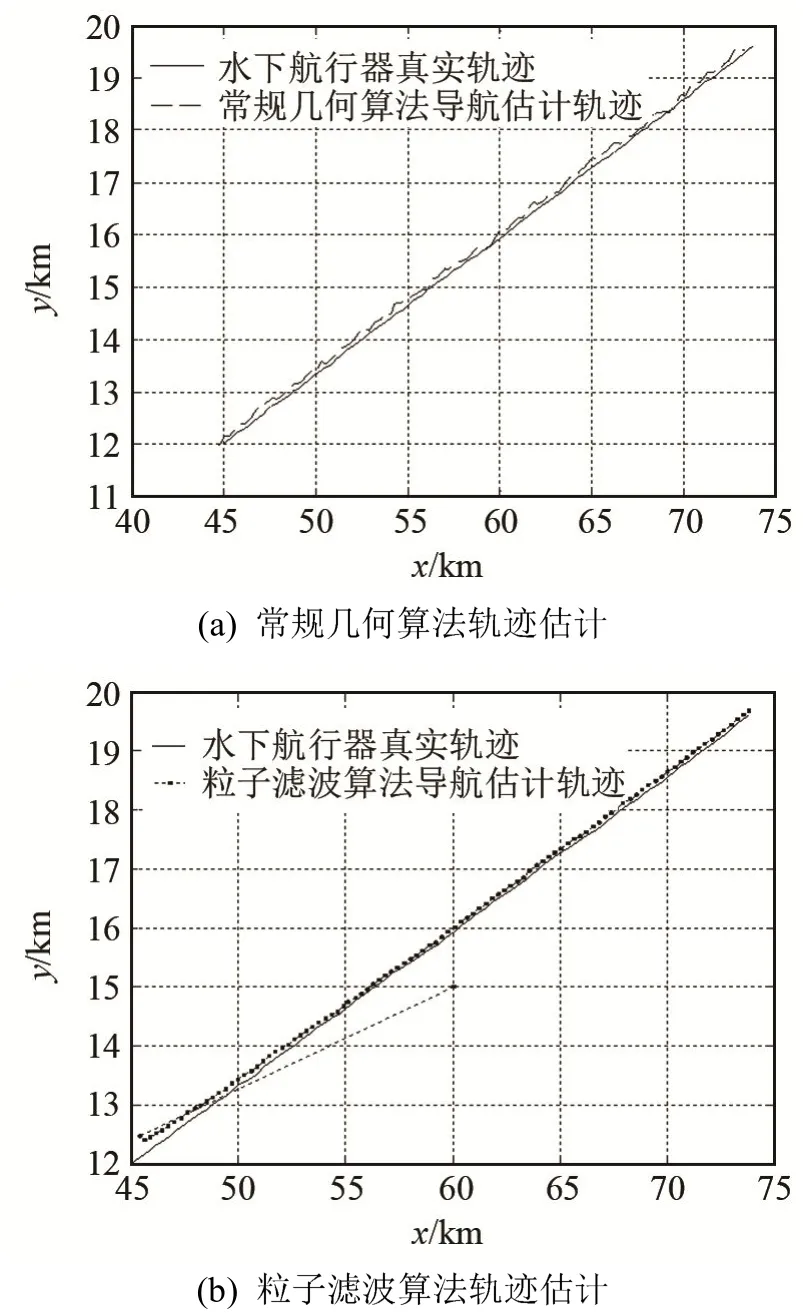
图8 常规算法及粒子滤波算法时水下航行器轨迹估计结果Fig.8 Trajectory estimation using conventional algorithm and particle filter algorithm
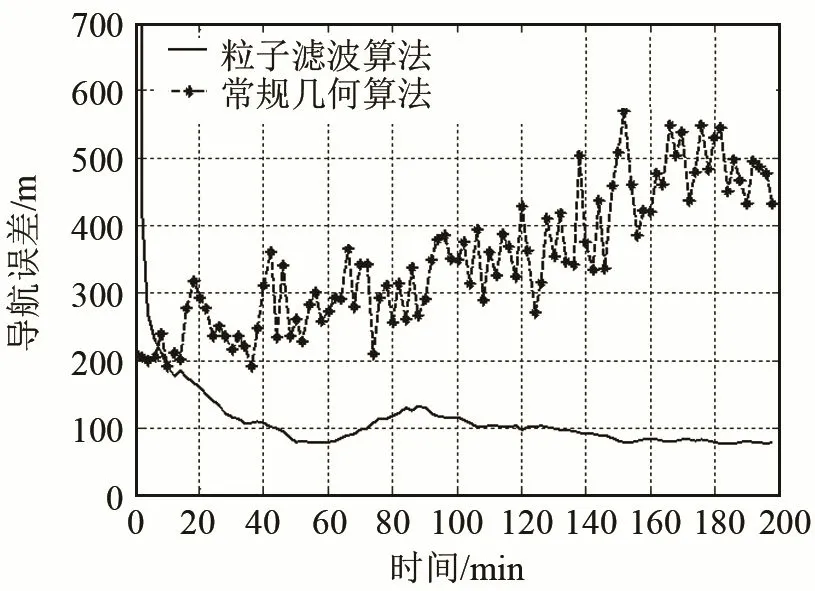
图9 常规算法及粒子滤波算法误差对比Fig.9 Error contrast of conventional algorithm and particle filter algorithm
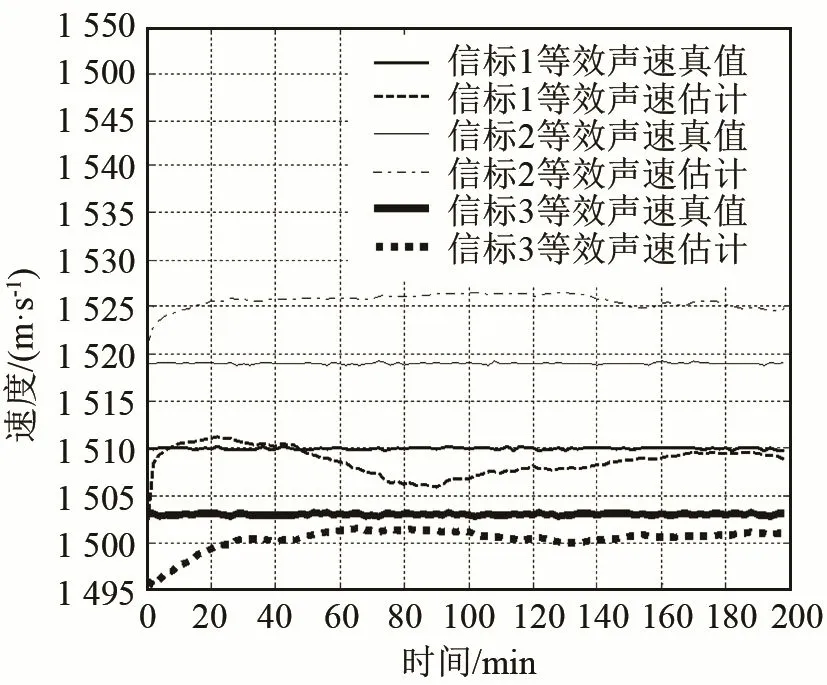
图10 粒子滤波算法对各信标的等效声速估计Fig.10 Estimation of equivalent sound velocity for each beacon using particle filter algorithm
由图8可得:粒子滤波算法估计的轨迹与真实轨迹更加吻合。由图9可知:常规方法在采样时间的末尾时刻误差大于初始值产生的误差,定位误差由200 m增加至400 m以上,而粒子滤波算法将定位误差控制在100 m左右,远小于初始定位误差,对水下航行器的定位更加准确。由图10可知:粒子滤波算法将等效声速作为未知状态量进行估计,在递推处理过程中估计值逐渐趋向真值,这是粒子滤波算法比常规方法定位更加准确的原因。
4 结 论
本文提出了一种基于粒子滤波算法的水声导航定位方法。该算法在每一时刻将大量不同状态的粒子代入信标信号到水下航行器的传播时间的非线性观测方程中,通过采样-重要性重采样滤波器分配每个粒子的权值比重,得到最优状态估计值。该方法基于粒子滤波模型,将等效声速和水下航行器位置作为未知估计状态,不仅减小了常规几何算法因等效声速误差产生的定位误差,而且随着时间推移,精度逐渐提高,在水下航行器位置完全未知的状况下能更准确地估计其运动状态,定位精度提高到原来的4倍左右,具备较高的应用价值。
