波数空间中活塞辐射体近场声压分布的计算及测试

卫相润，贺西平，崔晓娟，蒙永红

(陕西师范大学物理学与信息技术学院，陕西西安710119)

关键字：倏逝波；轴向声压；圆形活塞

0 引 言

大功率超声的应用日益广泛，如：超声焊接、超声悬浮、超声除泡、超声凝聚、超声清洗等[1-5]。在超声应用领域有很多应用活塞式辐射的实例。利用超声波进行测量、控制、探伤的过程中，圆形活塞式辐射体的应用非常广泛。因此，研究圆形活塞的振动声辐射特性具有普遍的意义。

文献[6]利用叠加法和高斯数值积分算法推导了多阶梯圆盘轴向声压的分布，计算了轴向声压随距离的变化关系，通过实验测试得到了轴向辐射声压与输入电功率、圆盘的阶梯数目之间的关系。文献[7]根据点声源辐射声场理论，利用点源合成方法推导得到了圆形活塞声源非均匀振动的辐射声场分布和指向性函数。

波动现象所引起的振动以及相应的辐射问题，可以用波数空间来描述。通常，这种描述方式对揭示表象下所蕴含的物理意义非常有效。角谱法的基本思想是将波分解成无数个平面波，通过平面波的叠加来计算声场的传播[8]。依据角谱法的基本思想，声场中某一点的声压可以唯一且完整地由平面波和倏逝波的叠加来表达。文献[9-10]中提出了近场声全息技术，近场声全息既可以记录传播波成分，又可以记录倏逝波成分。

本文以圆形活塞为例，利用角谱法求得活塞辐射声场的传播波和倏逝波的分布。利用数值分析方法[11]，对圆形活塞声源声轴线上的声压进行计算，得到相应的近场声压分布曲线。通过不同声源半径、不同辐射频率下的声压分布曲线的比较，得出了近场声压的变化规律。对所设计的阶梯圆盘的轴向声压进行了测试，实验测试结果与理论计算结果的趋势基本吻合。

1 传播波与倏逝波

超声速声波这一概念在1995年由Williams提出[12]。超声速声波是指声波在传播方向上的相速度比声速大[13]。波动方程的稳态平面波解由普通的平面波和倏逝波两部分构成。传播波的相速度比声速大，即为超声速声波，可以通过普通平面波的叠加而得到，对近场声压和远场声压都有贡献。倏逝波的相速度比声速小，即为亚声速声波，传播过程中倏逝波的幅值随距离按指数规律衰减，因而只对近场声压有贡献。所以在远场只能检测到传播波。

1.1 波数空间

波动现象所引起的振动以及相应的辐射问题，可以用k-空间来描述，这种描述方式对揭示表象下所蕴含的物理意义非常有效。如果我们构造矢量，其中，那么矢量k指向即为平面波的传播方向，任何平面波的传播方向都可以由矢量k=kxi+kyj+kzk确定。

因而平面波能够用如下的更为简洁的公式ei(kxx+kyy+kzz)=ei(k⋅r)来表示，其中，r=xi+yj+zk表示声场中观测点处的位置矢量，矢量k给出了波的传播方向。

1.2 传播波

无源的稳态声波亥姆霍兹(Helmholtz)方程为

其三维的通解为

满足：

利用逆傅里叶变换，并且不考虑时间依赖性，可得在频率ω0下的解为

其中：k为声波波数，k=2π/λ，λ为声波的波长，k=ω0/c，c为声速。

考察y=0时xz平面上的声压。令ky=0，，其相位φ为φ=kxx+kyy+kzz-ω0t。其中：x方向的相位为kxx-ω0t，波长λx=2π/kx，相速度cx=ω/kx；z方向的相位为kzz-ω0t，波长λz=2π/kz，相速度cz=ω/kz。

图1表示xy平面的波数圆，半径为k，可见传播波对应的波数分量末端端点落在波数圆内。

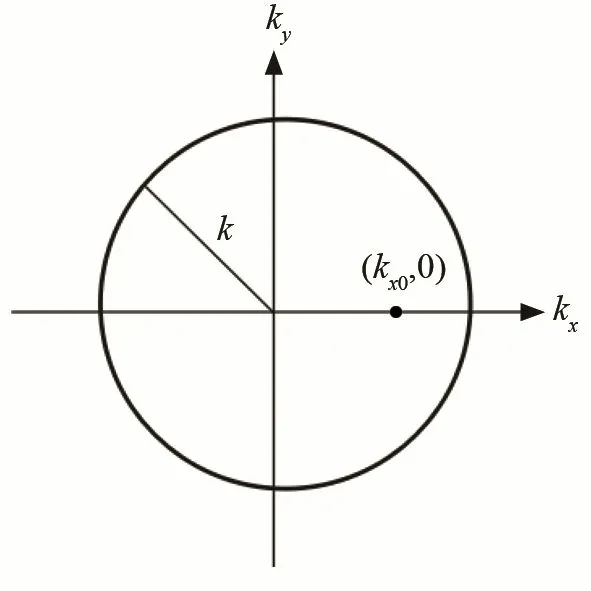
图1 平面传播波对应的波数圆Fig.1 Wavenumber circle corresponding to plane propagation wave

设θ为波的传播方向与z坐标轴的夹角，由于k=ω/c，kx=ksinθ，kz=kcosθ，则：cx=c/sinθ，cz=c/cosθ，可见，cx、cz均大于声速c，即为超声速声波。

1.3 倏逝波

在式(3)中，kx与ky为独立的自变量，它们与声源所在的平面结构有关，分别为波数沿x、y方向上的空间频率分量。而kz为因变量，其取值依赖于前两个自变量，它表示声场中的传播波成分或倏逝波成分。可以看出，波的传播性质和传播方向取决于kx、ky的大小。若，则对应的波即是倏逝波。

kz是虚数，，由式(2)可得：

式(5)可以表示倏逝波的声压，声压在z方向上的幅值呈指数衰减。同理可知，若cx＜c，即为亚声速波。图2表示xy平面的波数圆，半径为k，可见倏逝波对应的波数分量末端端点落在波数圆外。

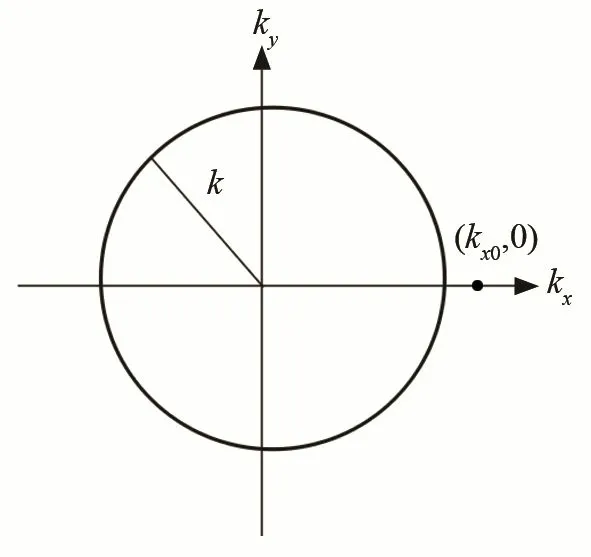
图2 倏逝波对应的波数圆Fig.2 Wavenumber circle corresponding to evanescent wave

2 角谱法

2.1 角 谱

考察在z＞0的自由半空间中，一个未知的稳态声压分布为p(x,y,z)。该声压能够唯一且完整地由具有上述形式的平面波和倏逝波的叠加来表达[14]。构成声压的平面波和倏逝波可能有不同的幅值和相位，通过乘以一个依赖于kx与ky两个波数的系数项p(kx,ky)，希望无源自由场中的任意声压分布都可以表达为一组波的叠加，如

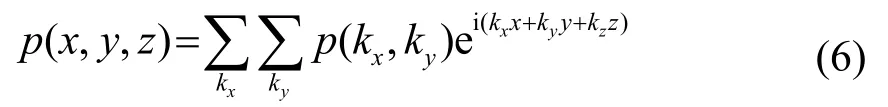
式中的指数项作为平面波或者倏逝波。由于x方向与y方向可以无限地延伸，希望波数有连续性，因而将式(6)的求和式化为连续积分。于是，声压场更具一般性的表达为

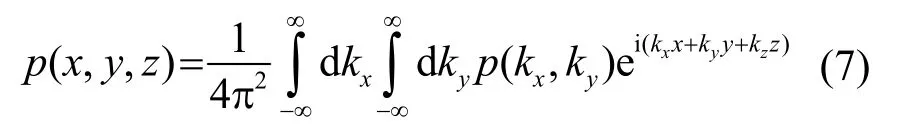
式(7)的包括了从亚声速波到超声速波所有波数的取值。讨论声源均被限定在z≤0的空间里(没有平面波沿着-z轴的方向传播)的情况，只取正的kz值。在式(7)中，如果z=0，有

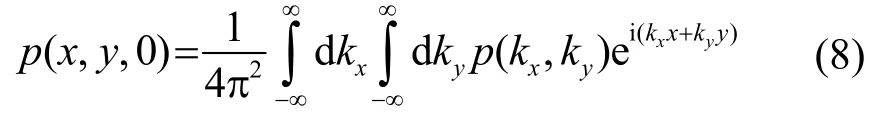
式(8)是无限大平面z=0上的声压表达式。该积分式代表了两个分别关于kx与ky的傅里叶逆变换。复幅值p(kx,ky)的表达式由相应的二维傅里叶变换得出：

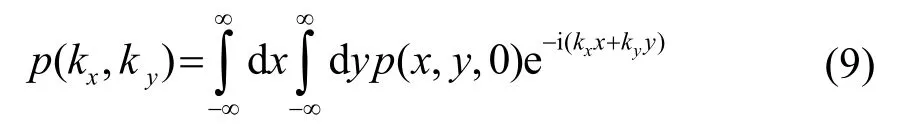
傅里叶变换保证了任意的声压分布p(x,y,0)都可以由式(8)表示。p(kx,ky)称为角谱。角谱法的基本思想就是将波分解成无数个平面波，通过平面波的叠加来计算声场的传播。

2.2 角谱法计算圆形活塞声源近场声压

在近场范围内，声源在任何平面上的声场都可以通过平面传播波和倏逝波的叠加来得到。

式(7)可进一步表示为

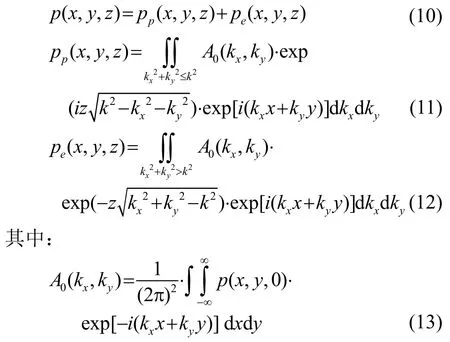
以半径为r0的圆形活塞为例，设声源位于z＝0的xy平面上，可以得到z＝0平面上的声压p(x,y,0)：

2.3 圆形活塞声源声轴线上的声压分布曲线

考虑声轴线上的传播波和倏逝波的分布，则r=0，空间距离z的变化范围为0～1 m。此时，式(17)、(18)可写为

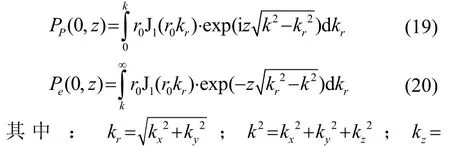
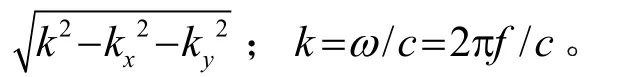
设定圆形活塞声源半径r0=35.0 mm，选取共振频率f=17.1 kHz的声源，c=340 m·s-1，则可得k=316.7。利用数值积分方法，可得圆形活塞声源声轴线上的声压分布曲线，如图3所示。

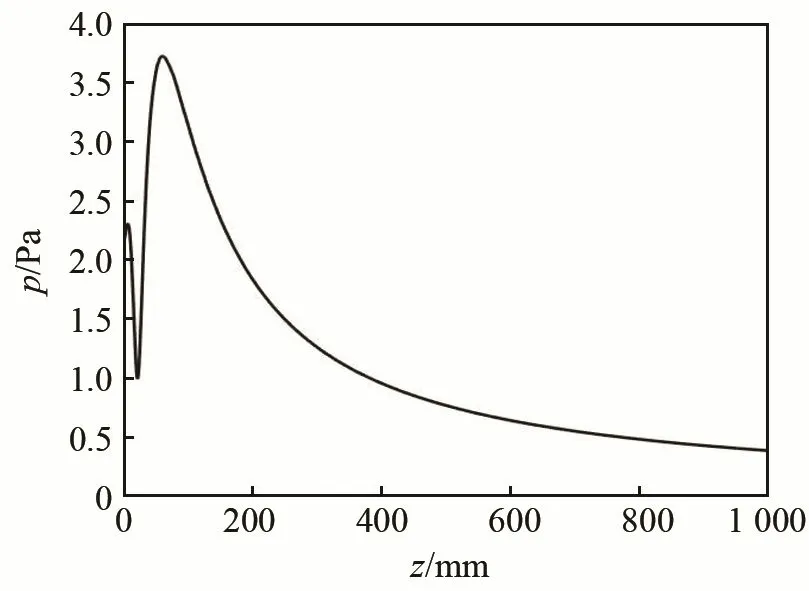
图3 圆形活塞声源声轴线上的声压分布曲线Fig.3 The sound pressure distribution curve along the sound axis of circular piston

由图3可见，在zd=61.0 mm附近图像出现最后一个极值点，可判定此点即为近远场的分界点，zd即为圆形活塞声源的近远场临界距离。

2.4 点源组合法计算近场声压

以半径为r0的圆形活塞为例，设活塞速度为u=uaejωt。我们用点源组合法解决该声源的辐射问题[15]。将声源划分成许多微元，微元上所有点源到达待测点时，其振幅相等、相位相同，将所有微元的声压贡献叠加起来可以得到声源的总声压：

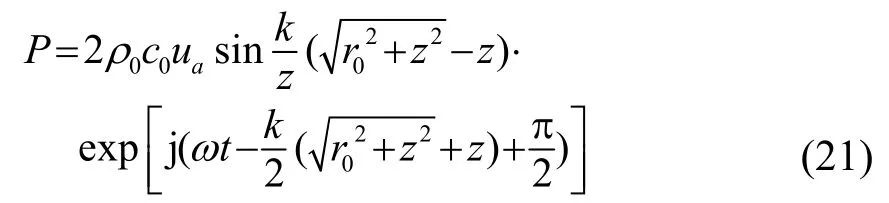
式中：ρ0为声源静态密度；c0为声速；ua为质点振速幅值，k为波数，r0为圆形活塞半径，z为待测点离开活塞中心的距离。令：

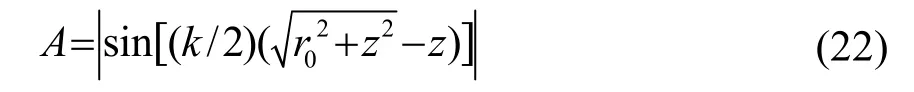
式(22)描述了声轴线上的声压振幅随距离z而变化的规律。

将式(22)展开成级数，经计算，当zg=r02/λ时，声压振幅为最后一个极大值点，且当zg＞r02/λ时，声压振幅随距离z反比的衰减。最后一个极大值的位置可以看作活塞辐射近场过渡到远场的分界线，因此zg也可称为活塞声源的近远场临界距离。以半径为35.0 mm，共振频率为17.1 kHz的圆形活塞声源为例，代入数据计算可得，本算例中：zg=r02/λ=61.8 mm。

由以上分析可知，由角谱法计算得到的声压分布曲线中近远场分界点与点源组合法所得结果一致。

2.5 不同声源半径时、不同辐射频率下声压分布曲线的比较

由式(19)、(20)可知，圆形活塞声源声轴线上的总声压还与声源半径r0有关。设定共振频率不变(20 kHz)，选取半径不同的声源可以得到声场中总声压与声源尺寸的关系，结果如图4所示。圆形活塞声源声轴线上的总声压还与声源的频率大小有关。设定声源半径不变，不同辐射频率下声场中总声压的变化关系如图5所示。

从图4可以看出，声压幅值随着声源半径的增大有所增加，近远场临界距离随着声源半径的增大而增大。从图5可以发现，声压幅值随着辐射频率的增大有所增加，近远场临界距离随着辐射频率的增大而增大。

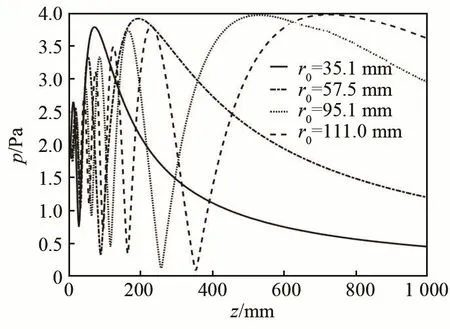
图4 圆形活塞不同声源半径时声轴线上的声压分布曲线Fig.4 The sound pressure distribution curves of circular pistons with different sound source radius

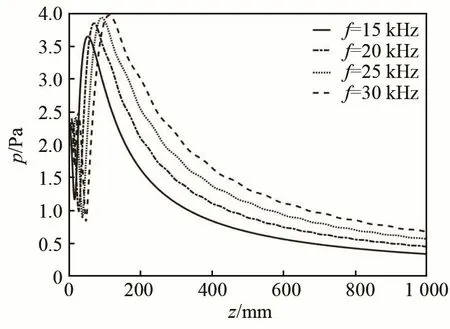
图5 圆形活塞声源不同辐射频率下声轴线上的声压分布曲线Fig.5 The sound pressure distribution curves of circular pistons at different radiation frequencies

3 实验测试

由于辐射平圆盘的振动节线两侧相位相反，所以将辐射圆盘表面改进为阶梯圆盘，即在平圆盘的节线上直接竖起阶梯，阶梯高度为声波在辐射介质中的1/2波长，这样可以避免相位相反的相消干涉。文献[16]提出，阶梯盘的辐射理论上应等于对应活塞的辐射，即阶梯盘是活塞式辐射器。文献[17]进一步验证了这一结论，用解析法计算的指向性图与其相应的活塞的指向性图相当。现用阶梯圆盘代替圆形活塞进行实验。

设计了一个45#钢材的单阶梯圆盘，尺寸参数如表1所示。其中f为弯曲振动频率，h1和h2分别为阶梯圆盘的厚度和基底厚度，a和r分别为阶梯圆盘的半径和节线半径。材料参数为：材料密度ρ=7.8×103kg·m-3，泊松比σ=0.28，弹性模量E=2.16×1011Pa。

表1 单阶梯圆盘的尺寸参数Table 1 Dimension parameter of the stepped circular plate with a single step

实验测试装置如图6所示。将阶梯圆盘嵌在大尺寸塑料挡板中，使之与前后方的媒质隔开。超声波发生器激励纵振换能器，阶梯圆盘中心与换能器相连，圆盘作弯曲振动。阶梯圆盘的中心与麦克风保持在同一高度。前置放大器与麦克风相连的精密噪声分析仪可以测试所在位置处的声压级值。改变麦克风前端与阶梯圆盘中心的距离，使之在5.0～1 000 mm间变化(由于测试过程中换能器与阶梯圆盘用有一定高度的螺母连接，因而无法从0 mm处开始测量)，并记录对应位置的声压级。将声压级换算后得到声压的值。

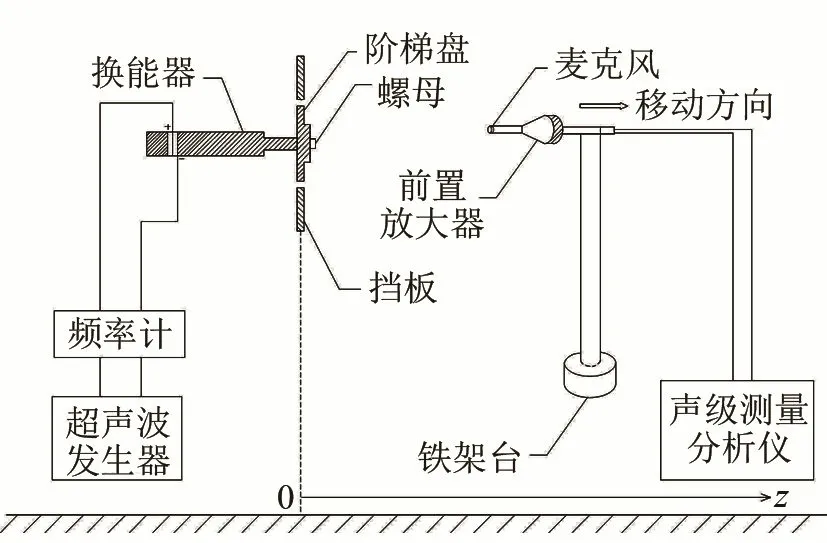
图6 实验测试装置图Fig.6 Testing apparatus diagram

实验仪器为精密噪声分析仪NA-42(测量频率为1 Hz～100 kHz)，前置放大器NH-5A(灵敏度为0.9 V·Pa-1)，传声器uc-29的口径为1/4in(1in=2.54 cm)、测量频率为20～100 Hz、灵敏度为0.0042 V·Pa-1)。

阶梯圆盘的共振频率为15.7 kHz，实验所用换能器的共振频率为19.8 kHz，复合振动系统的共振频率为17.1 kHz。按照如上测试方法，经测试可得单阶梯圆盘声轴线上的声压分布曲线。利用角谱法结合数值积分方法，与算例对应的圆形活塞声源半径为35.0 mm，可得圆形活塞声轴线上的声压分布曲线，如图7所示。为比较声场轴向方向上的声压随距离变化的理论计算曲线和实验测试曲线的趋势，分别以两者中的最大值作为分母对两者的曲线作归一化处理。从图7可以看出，实验测试结果与理论计算结果的趋势基本吻合。

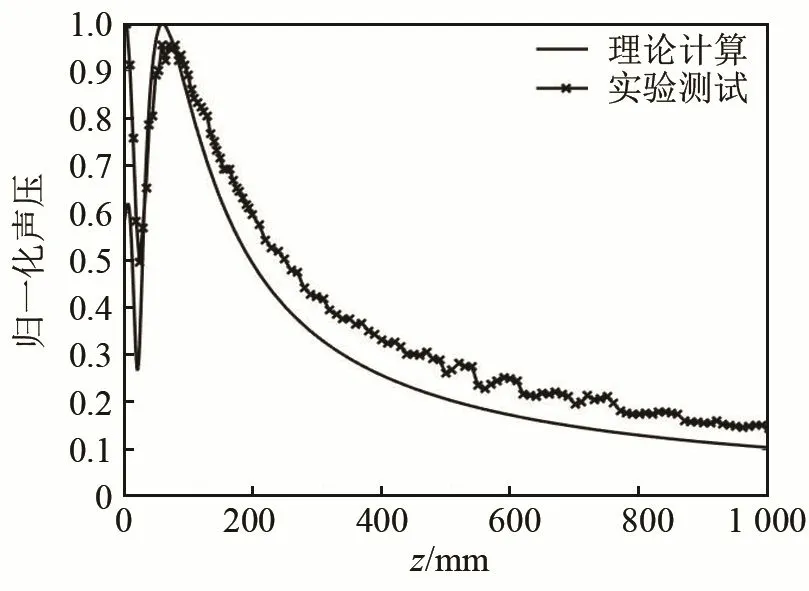
图7 理论计算与实验测试对比图Fig.7 Contrast chart between theoretical calculation and experimental test

4 结 论

利用角谱法可以求得声源近场范围内辐射声场的传播波和倏逝波的分布，结合数值分析方法，可以得到相应的近场声压分布曲线。选定声源半径及频率，经计算得到声源的声压分布曲线，发现用角谱法与点源组合法计算得到的近远场分界点一致。通过对不同声源半径、不同辐射频率下的声压分布曲线进行比较，可以发现声压幅值随着声源半径的增大有所增加，近远场临界距离随着声源半径的增大而增大；声压幅值随着辐射频率的增大有所增加，近远场临界距离随着辐射频率的增大而增大。经测试，实验测试结果与理论计算结果的趋势基本吻合。