基于平板电极的半球谐振陀螺全角技术研究
2020-07-07蒋春桥谭品恒方海斌卜继军
蒋春桥, 江 黎,谭品恒,方海斌,卜继军
中国电子科技集团公司第二十六研究所, 重庆 400060)
0 引言
半球谐振陀螺(以下简称:半球陀螺)是一种固态哥氏振动陀螺,具有结构简单、可靠性高等特点。在20世纪80年代,以美国Litton公司的产品为代表的半球陀螺在宇航领域得到成功应用。这种工作在力平衡模式(速率模式)下的半球陀螺具有高精度的优点,但测量范围有限,带宽较低,限制了其更广泛的应用。近年来,法国Sagem公司研制的工作在全角模式(速率积分模式)下的半球陀螺,以其高动态、大带宽、比例因子稳定等特点,而被广泛用于战术武器、舰船等领域。
国内半球陀螺的研究工作始于20世纪80年代,研制的半球陀螺工作在力平衡模式下,相应产品已成功应用于宇航领域[1],在导弹领域的应用尚处于研究阶段[2]。近年来,国内一些研究单位也开始了半球陀螺的全角模式研究,尚处于起步阶段。本文对半球陀螺全角工作模式的振型控制和信号解算方法进行了研究。使用8个电极,采用时分复用的方式完成了全角模式振型控制和信号解算,并在FPGA+DSP的系统上进行了实现。实验结果表明,两件套半球陀螺样机的测量范围达±400 (°)/s,陀螺最大系统漂移为20 (°)/h。
1 半球陀螺敏感器件
半球陀螺敏感器件由半球型谐振子和平板电极组成,如图1所示。谐振子和平板电极均由具有高品质因数(Q)值的石英材料通过精密磨削加工成型,并在表面进行金属化处理。在平板电极上切割形成等角度分布的8个电极,用于谐振子的驱动和检测。谐振子和平板电极通过精密微组装工艺装配在一起,保持谐振子唇口平面与平板电极间微小的间隙,由此形成平面电容,通过在谐振子和电极之间施加不同的电压形成静电力驱动谐振子振动。通过检测谐振子与电极之间的间隙电容变化来表征谐振子的微振动。装配好的谐振子和平板电极真空封装在金属壳体中,以隔离空气阻尼的影响,保持谐振子的高Q值特性。

图1 敏感器件实物图
2 半球陀螺全角模式原理
当谐振子工作在四波腹模态时,假设外界旋转角度为θ,在惯性力的作用下,谐振子的驻波与平板电极的相对位置会反向旋转αθ。其中α为半球陀螺的进动因子,该进动因子与谐振子的结构形式有关。当结构形式为理想半球形时,α≈0.277 1。
理想谐振子的振动方程[3]为
(1)
(2)
与二维弹簧振子的传递函数一致,可用二维弹簧的简化模型对球壳的振动进行分析,如图2所示。

图2 二维弹簧简化模型
图2(b)中坐标x和y分别代表0°激励电极和45°检测电极的位置,因此,谐振子的振动方程可简化[4]为

(3)
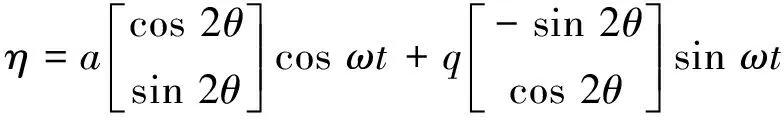
(4)
式中:m为等效质量;c为等效阻尼;Ω为输入角速率;f为外界驱动振子振动的力;Δmc、Δms表示质量分布不均匀;Δcc、Δcs表示阻尼分布不均匀;Δkc、Δks表示刚度分布不均匀。
要使质量分布不均匀和刚度分布不均匀不影响解算出的角度,q必须控制到0[5],令
f=-2maω0[(CrI+CqJ)cosφ+(CaI+
(5)
得到陀螺的传递函数:
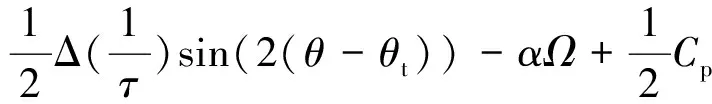
(6)
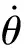
(7)
3 振型参数解算与振型控制
3.1 振型参数解算
两路互成45°的电极的检测信号[6]可表示为
x=acos 2θcosωτ-qsin 2θsinωτ
(8)
y=asin 2θcosωτ+qcos 2θsinωτ
(9)
解算振型参数时,在本地产生参考信号分别为
vrs=2sin(ωτ+δφ)
(10)
vrc=2cos(ωτ+(δφ)
(11)
用vrc、vrs分别与两路检测信号相乘并通过低通滤波器,滤除2倍频信号并完成计算,得到:
cx=vrcx=acos 2θcosδφ-qsin 2θsinδφ
(12)
sx=vrsx=acos 2θsinδφ-qsin 2θcosδφ
(13)
cy=vrcy=asin 2θcosδφ-qcos 2θsinδφ
(14)
sy=vrsy=asin 2θsinδφ+qcos 2θcosδφ
(15)
(16)
S=2(cxcy+sxsy)=(a2-q2)sin 4θ
(17)
Li=2(cxsx+cysy)=(a2-q2)sin 2δφ
(18)
Q=2(cxsy+cysx)=2aq
(19)
(20)
得到驻波方位角、主振动幅度、正交振动幅度、相位误差:
(21)
(22)
(23)
(24)
3.2 振型控制
由于全角模式下驻波在360°内自由进动,因此需要在360°内补充谐振子振动的能量,同时抑制正交振动。平板电极上的电极是等角度分离的8个电极,需要使用独立电极施力的合力对谐振子的振型进行控制,其施力如图3所示,同理可以施力抑制正交振动。
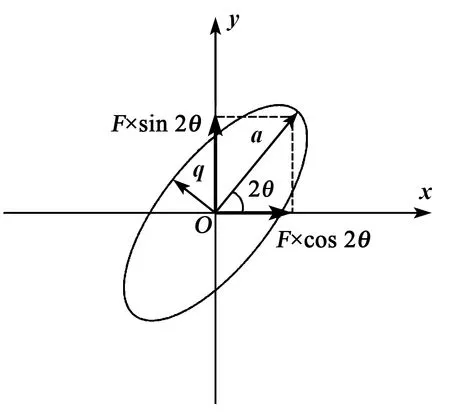
图3 施力分解示意图
4 全角模式振型控制实现与测试
全角模式振型控制电路采用FPGA+DSP的构架实现,其原理框图如图4所示。
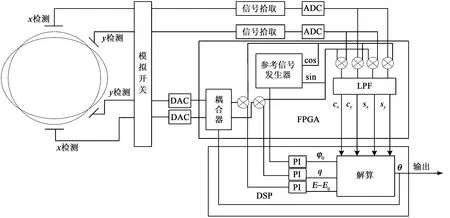
图4 硬件系统原理框图
在FPGA内部完成解调、参考信号生成、控制信号合成,在DSP内部完成信号解算和PI控制信号生成。FPGA选用Xlinx公司的xc6slx45,DSP选用TI公司的TMS320F28335,搭建的陀螺系统如图5所示。为了降低驱动信号对读出信号的干扰,采用读出和驱动分时复用的方法,对驱动信号进行隔离,检测信号波形如图6所示。为了验证所设计的全角模式下半球陀螺的输出有效性,搭建测试平台对陀螺进行了角度/角速度试验。

图5 硬件实物图
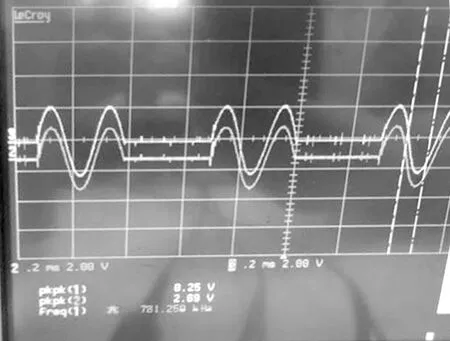
图6 分时复用检测信号波形
在1 (°)/s的转速下,分别使陀螺旋转0°、±30°、±45°和±90°,记录测试数据并对其进行数据处理,如表1所示。对表中的数据用直线函数拟合,得到的比例因子为0.279 4,与理论计算值基本相符,线性度为0.001 4。经分析,线性度较差的原因是陀螺系统存在漂移,导致旋转时间越长,系统漂移对解算角度输出的影响越大。
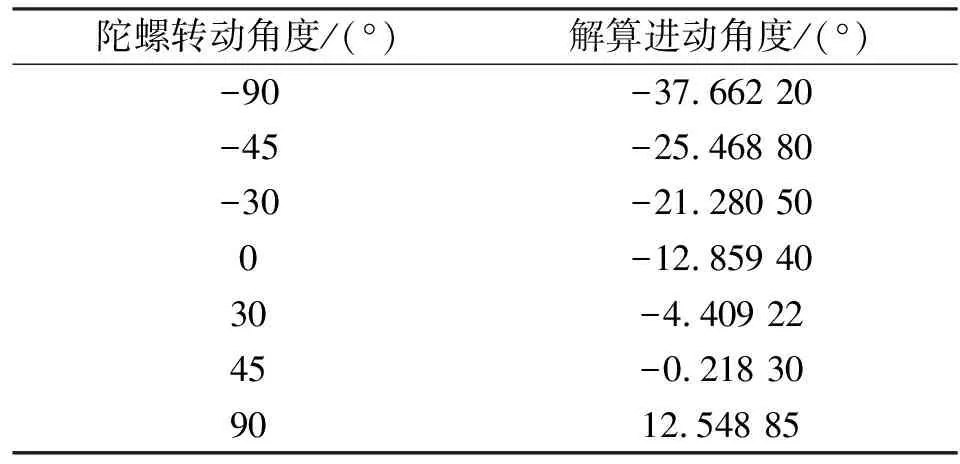
表1 陀螺转动角度和解算角度
分别在±0.1 (°)/s,±1 (°)/s,±5 (°)/s,±10 (°)/s,±50 (°)/s,±100 (°)/s,±200 (°)/s,±400 (°)/s条件下,测试了全角模式半球陀螺的线性度,如图7所示,标度因子为0.275 3,角速率线性度为144×10-6。经分析,引起线性度不理想的因素仍是陀螺系统存在漂移;在0.001 (°)/s的条件下,测试了半球谐振陀螺的阈值,其数据如表2所示,半球谐振陀螺的阈值小于0.001 (°)/s。
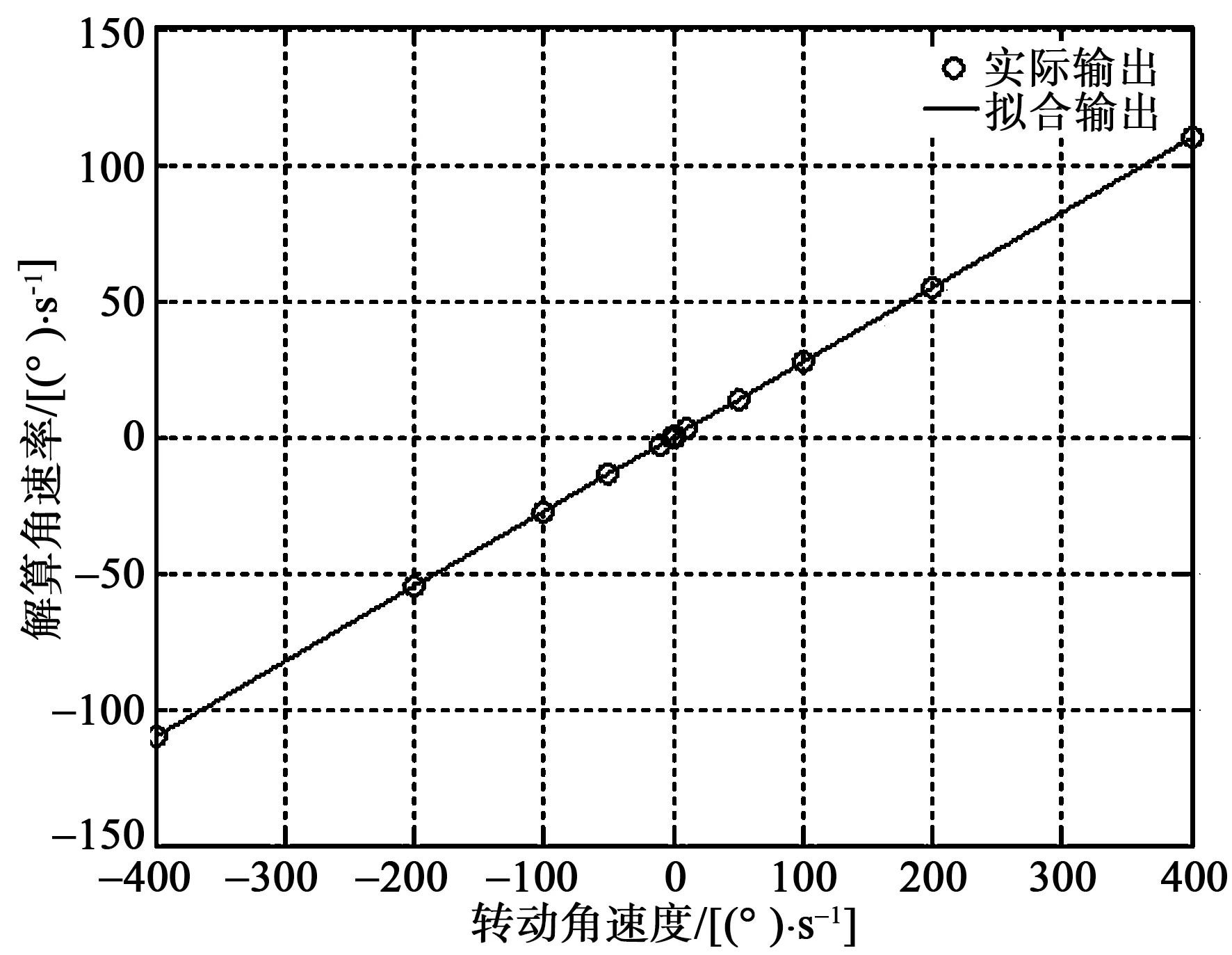
图7 陀螺角速度输出数据及其线性拟合曲线

输入角速率/[(°)·s-1]解算角速率/[(°)·s-1]-0.001-0.003 230-0.002 130.001-0.001 12
对半球陀螺进行长期静态测试,让陀螺敏感轴向指向东,陀螺输入角速率为0,得到驻波角度曲线如图8所示。由图可见,驻波在不同角度下的系统漂移不一致,计入标度因子0.275 3,陀螺指向角度漂移最大值约为6.5 (°)/h。
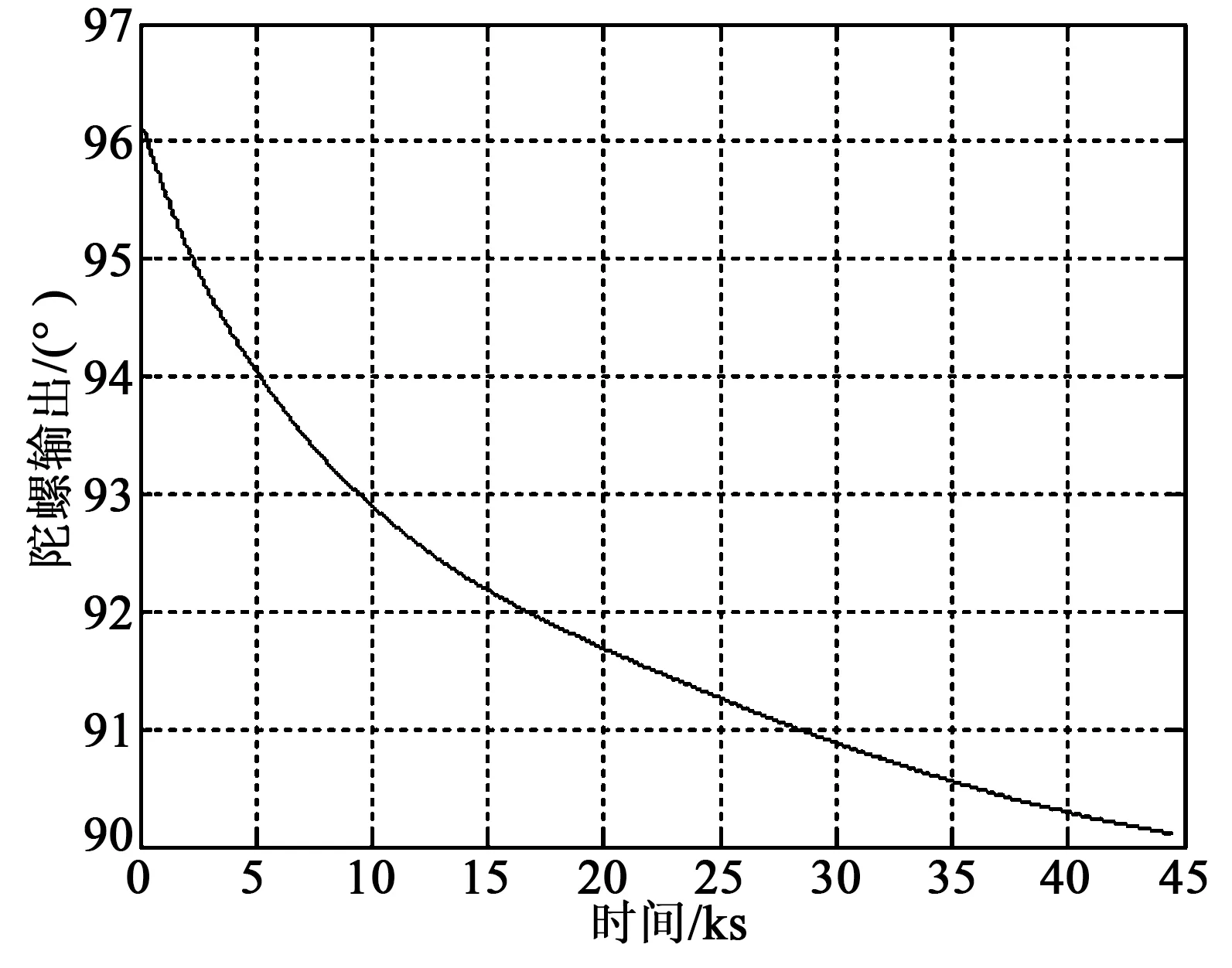
图8 半球谐振陀螺长时漂移测试
为了获取驻波的最大进动角速率,测试了低速转动下陀螺的输出曲线。当转台输入0.1 (°)/s时,测试驻波位置在0°~90°进动时对应的角速率,如图9所示。由图可见,陀螺的角速率输出以90°为周期成正弦分布,且重复性很好,正弦波的峰值约为20 (°)/h,即陀螺的最大系统漂移为20 (°)/h。

图9 半球陀螺系统漂移测试曲线
5 结束语
本文对半球陀螺全角模式进行了研究,介绍了全角模式下半球陀螺的振型解算与驱动,并完成了两件套半球陀螺样机的全角模式系统实现。该系统完成了半球陀螺的稳幅控制和正交抑制,实现了速率积分陀螺的功能;同时,通过微分也能完成速率陀螺的功能。对该系统进行初步测试,得到了该速率积分陀螺的测量范围,零位漂移等指标。相对于力平衡模式,该系统拓宽了测量范围,为进一步提升全角半球陀螺的精度奠定了基础。
