极坐标系下二维各向同性谐振子能级及波函数的研究 ①
2021-01-13张海丰
孙 晶, 张海丰
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
在基础量子力学研究中,二维各向同性谐振子经常被使用,在各个方面都得到了广泛的研究,例如:波函数及概率的可视化演示[1-2];电谐振本征值问题求解[3];双原子分子谐振子模型研究[4];使用MATLAB软件演示线性谐振子能级及波函数[5];含时线性谐振子密度算符的研究[6];涨落质量的谐振子共振行为分析[7];一维线性谐振子非幺正变换研究[8];含时谐振子动力学研究[9];一维线性谐振子能量的不变本征算符法[10];谐振子能级在弱电场中的计算[11];利用作图方法研究一维线性谐振子的波函数和几率密度[12];非对易空间中带电谐振子的能级分析[13];线性谐振子的算符理论分析[14];线性谐振子的能级和不确定关系研究[15];线性谐振子热力学性质研究[16];谐振子的数值计算研究[17]。本文旨在平面极坐标系下对二维各向同性谐振子的能级分布、波函数、简并度、宇称等问题进行详细的研究,并于直角坐标系的结论进行比较,为进一步的理解量子力学本征值问题的代数解法提供理论支持。
1 直角坐标系下的二维各向同性谐振子能级分布和本征矢
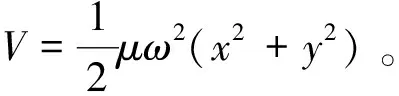
(1)
(2a)
(2b)


(3a)
ψn1(x)=Hn1(αx)e-α2x2/2
(3b)

(3c)
ψn2(y)=Hn2(αy)e-α2y2/2
(3d)

ψn1n2(x,y)=ψn1(x)ψn1(y)
(4)
E=(n1+n2+1)ћω=(N+1)ћω=EN
(5)
式中N=n1+n2=0,1,2,…。易见N,n1,n2满足以下的组合
n1=0,1,2,…,N
(6a)
n2=N,N-1,N-2,…,0
(6b)
所以可以得到能量的简并度为(N+1),且
(-1)n1+n2=(-1)N
(7)
N=0为基态,即n1=n2=0。
2 极坐标系下的二维各向同性谐振子的能级分布和本征矢推导
在直角坐标系和极坐标系下坐标之间满足

(8a)
易得
(8b)
(9)
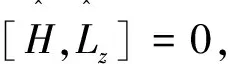
ψ=R(ρ)eimφ
(10)
式中m=0,±1,±2,…。
当坐标做空间反演时,即(x,y)变为(-x,-y),ρ保持不变,但角度φ变为φ+π,所以
ψ(ρ,ρ+π)=R(ρ)eim(φ+π)=(-1)mψ(ρ,φ)
(11)
即ψ(ρ,φ)具有(-1)m的宇称,当m为奇数时为奇宇称,当m为偶数时为偶宇称。所以式(10)所满足的哈密顿方程
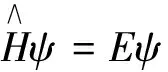
(12)
易见R(ρ)可以表示为
(13)
所以在极值条件下,R(ρ)为
ρ→0,R(ρ)→ρ|m|
(14)
ρ→,R(ρ)~e-α2ρ2/2
(15)
对于非极值的情况表示为
R(ρ)=ρ|m|μ(ρ)e-α2ρ2/2
(16)
所以
ψ=ρ|m|μ(ρ)e-α2ρ2/2eimφ
(17)
所以在极坐标系下,能级为EN,本征矢宇称满足(-1)N,且满足
ρ|m|eimφ=ρ|m|(cosmφ+isinmφ)
(18)
μ(ρ)可以表示成ρ2的n次级数,且
N-|m|=2n
(19)
式中n=0,1,2,…。
取
ε=E/ћω
(20)
ξ=α2ρ2
(21)
所以μ表示为
(22)
当ξ→0时,上式的解为
(23)
式中F=F(a,c,ξ),具体表示成级数为
(24)
取a=-n,即F(a,c,ξ)截取为n次项,所以
(25)
ε=2n+|m|+1=N+1
(26)
E=(2n+|m|+1)ћω=(N+1)ћω
(27)
ψnm(ρ,φ)=|ρ|mF(-n,|m|+1,α2ρ2)e-α2ρ2/2eimφ
(28)
所以N,|m|,n满足以下的组合为
N为偶数时
|m|=N,N-2,…,0
(29a)
n=0,1,…,N/2
(29b)
N为奇数时
|m|=N,N-2,…,1
(30a)
n=0,1,…,(N-1)/2
(30b)
从上边的组合形式可以看出,当|m|≥1,m的取值为|m|和-|m|两个值,即N是偶数和奇数时,都有使得En的简并度为N+1,即极坐标系下的简并度与直角坐标系的相同。
3 结 论
通过以上推导可知,在平面极坐标系下,二维各向同性谐振子的能级为E=(2n+|m|+1)ћω=(N+1)ћω,本征矢为ψnm(ρ,φ)=|ρ|mF(-n,|m|+1,α2ρ2)e-α2ρ2/2eimφ,简并度为N+1,宇称也和直角坐标系的结果一样,即表明坐标系的选取不影响能级分布、宇称、简并度等物理量,而波函数的表示形式大有不同。另外,采用在不同坐标系求解量子力学相关本征值问题对于更好的理解代数解法有很好的理论意义。
