新型自复位延性剪切板支撑钢框架结构基于位移的抗震设计方法
2020-07-07孙国华王枭迪
刘 鎏, 孙国华, 王枭迪
(苏州科技大学 土木工程学院,江苏 苏州215011)
近年来数次强烈地震造成的人员伤亡虽已下降,经抗震设计的结构已实现大震不倒的目标,但震后结构过大的塑性残余变形不仅会使建筑物本身的使用功能中断,还会产生高额的修复费用。 当结构震后的层间残余位移角超过0.5%时[1],修复成本甚至高于重建成本。 自复位结构震后残余变形几乎为零,可实现震后不经修复即可快速恢复使用功能。本课题组在Giannuzzi 博士[2]提出的延性剪切板支撑的基础上,通过将剪切厚板替换为剪切薄板,实现了具有捏缩滞回特征的抗侧力构件,并通过引入镍钛SMA 线材实现了构件的自复位功能,形成了一种新型的自复位延性剪切板支撑(Self-centering Braced Ductile Shear Panel,SC-BDSP)钢框架结构,见图1。 新型SC-BDSP 钢框架结构具有较高的水平承载力和抗侧刚度,震后易于修复,非常适合作为抗震结构的主要抗侧力构件,在地震区具有广泛的应用前景。
传统结构抗震设计方法一般基于强度或承载力进行设计,但结构在地震作用下的破坏程度与位移响应密切相关,采用位移作为指标进行结构设计更为合理,基于位移的抗震设计方法逐渐受到了广大学者的关注。梁兴文等[3]结合我国建筑结构抗震设计的实际,提出了钢筋混凝土结构基于位移的抗震设计方法,通过12 层框架算例设计及时程分析,表明了该方法能够控制结构在不同地震水准作用下的性能。 辛力等[4]考虑高阶振型的影响提出了高层建筑结构直接基于位移的抗震设计方法, 通过某12 层RC 框架结构的算例设计和弹塑性时程分析,表明了高阶振型对结构位移贡献不是很大,但产生的地震作用仍不可忽略。王文达等[5]提出了钢管混凝土结构基于位移的抗震设计方法,设计了12 层的算例,通过静力推覆分析评估了结构的抗震性能,结果表明该方法比传统的承载力设计方法更能保证结构在强震作用下的性能。Malekpour 等[6]提出了不同近断层钢筋混凝土结构体系(纯框架、框剪结构和钢支撑框架)直接基于位移的抗震设计方法,分别设计了三种体系的4 层、8 层和12 层结构算例,非线性时程分析结果表明最大层间侧移均能满足规范要求。 Salawdeh 等[7]提出了一种单层中心支撑钢框架直接基于位移的抗震设计方法(DDBD),进行了该结构足尺的振动台试验及非线性时程分析,验证了DDBD 对结构位移及基底剪力等预测的准确性。 目前,本课题组已完成新型SCBDSP 钢框架结构的试验研究、有限元模拟、简化模型等[8-9],对其基于位移的抗震设计方法尚未展开研究。

图1 新型SC-BDSP 钢框架结构
为促进新型SC-BDSP 钢框架结构在地震区的工程应用, 有效控制SC-BDSP 钢框架结构在罕遇地震作用下的弹塑性行为,亟需建立此类结构的抗震设计方法。 本文明确了新型SC-BDSP 钢框架结构考虑高阶振型影响的基于位移的抗震设计方法,分别设计了5 层、10 层两个算例,并采用弹塑性时程法计算了两个SCBDSP 钢框架算例在罕遇地震作用下的最大楼层位移、最大楼层残余位移、最大层间位移角和层间残余位移角等,评估了新型SC-BDSP 钢框架结构基于位移的抗震设计方法的合理性。
1 基于位移的抗震设计方法
1.1 性态目标
基于位移的抗震设计方法需预先确定结构的性态目标,即结构在不同地震水准下的性能水平,通常以层间位移角或位移延性系数μ 为指标对其进行量化,我国规范也明确给出了结构在多遇及罕遇地震水准下的层间位移角限值。 本文以新型SC-BDSP 钢框架结构在罕遇地震作用后仍能实现自复位功能为目标, 要求SC-BDSP 钢框架结构在此水准下不能超过层间位移角限值,并且其震后的残余层间位移角小于0.5%。 根据用户的不同需求,选择SC-BDSP 钢框架结构在罕遇地震作用下的目标延性系数μ,确定其弹塑性层间位移角限值。
1.2 层间位移角限值
SC-BDSP 钢框架的变形模式与中心支撑钢框架结构相近,均为弯曲型,可参考Byata[10]给出的中心支撑钢框架结构层间屈服位移角的计算方法。 此外,为简化设计,参考文献[9]将自复位延性剪切板支撑等效为交叉杆简化模型,参考文献[10]根据下式确定SC-BDSP 钢框架结构的层间屈服位移角

式中,θy为层间屈服位移角;θy,s为层间屈服位移角的剪切分量;θy,ff 为层间屈服位移角的弯曲分量;α 为支撑与钢梁的夹角;εy,brace为支撑材料的屈服应变;εy,col为钢柱材料的屈服应变;Heff为结构的等效高度;L为跨度。
根据SC-BDSP 钢框架结构的θy和位移延性系数μ,可计算出各层的弹塑性层间位移角限值θu

1.3 初次设计采用的侧移模式
针对SC-BDSP 钢框架结构,初次设计采用倒三角侧移模式

式中,Δi为第i层的楼层位移;Hi为第i层到结构底部的高度。
1.4 理想屈服机构
期望所设计的SC-BDSP 钢框架结构在地震作用下出现理想的屈服机构,分别为支撑先失效,然后梁端形成塑性铰,最后底层柱根部形成塑性铰。 该屈服机构属于有征兆的延性屈服机构,见图2。
当SC-BDSP 钢框架结构形成理想屈服机构时, 结构各层的层间位移角可视为相同,结构的延性和变形能力相对于其他屈服机构更优。 本文以图2 所示的理想屈服机构为基础进行此类结构基于位移的抗震设计。
1.5 等效单自由度(SDOF)体系
将多自由度体系(MDOF)转化为单自由度体系,其等效过程见图3。 在将多自由度体系转化为等效单自由度体系时,通常作如下假定[3]:

图2 理想屈服机构
(1)多自由度体系的地震位移响应与假定的侧移模式相似;(2)多自由度体系与等效单自由度体系的基底剪力相同;
(3)水平地震作用在两种体系上所做的功相等。
根据上述假定,其参数等包括效位移Δeff、等效质量Meff、等效刚度Keff,可按下式计算。

式中,N为楼层数;mi为第i层的质量;Teff为初次设计时采用的等效周期,由Δeff根据弹塑性位移谱求得。
1.6 弹塑性位移谱
通过对我国《建筑抗震设计规范》[11]给出的加速度反应谱转化,可获得SDOF 体系的弹塑性位移谱。 图4给出了由我国规范建议的加速度谱转化得到罕遇地震水准抗震设防烈度为8 度(0.3g)特征周期Tg=0.4 s 的弹塑性位移谱。
1.7 层剪力需求
根据等效刚度Keff和等效位移Δeff计算基底剪力Vb

等效单自由度体系的基底剪力与原多自由度体系的基底剪力相等,按下式计算层剪力Vi
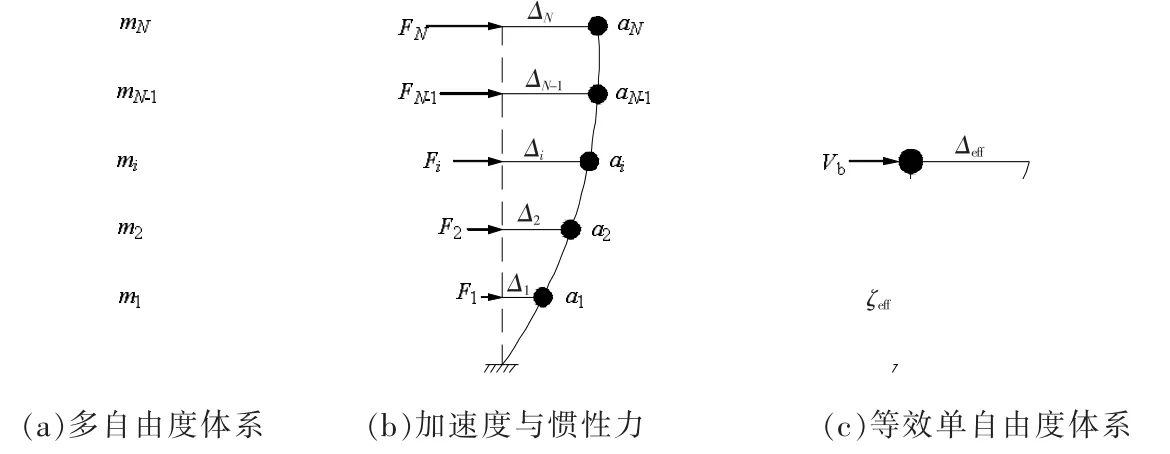
图3 多自由度体系等效示意图
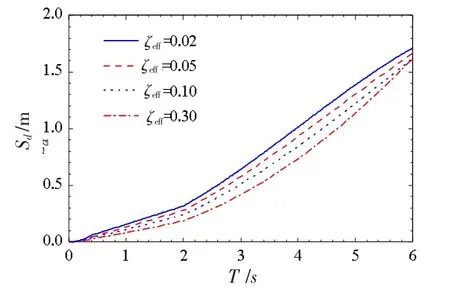
图4 弹塑性位移谱
1.8 高阶振型的影响
高层建筑结构的地震响应受到高阶振型影响较大,基于位移的抗震设计方法应考虑高阶振型的影响。目前,通常将多自由度体系等效为若干等效单自由度体系,对各阶振型的等效单自由度体系分别进行计算,再按SRSS 法进行遇合,得到考虑高阶振型影响的地震作用。 应采用的振型参与数量可通过结构的振型质量参与系数来判定,一般要求考虑高阶振型影响的系数值应大于90%。 振型质量参与系数

式中,Mj为第j振型的模态质量;ψk为k阶振型质量参与系数;k为振型参与数量。
考虑高阶振型影响的结构层剪力Vi计算


式中,Fji为结构第j振型第i层的水平地震力;Vji为结构第j振型第i层的层剪力。
1.9 构件设计
根据我国《建筑抗震设计规范》规定,双重抗侧力体系中的钢框架部分在作为第二道抗震防线时,所承担的抗震剪力应不少于总剪力的25%,支撑部分所承担的剪力应不低于总剪力的75%。 因此,在SC-BDSP 钢框架设计时,应赋予钢框架部分25%的总水平地震作用,结合竖向荷载对其进行设计;将75%的侧向力施加给支撑,考虑抗侧、复位效果,以及延性剪切板与SMA 的合理匹配,进行支撑部分的构件设计。
文献[9]给出了不同尺寸剪切板支撑的受拉和受压水平承载力,剪切板支撑水平承载力Fy,sp

式中,Ft,sp为剪切板支撑受拉方向承担的水平承载力;Fc,sp为剪切板支撑受压方向承担的水平承载力。
SMA 支撑水平承载力Fy,sma

式中,σy为SMA 的屈服应力;Asma为SMA 的截面积。
采用75%的层剪力Vi设计支撑部分

由公式(17)-(19)即可设计SC-BDSP 钢框架的支撑部分。
针对自复位结构的特性,利用OpenSees 软件对所设计的SC-BDSP 钢框架结构进行循环Pushover 分析,检验此时结构各层从2%层间位移角卸载后的层间残余位移角是否满足0.5%的要求; 如不满足, 则需调整SMA 用量。
1.10 迭代设计
迭代设计时,可按以下过程对SC-BDSP 钢框架结构进行设计:
(1)对所设计的SC-BDSP 钢框架结构进行模态分析,得到结构前k阶振型周期,利用弹塑性位移谱由各阶周期Teff,j求得相应的等效位移Δeff,j。
(2)根据等效单自由度体系的等效位移、振型向量计算各阶振型下结构的楼层位移。 第j振型对应的结构侧移模式可表示为

式中,Δji为结构第j振型第i质点的位移;Δjn为结构第j振型的顶点位移;xji为第j振型第i质点的归一化振型幅值;Δeff,j为结构第j振型的等效位移;γj为第j振型的振型参与系数。
(3)利用公式(7)-(8)和公式(14)分别求得各阶振型下结构的等
效质量、等效刚度、基底剪力。
(4)采用SRSS 法遇合,按公式(14)-(16)计算结构的层剪力Vi。
(5)迭代设计得到的SC-BDSP 钢框架结构需进行模态分析,若相邻两次设计的结构基本周期误差小于5%,则设计结束;否则仍需进行迭代设计,直至相邻两次设计的结构基本周期误差小于5%。
1.11 基于位移的抗震设计流程
针对新型SC-BDSP 钢框架结构,采用了考虑高阶振型影响的直接基于位移的抗震设计方法,具体流程见图5。

图5 基于位移的抗震设计流程
2 设计方法的应用
2.1 设计概况
共设计了5 层、10 层两个SC-BDSP 钢框架结构算例,罕遇地震下结构的延性系数为3,跨度及柱距均为6 000 mm,层高为3 600 mm。抗震设防烈度为8 度(0.3g),Ⅱ类场地,设计地震分组为第一组。SC-BDSP 钢框架结构算例的平面布置见图6。SC-BDSP 钢框架结构算例的梁柱节点采用半刚性连接,柱脚为刚接。 钢框架梁、柱的钢材采用Q345 级,自复位SMA 钢支撑所涉及的钢材采用Q235 级,复位功能材料采用镍钛SMA 线材。 为便于有限元分析,采用文献[9]建议的自复位交叉杆宏观模型模拟SMA 自复位延性剪切薄板支撑,算例立面及宏观有限元模型见图7。
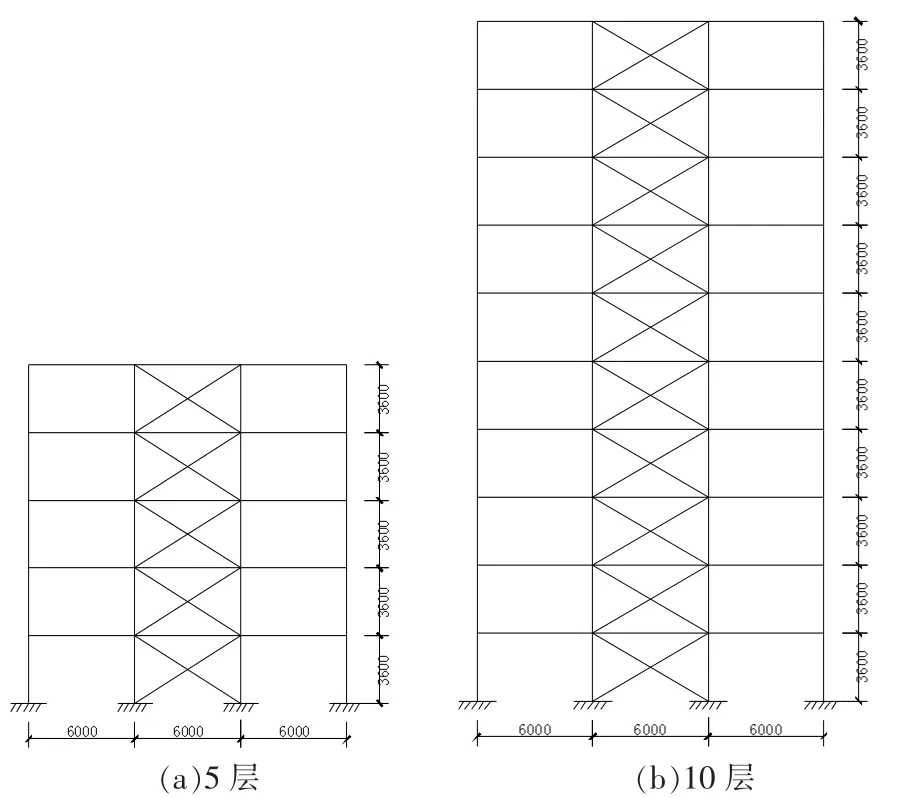
图7 新型SC-BDSP 钢框架结构的立面布置

图6 新型SC-BDSP 钢框架结构的平面布置
在SC-BDSP 钢框架结构算例的数值模拟中,梁柱钢材材性采用考虑强化的双线性模型,并采用随动强化模型考虑钢材的包辛格效应,弹性模量E为2.06×105MPa,后期刚度系数为0.02,屈服强度fy为345 MPa,采用的Steel01 材料本构模型见图8(a);在自复位SMA 钢支撑交叉杆宏观模型中,将剪切板等效为交叉杆,采用的Hysteristic 材料本构模型见图8(b),其中的e1p、e2p、e3p、e1n、e2n、e3n 分别为各关键点应变值,s1p、s2p、s3p、s1n、s2n、s3n 分别为各关键点应力值,算例中不同尺寸剪切板的等效杆参数设置参见文献[9];自复位SMA 钢支撑采用镍钛SMA 材料,其材性取自文献[13],等效模型采用的SelfCentering 材料本构模型见图8(c),其参数取值见表1 所列。

图8 材料本构模型

表1 SMA 等效杆材性参数
2.2 设计过程
限于篇幅,仅给出5 层SC-BDSP 钢框架结构算例的设计过程。 初步设计时,求得5 层SC-BDSP 钢框架结构的层间位移角限值θu=1.59%,根据假定的倒三角侧移模式得到等效位移Δeff=209.73 mm,继而得到等效质量Meff=542.27 t。 根据弹塑性位移谱,由谱位移Sd=Δeff得到对应周期T0=1.92 s。 计算Keff=5 837.60 kN/m,求得基底剪力Vb=1 244.30 kN。 将层剪力Vi分配至各层,初步确定构件截面。 利用OpenSees 软件对SC-BDSP钢框架结构进行模态分析,获得了该算例的前3 阶周期及振型,随后考虑高阶振型影响对5 层SC-BDSP 结构进行迭代设计。 表2 给出5 层SC-BDSP 钢框架结构迭代设计的基底剪力等信息。

表2 5 层SC-BDSP 钢框架结构算例的参数计算结果
根据公式(14)将前三阶振型的设计基底剪力分配给SC-BDSP 钢框架结构的各楼层,计算获得计算榀在前三阶振型下的楼层水平地震力(Fji)及层间剪力(Vji),并通过SRSS 方法获得SC-BDSP 结构总地震作用需求(Vi),见表3 所列。

表3 5 层SC-BDSP 钢框架结构算例的楼层剪力
2.3 截面设计
根据基于位移的抗震设计方法确定了5 层、10 层SC-BDSP 钢框架结构算例的钢柱、钢梁、自复位SMA支撑的截面,见表4 和表5 所列。

表4 5 层SC-BDSP 钢框架结构的梁、柱、支撑截面

表5 10 层SC-BDSP 钢框架结构的梁、柱、支撑截面
3 基于循环Pushover 分析方法的SC-BDSP 钢框架结构复位性能评估
为评估所设计的SC-BDSP 钢框架结构的震后复位功能,采用倒三角水平荷载分布模式对两个结构算例进行循环Pushover 分析,图9 给出了基底剪力-顶点位移角滞回曲线(P-Δ/H)。
由图9 可知,两个SC-BDSP 钢框架结构的整体滞回曲线均呈旗帜形状,具有明显的捏缩特征,虽耗能能力有所降低,但震后复位效果良好。
为更可靠地评估SC-BDSP 钢框架结构算例层间复位效果,图10 给出在最大层间位移角达到2%时的层间位移分布及卸载至零时的残余层间位移角。
由图10 可知,无论是5 层SC-BDSP 钢框架结构,还是10 层SC-BDSP 钢框架结构,在层间位移角出现较大的楼层,所对应的层间残余位移角也相对略大。这说明对于同一结构,该楼层进入塑性程度较深,导致该楼层震后复位能力降低。5 层和10 层SC-BDSP 钢框架结构在最大层间位移角2%卸载至零时的最大残余层间位移角分别出现在第4 层和第6 层, 分别为0.15%和0.27%, 满足了自复位结构层间残余位移角不超过0.5%的要求。
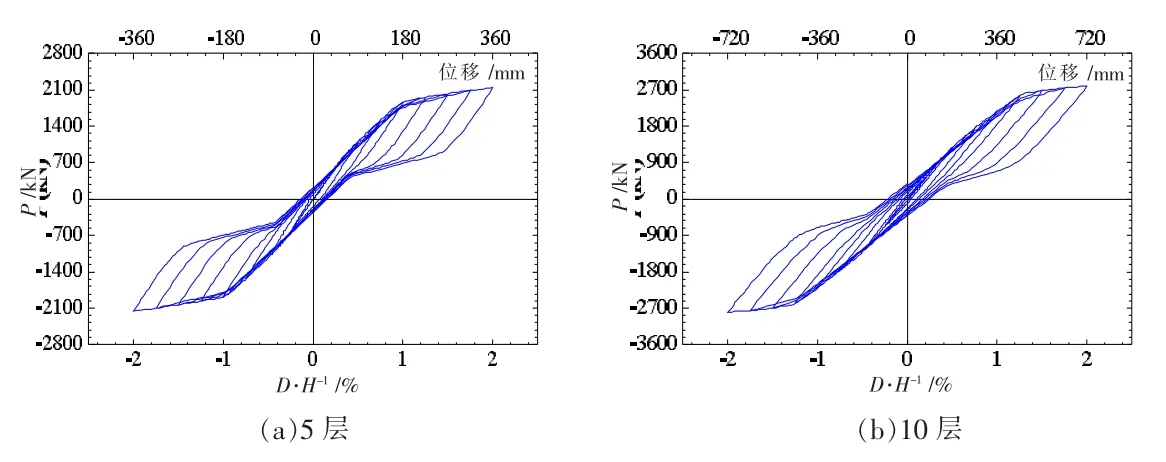
图9 基底剪力-顶点位移角滞回曲线

图10 层间位移角及残余层间位移角分布
4 基于动力弹塑性时程法的新型SC-BDSP 钢框架结构抗震性能评估
4.1 地震波的选取
所选取的两组地震波的见表6 所列。 地震波的选取要求调幅后的每条地震波在结构基本自振周期处的谱加速度值与对应的规范谱加速度值的误差小于35%,调幅后多条地震波在结构基本自振周期处的平均谱加速度值与对应规范谱加速度值的误差小于20%。 通过对大量实际地震波进行分析筛选,最终为SC-BDSP钢框架结构算例选择了符合要求的20 条地震波,每组20 条地震波调幅后的Sa谱和平均Sa谱见图11。图11可知,地震波的谱曲线具有明显的离散性,充分体现了地震波的随机性。 总体上,所选择的两组20 条地震波的Sa谱与规范谱值在结构基本自振周期处拟合较好,能满足要求。 图12 给出了两组地震波对应于罕遇地震水准在结构基本自振周期处的谱加速度值与规范谱的对比。 调幅后的每条地震波在结构基本自振周期处的谱加速度值与规范谱误差均小于35%,调幅后的每组地震波在结构基本自振周期处的谱加速度均值与规范谱的误差分别为8.07%和4.59%,均小于20%,满足要求,可用于SC-BDSP 钢框架结构的弹塑性时程分析。

表6 地震波信息

图11 所选择地震波的Sa 谱
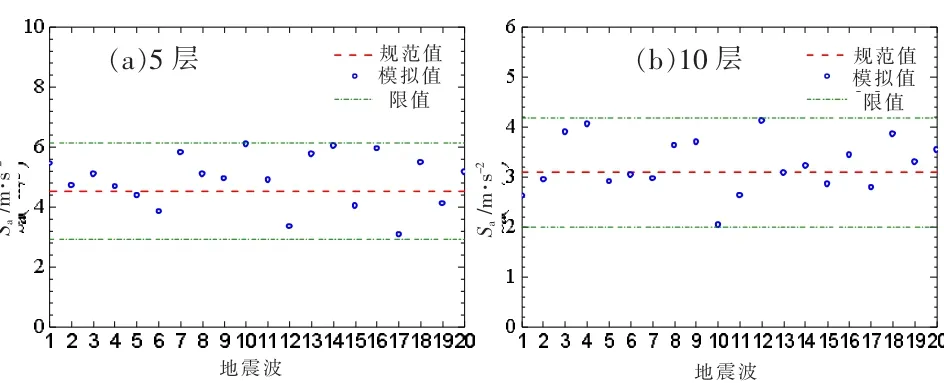
图12 各组20 条地震波Sa 谱的对比
4.2 结果分析
采用有限元程序OpenSees 建立了两个SC-BDSP 钢框架结构算例的宏观动力有限元模型, 对两个SCBDSP 钢框架结构进行了弹塑性时程分析,重点分析了SC-BDSP 钢框架结构算例的最大楼层位移、最大楼层残余位移、最大层间位移角及层间残余位移角等指标。
(1)最大楼层位移。 图13 给出了罕遇地震水准下两个SC-BDSP 钢框架结构算例在各组20 条地震波作用下的最大楼层位移(δmax)。 由图13 可知,在罕遇地震作用下,因为地震波的随机性和差异性,所设计两个结构的最大楼层位移均具有一定的离散性。 5 层SC-BDSP 钢框架结构的楼层位移明显小于10 层结构的楼层位移,说明随着层数的增加结构受到地震作用的影响增大。
(2)最大楼层残余位移。 图14 给出了罕遇地震水准下两个SC-BDSP 钢框架结构在各组20 条地震波作用下的最大楼层残余位移(δres)。由图14 可知,尽管罕遇地震作用下两个SC-BDSP 钢框架结构均产生了较大的塑性变形,但是地震动激励结束后结构的残余楼层变形均较小。 5 层SC-BDSP 钢框架结构的顶点最大塑性残余位移为17 mm,10 层SC-BDSP 钢框架结构的顶点最大塑性残余位移为38 mm。 10 层SC-BDSP 钢框架结构顶点比5 层结构顶点进入塑性程度更深,所以10 层结构顶点的塑性残余变形更大。SC-BDSP 钢框架结构经历强震后,结构楼层虽出现塑性残余位移,但仍可实现震后复位。

图13 最大楼层位移分布

图14 最大楼层残余位移分布
(3)最大层间位移角。 图15 给出了罕遇地震水准下两个SC-BDSP 钢框架结构在各组20 条地震波作用下的最大层间位移角(IDRmax)。 由图15 可知,5 层和10 层SC-BDSP 钢框架结构层间位移角较大值均出现在中上部楼层。底层的层间位移角最小,主要是因为其与地面固接,受到约束较大所致。5 层和10 层SC-BDSP钢框架结构最大层间位移角分别出现在第4 层和第9 层,其均值分别为1.56%和2.10%,与设计时采用的层间位移角限值1.59%和2.22%很接近,进一步证明了本文采用的基于位移的抗震设计方法的合理性。
(4)层间残余位移角。 图16 给出了罕遇地震水准下两个SC-BDSP 钢框架结构在各组20 条地震波作用下的层间残余位移角(RIDR)。由图16 可知,对于同一个结构,层间位移角较大的楼层进入塑性程度更深,其残余塑性变形相对更大。 5 层和10 层SC-BDSP 钢框架结构层间残余位移角均值的最大值分别出现在第4层和第8 层,分别为0.03%和0.05%,完全满足自复位结构层间残余位移角不超过0.5%的要求。

图15 最大层间位移角分布
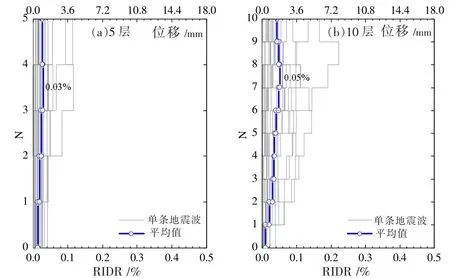
图16 最大层间残余位移角
5 结论
(1)结合我国规范转化的弹塑性位移谱,将考虑高阶振型影响的基于位移的抗震设计方法应用于新型SC-BDSP 钢框架结构;
(2)基于循环Pushover 方法评估按本文建议方法试设计的两个1 榀5 层、10 层SC-BDSP 钢框架结构的复位性能;
(3)采用弹塑性时程方法评估了所设计SC-BDSP 钢框架结构算例的抗震性能,验证了本文采用的新型SC-BDSP 钢框架结构基于位移的抗震设计方法的合理性和可行性。
