约束拉拔植筋锚固性能的试验研究
2020-07-07刘启真唐兴荣
刘启真, 唐兴荣
(苏州科技大学 土木工程学院,江苏 苏州215011)
混凝土结构植筋系统包括混凝土基体、结构植筋胶和植筋钢筋,存在两个接触界面,即植筋胶与植筋界面(简称“胶-筋”界面)、植筋胶与混凝土界面(简称“胶-混”界面)。 由于结构植筋胶与钢筋间的粘结应力要大于结构植筋胶与混凝土间的粘结应力, 一般混凝土结构植筋系统大多发生结构植筋胶-混凝土界面的滑移破坏。 目前,后植筋技术在结构加固中得到广泛的应用,国内外学者针对不同规格的结构胶植筋粘结性能进行了大量的试验研究和理论分析[1-4],但开展对粘结-滑移关系的试验研究和理论分析还不多,且大多通过钢套筒拉拔试验对胶-筋界面粘结-滑移关系进行研究, 对工程实际应用中植筋胶与混凝土界面粘结-滑移的研究还很少[5],因此有必要开展植筋胶-混凝土界面粘结滑移本构关系的研究。 本文以植筋深度、植筋胶厚度、植筋表面特征等为设计参数,进行了7 组19 个单筋约束拉拔试验,研究不同参数对约束拉拔承载力的影响,以及胶-混界面破坏时粘结滑移关系,为植筋结构工程应用和有限元模拟分析提供了技术依据。
1 约束拉拔试验概况
1.1 试件设计
以胶层厚度、埋深深度、钢筋表面形状为参数,设计了7 组19 个混凝土结构植筋约束拉拔试件,各试件参数见表1 所列和图1 所示。 其中第1、2、3、4 组主要对比了不同胶厚的影响,第1、5、6 组主要对比了不同埋深的影响。 第1、7 组主要对比了不同钢筋表面形状特征的影响。
1.2 材料力学性能
各组试件混凝土基体的设计强度等级均为C35,混凝土配合比见表2 所列。实测混凝土立方体抗压强度(150 mm×150 mm×150 mm)为29.7MPa,棱柱体抗压强度(100 mm×100 mm×300 mm)为27.0 MPa。 钢筋HRB400 级,屈服强度为426 MPa,极限强度为612 MPa,弹性模量2.97×104MPa。

表1 试验参数一览表

图1 各试件截面尺寸及配筋

表2 混凝土配合比
结构植筋胶采用国产的鑫球牌植筋结构胶,型号为XQ-360E,植筋胶力学指标如下。
XQ360E 双组份环氧植筋胶:劈裂抗拉强度≥8.5 MPa,抗弯强度≥50 MPa,抗压强度≥60 MPa,钢对钢拉伸抗剪强度≥10 MPa,约束拉拔条件下带肋钢筋与混凝土(C30)粘结强度≥11 MPa。
1.3 植筋工艺
植筋工艺:采用试模浇筑试件混凝土基体并养护成型→采用水钻钻孔→植筋孔打毛、清理→注植筋胶(约植筋埋深的1/2~2/3)→植筋→养护。需要说明,为了防止成孔时电钻的冲击力致使试件混凝土基体开裂,植筋孔采用水钻成孔,并采用钢丝刷进行反复打毛。 由于植筋孔采用对穿设计,为了防止植筋时漏胶,在每个试件下垫一块中间带孔(直径22 mm)尺寸为150 mm×150 mm 木板,并用透明胶带密封。 带肋钢筋植筋
时,为了使植筋胶能够填充满肋间,应将钢筋旋入,同时需保持植筋钢筋的垂直度。
1.4 加载装置
采用苏州科技大学建材试验室的WE-600 型液压式万能试验机进行拉拔试验,采用荷载控制分级加载。 拉拔反力架采用混凝土握裹力试验装置,如图2 所示。
1.5 测量内容及方法
采用YWD-50、YWD-100 位移计测量试件植筋自由端和拉拔端的竖向位移(位移计布置见图2); 采用钢筋应变片测量植筋钢筋的应变;WE-600 型液压式万能试验机测读拉拔荷载等。 位移计及电阻应变片采用DH3821Net 静态电阻采集箱进行采集。

图2 混凝土握裹力试验装置
2 试验结果分析
2.1 主要试验结果
各组试件主要试验结果见表3 所列。 由表3 可见,绝大部分约束拉拔试验发生胶-混界面破坏。
2.2 加载端拉拔荷载-位移曲线
图3 给出了各试件约束拉拔荷载-竖向位移曲线(P-δ)。 由图3(a)到图3(f)变形钢筋的拉拔荷载-竖向变形曲线可见,拉拔荷载-竖向变形曲线呈三阶段模式,见图4。
(1)弹性粘结段:在加载初期,拉拔荷载与竖向位移曲线近似线性变化,拉拔荷载与竖向位移曲线为通过坐标原点的斜直线。

表3 主要试验结果

图3 各组试件加载端P-δ 曲线

图4 胶-混界面粘结-滑移曲线理论模型
(2)滑移段:随着拉拔荷载的增加,试件拉拔荷载-竖向位移曲线开始出现明显的非线性,在曲线上出现较为明显的弯折。 在几何特征上,可以看作为二次抛物线,且抛物线的顶点为峰值拉拔荷载。
(3)摩擦滑移段:当约束拉拔试件达到峰值拉拔荷载时,粘结界面应力主要为摩擦力,拉拔荷载-竖向位移曲线呈直线下降段。
2.3 拉拔承载力分析
(1)植筋胶厚度对拉拔承载力的影响。 试件PBAC-1 至PBAC-4为其他条件相同,植筋胶厚度分别为3.5、2.5、4、5 mm,其峰值拉拔荷载分别为87.5、85.3、90.5、92.5 kN,峰值拉拔荷载对应的位移分别为1.22、1.06、1.31、1.37 mm。图5 给出峰值拉拔荷载-植筋胶厚度关系曲线(Pu-ts)。随着ts增大,植筋胶与混凝土界面接触面积增大,约束拉拔试件的Pu提高,Pu对应的竖向变形增大。
(2)植筋锚固长度对拉拔承载力的影响。 试件PBAC-1、试件PBAC-5 和试件PBAC-6 为其他条件相同,植筋埋深不同,依次为6d、5d、7d,其峰值拉拔荷载分别为87.5、75.5、93.5 kN,峰值拉拔荷载对应的位移分别为1.22、1.21、1.32 mm。 图6 给出了峰值拉拔荷载-植筋相对埋深的关系曲线(Pu-la/d)。 由图6 可见,随着la/d的增大,植筋体系的粘结刚度增大,Pu基本呈线性提高,但峰值拉拔荷载对应的位移没有明显变化。
(3)钢筋表面特征对拉拔承载力影响。试件PBAC-1 与试件PBAC-7 为其他条件相同,前者为带肋钢筋,后者为光圆钢筋。试件PBAC-1 发生胶-混界面破坏,而试件PBAC-7 发生胶-筋界面破坏。图7 给出了试件拉拔荷载-竖向位移曲线P-δ。由图7 可见,试件PBAC-1 的峰值拉拔荷载大于试件PBAC-7 的拉拔荷载,峰值拉拔荷载对应的竖向位移要小于试件PBAC-5 的竖向位移。 因此,混凝土结构植筋应优先采用带肋钢筋。

图5 Pu-ts 惯性系曲线

图6 Pu-la/d关系曲线
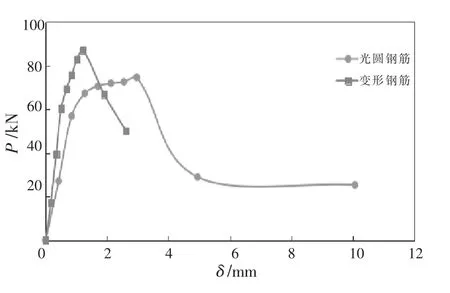
图7 试件P-δ 曲线
3 约束拉拔粘结-滑移特征值分析
(1)极限粘结应力和对应的位移特征值。 平均极限粘结应力τu

式中,Pu为峰值拉拔荷载;D为植筋孔径;la为植筋埋深。
Pu对应的位移值用δu来表示。 由试验结果可知,植筋埋深和胶厚均与呈正相关,则

式中,k1植筋埋深影响系数;k2植筋胶厚影响系数;b基准常系数。 拟合后k1=0.005,k2=0.14,b=0.13;得

试验实测峰值拉拔荷载对应的位移值与按式(3)计算的峰值拉拔荷载对应的位移值的比值的平均值为1.0059,均方差为0.0415,可见符合较好,可以用来计算峰值拉拔荷载对应的位移值。
(2)弹性粘结应力及对应的位移特征值。弹性粘结应力τe为粘结阶段峰值拉拔荷载对应的胶-混界面平均粘结应力。 由试验数据统计得到,τe为极限粘结应力的0.77 倍,即见表5 所列。
弹性位移值δe为弹性阶段峰值点(弹性极限荷载Pe)对应位移,δe为峰值拉拔荷载对应的位移δu的0.51倍,即δe=0.51δu。 见表5 所列。

表5 各试件粘结-滑移本构关系特征点
(3)残余粘结应力及对应的位移特征值。 残余粘结应力由破坏位移对应拉拔荷载计算所得,破坏位移取极限位移的2 倍。 由于本文试验无法得到下降段,残余粘结强度的确定结果[5]采用残余粘结强度
考虑到试验数据样本较少,为了保证拉拔承载力的可靠度,取具有一定保证率的胶-混界面粘结应力

式中,τu为平均极限粘结应力,按式(1)计算;δu为平均极限粘结应力均方差。根据试验数据,按式(4)可得τu=7.43 MPa。
根据上述试验回归确定的约束拉拔粘结-滑移特征值, 可以得到胶-混界面破坏粘结-滑移本构模型的基本函数τ(δ),见式(5)。

由平均粘结强度理论对得到的粘结-滑移本构关系基本函数进行计算,可以得到理论拉拔荷载-竖向位移曲线(图3)。 由图3 可见,拉拔荷载-竖向位移曲线(P-δ)理论值与试验值符合较好,可以较好的反映试验拉拔荷载-竖向位移曲线。
4 结论
通过试验得到以下主要结论:绝大部分带肋植筋钢筋试件均发生植筋胶与混凝土之间界面破坏,能够真实反映植筋胶-混凝土界面的粘结滑移; 植筋胶-混凝土界面的粘结应力与滑移的曲线可简化为弹性阶段、粘结阶段和破坏阶段,根据试验结果回归确定的植筋胶-混凝土界面粘结-滑移理论模型可以用于混凝土植筋结构的有限元模拟分析;试验结果表明,在其他条件不变的情况下,随着植筋胶厚的增大,试件拉拔承载力和滑移值均增大;随着植筋锚固深度的增大,试件拉拔承载力大致呈线性增大。
