例谈引导学生数学探究的问题类型

孙晓华

摘要：问题驱动甚至决定着学生的探索、发现活动，把探索、发现活动变成解决问题的过程。在数学教学中，教师应该特别注意提出激发探究欲望的启思问题、反映数学实质的核心问题、突破生成障碍的关键问题、指向“综合与实践”的应用问题。

关键词：数学探究启思问题核心问题关键问题应用问题

新课标的理念强调，数学教学要以学生为主体，引导学生自主探索、发现，以建构、理解数学知识与方法，锻炼、发展数学思维与能力。因此，教师要提供适当的“诱因”，引导学生的探索、发现活动。

“学起于思，思源于疑。”问题便是最重要的“诱因”。问题驱动甚至决定着学生的探索、发现活动，把探索、发现活动变成解决问题的过程。那么，在数学教学中，教师应该提出怎样的问题呢？笔者认为，以下几类问题必不可少。

一、激发探究欲望的启思问题

这类启思问题，重在激发学生的探究欲望，为接下来的探究活动做好情绪铺垫，并提供方向和线索。惊奇是学生探究的强劲动力。所以，教师设计启思问题时，要通过一些看起来很神奇的情境和现象给学生强烈的刺激，让学生产生认知冲突，感到疑惑不解，从而急切地想探索问题背后的原因和本质，解答自己的疑惑。

例如，教学《和与积的奇偶性》一课时，为了引出探究“和的奇偶性规律”的需求，可以這样创设启思问题——

师见证奇迹的时刻就要来临了！请第一组学号是奇数的同学起立。

（5名学生起立。）

师（停顿片刻）哦，那我知道了，如果把他们的学号表示的数相加，和应该是奇数。你们信吗？

（学生半信半疑。然后，站着的学生报学号，其他学生用计算器计算它们的和，发现确实是奇数。）

师说不定是蒙对的呢！再来一次怎么样？索性增加点难度：你们来挑一个组，请学号是奇数同学的起立。

（学生选择第三组，8名学生起立。）

师（环顾片刻）把这一组站起来的同学的学号表示的数相加，和应该是偶数。

（学生迫不及待地报学号，用计算器计算它们的和，发现确实是偶数。）

师老师甚至都不用知道同学们的学号，就判断出了和是奇数还是偶数。这里是不是藏着什么秘密呀？

这时，学生的惊奇感一下子被激发出来了，他们迫切地想知道和是奇数还是偶数会与什么有关，会是什么原因，于是，接下去的探究会带有强烈的动机。

二、反映数学实质的核心问题

核心问题是经过精心提炼的反映教学主题（即数学实质）的问题，通常是关于“是什么”“有哪些要素”“为什么”“从哪里来”“有什么用”“怎么办”“有什么步骤”等的根本问题，指引着理解知识本质、追溯问题本源等基本方向。这类问题往往直接指向教学目标，处于数学探究的核心。

例如，教学《百分数的意义》一课之前，学生对百分数已经有了一定的认识：在生活中见过了，甚至会读、会写了。那么，关于百分数，学生还要学习什么呢？教师可以向学生提出这个问题。凭借已有经验，学生会以问题的形式提出各种想知道（探究）的内容。这时，教师便可以从学生的问题中精选、提炼出三个核心问题：（1）什么叫百分数？（2）百分数有什么用？（3）百分数和分数有什么联系和区别？由此引导学生展开本节课的探究学习。这三个问题的解决便意味着本节课教学目标的达成。

确定核心问题时，除了要注意教学目标之外，还要注意学生的学习起点以及学生的学习可能。

例如，教学《两位数除以一位数（首位不能整除）》一课之前，学生由于有“两位数除以一位数（首位能整除）”的计算经验，已经会模仿着计算了。所以，“怎样算”不再是学生学习的起点问题，“为什么这样算”才是他们亟待解决的。因此，教师可以出示图1，从学生的立场提出问题：在计算加法、减法、乘法的时候，我们都是从个位算起的，为什么到了除法，却要从高位除起呢？

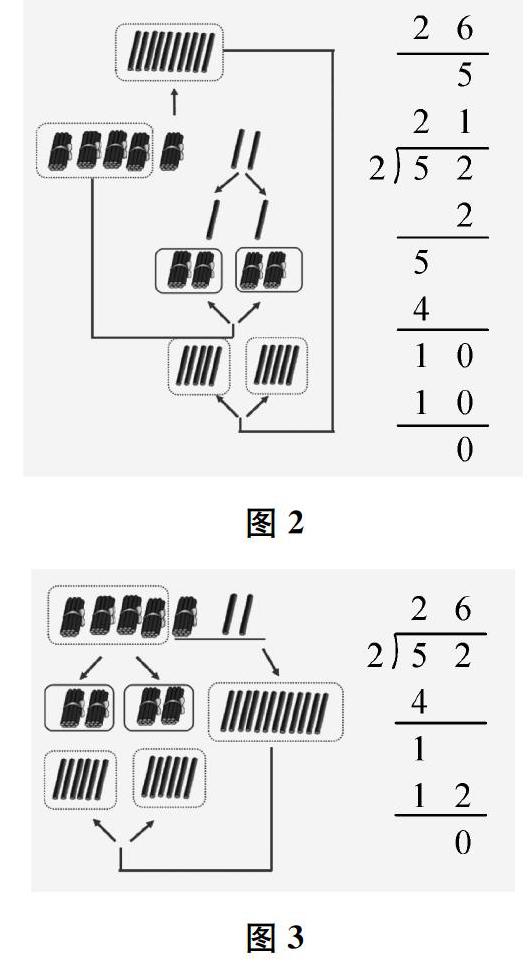
根据原有经验，学生会发现，首位能整除的情况完全可以从个位除起：42除以2，先用个位上的2除以2，商1，再用十位上的4除以2，商2，结果是21。学生感到困惑，于是转向首位不能整除的情况。分小棒和竖式的一一对应，让学生恍然大悟：如图2，从低位算起就是先分单根，再分整捆，这样太麻烦了;如图3，从高位算起就是先分整捆，再分单根，这样简捷很多。通过逐层解析，法理相融，计算教学清晰明了。

三、突破生成障碍的关键问题

顾名思义，这样的关键问题是帮助学生突破学习过程中生成的障碍的问题，通常需要以巧妙的设计，来指引学生思维的转换。它往往指向教学重难点，处于数学探究的关键。

例如，探究“和的奇偶性规律”时，学生在找到两个数和的奇偶性规律后，探索多个数和的奇偶性规律时，一度陷入了迷茫。这时，教师提问：400+28，和是偶数，再加上26，和是奇数还是偶数？再加162呢？如果加的是5呢？学生回答后，教师出示下页图4，进行追问：加数中什么样的数可能改变和的奇偶性？学生回答“奇数”。教师出示图5，继续追问：再来一组，33+127，和是偶数，再加一个什么数，和就变成了奇数？学生还是回答“奇数”。以上设计巧妙的连续问题，引导学生把关注点落到了加数中的奇数身上，相当于在学生探究的道路上递出了一根拐杖，牵引着学生逼近和的奇偶性规律的真相。

四、指向“综合与实践”的应用问题

“学以致用”是学习的高级阶段，它不仅能够激发学生学习数学的兴趣，让学生体会到数学的价值，而且能够巩固和促进学生的数学理解。应用问题主要是与现实生活或其他学科有关的情境问题。教师可以通过应用问题，设计项目化的“综合与实践”活动，引导学生深度学习，发展高阶思维。

例如，从“汽车超速了吗？”这个问题，引出测速仪的功能，继而产生新的问题：测速仪是如何测速的？于是，让学生探寻测速的原理，最终指向研究数学中的速度、时间、路程之间的关系。

再如，“怎样测量比较高的物体（如大楼、旗杆、大树等）的高度？”这个问题，可以调用关于比例的知识，找到相应的数学模型：以同样的焦距拍照，那么，照片中大楼的高度、实际的大楼的高度与照片中门的高度、实际的门的高度具有同样的倍比关系。这样一来，测量照片中大楼的高度、照片中门的高度、实际的门的高度，就可运用比例的知识推算出实际的大楼的高度了。