基于网络嵌入和关联相似性的链路预测算法

冯仁君 陈海雁 王芳

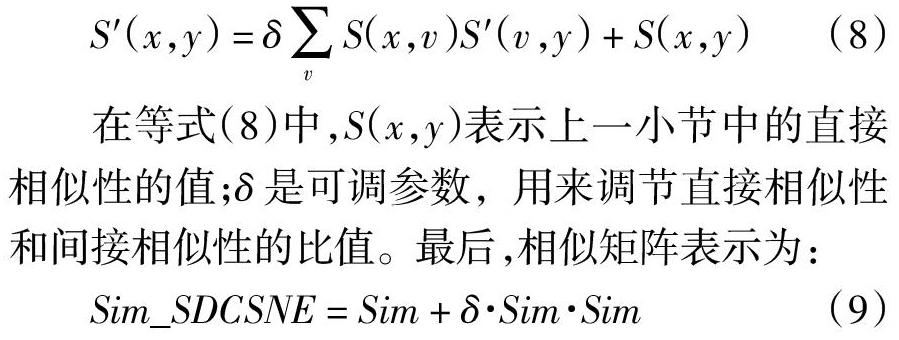
摘   要：链路预测作为复杂网络分析的一个重要分支，在不同领域中有着广泛的应用，而且通过进一步提取网络结构信息可以提高链路预测的精度。提出了一种基于结构深度网络嵌入和关联相似性的链路预测算法（Structural Deep Correlation Similarity Network Embedding，SDCSNE）。SDCSNE算法结合了网络嵌入捕捉高维非线性网络结构的特征，将网络映射到向量空间中，这些映射向量的内积即为对应节点的相似性，并保持了全局和局部的网络结构，获得了更加稳定的网络结构信息;SDCSNE算法还融入了节点的关联性，以提高预测的准确性。实际结果表明，在链路预测任务中，SDCSNE算法具有良好的性能。

关键词：链路预测;复杂网络;相似性;网络嵌入;关联

中图分类号：TP309                                          文献标识码：A

文章编号：1003—6199（2020）02—0114—05

Abstract：Link prediction，as an important branch of complex network analysis，has been widely used in different fields.A link prediction algorithm （SDCSNE） based on structural depth network embedding and association similarity is proposed.The algorithm combines the characteristics of network embedding to capture the high-dimensional nonlinear network structure，and maps the network to the vector space. The inner product of these mapping vectors is the similarity of the corresponding nodes，and maintains the global and local network structure，so as to obtain more stable network structure information.The SDCSNE algorithm also incorporates the relevance of nodes to improve the accuracy of prediction.The practical results show that SDCSNE algorithm has good performance in link prediction.

Key words：link prediction;complex networks;similarity;network embedding;correlation

近年来，复杂网络理论体系不断发展完善，如何利用已有的网络预测缺失或者未来可能出现的关系，分析和探索这些数据的潜在价值已经成为研究热点。该问题也被称为链路预测，对认识和了解复杂网络结构具有重要意义。

复杂网络链路预测问题的研究则是对真实世界网络的进一步剖析。其中，网络由节点和连接节点之间的连边组成，通常情况下，节点可以表示社交网络中的个人、蛋白质相互作用网络中的蛋白质、购买商品的客户等等，连边则表示两个节点之间是否存在联系或者是否发生作用。如果两个节点具有某种特定的作用或者联系则存在一条连边，反之则不存在连边。针对链路预测问题，利用已形成的蛋白质相互作用网络，来预测蛋白质之间未知相互作用[1];在社会关系网络中，朋友之间的关系影响人们社交关系演化以及网络中的用户关系[2-3];根据人们的购物信息形成的电商网络，结合不同的购物风格，从而进行商品推荐以及预测挖掘潜在的客户[4];不仅如此，链路预测方法还在检测和控制网络攻击、交通网络等应用中发挥着重要作用[5]。

链路预测算法使用最为广泛的是基于相似性的方法，因为方法简单、计算复杂度相对较低为人关注，其基本思想是如果两个节点越相似，那么它们之间存在链路的可能性就越大。从网络资源分配的角度来说，有RA（Resource Allocation，RA）指標[6]与AA（Adamix-Adar，AA）指标[7]，均考虑了网络节点度信息，将两个节点之间的资源传递信息量作为相似性指标。基于共同邻居的CN（Common Neighbors，CN）指标[8]，将共同邻居个数作为衡量相似性的标准。在此基础上，考虑到节点度的影响，衍生了Jaccard指标、HDI（Hub Depressed Iindex，HDI）指标等一系列基于局部信息的相似性指标。这类算法因具有高鲁棒性、容易操作的特点，被广大研究者所关注;但此类算法缺乏对未来链路时序性的研究[9]。除了提取结构信息，基于路径信息的相似性指标也是链路预测领域的一大热点。基于路径信息的相似性指标有Katz指标、LP（Local Path，LP）指标[10]。

然而以上方法，均很难选取合适的特征来表示节点的相似性。网络嵌入是学习网络中顶点表示的重要方法之一，目的是捕获和维护网络结构，并且由于其在处理网络数据时表现出优越性，被运用于预测连接中。相似性就可以简单地定义为嵌入向量之间的内积，从而使得基于网络嵌入的链路预测方法无需手动选择网络特征而实现链路预测。有人提出一种结构化的深度网络嵌入方法（Structural Deep Network Embedding，SDNE），利用一阶近似和二阶近似来共同保持网络结构[11]，从而来学习网络的潜在表示。因此，通过适当的网络嵌入，可以很容易地处获取网络的潜在信息，解决链路预测问题。

针对SDNE方法进行改进，在捕捉高度非线性网络结构的过程中，提取嵌入向量并定义为相似度指标，提出了基于结构深度网络嵌入和关联相似性的链路预测算法。

1   相关工作

基于网络嵌入的链路预测方法，首先是利用网络嵌入的方法对方法进行特征相似性的提取，然后是对网络进行重构进而预测新链路。随着数据的不断更新，传统的链路预测方法不再适用，因此，针对选择合适的特征方法不断被提出来。

1.1   深度神经网络

表示学习的表示长期以来一直是机器学习的一个重要问题，许多工作都是针对样本的表示学习[12]。近年来，深度神经网络进行表示学习的研究表明，它们具有强大的表示能力，能够为多种类型的数据提取可靠的特征并且生成强有力的表示。例如，Simonyan等人研究了卷积网络深度对大规模图像识别设置精度的影响[13]。Wang等人提出了一种多模态深度模型来学习图像-文本的统一表示[14]，从而实现跨模态检索任务。

1.2   网络嵌入

较早期有一些关于网络嵌入的相关工作，如局部线性嵌入（Locally Linear Embedding，LocallyLLE）[15]方法，IsoMAP等人[16]首先基于特征向量构造亲和图，然后求解主导特征向量作为网络表示。最近，有人设计了两个损失函数，分别尝试捕获本地和全局网络结构[17]。尽管这些网络嵌入方法取得了成功，但它们都采用了浅层模型，这很难有效地捕捉底层网络中高度非线性的结构。此外，有研究人员利用网络结构的高阶信息[11，18]，尝试使用一阶和高阶邻近性来保存本地和全局网络结构，但是它们分别学习表示，并简单地将表示连接起来。显然，与同时在统一的体系结构中对它们建模相比，同时捕获本地和全局网络结构是次优的。

1.3   链路预测的相似性指标

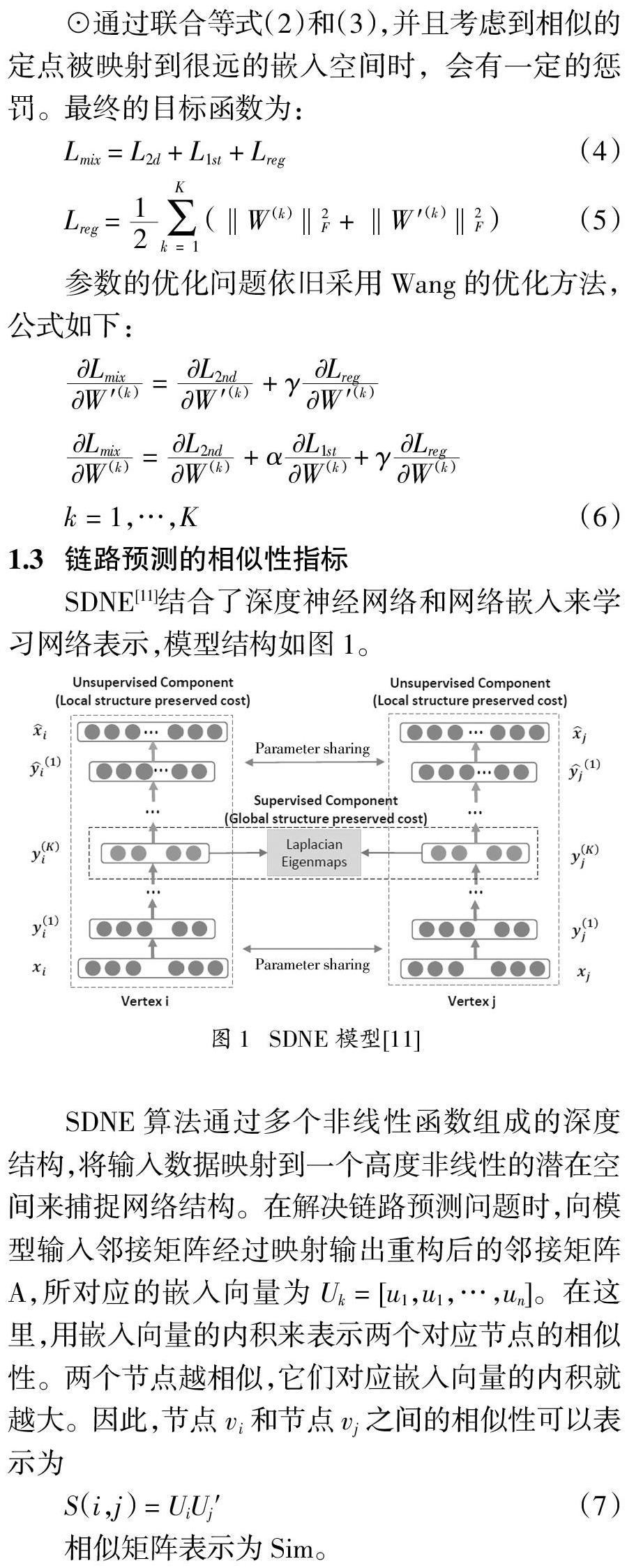
SDNE[11]结合了深度神经网络和网络嵌入来学习网络表示，模型结构如图1。

SDNE算法通过多个非线性函数组成的深度结构，将输入数据映射到一个高度非线性的潜在空间来捕捉网络结构。在解决链路预测问题时，向模型输入邻接矩阵经过映射输出重构后的邻接矩阵A，所对应的嵌入向量为Uk = [u1，u1，…，un]。在这里，用嵌入向量的内积来表示两个对应节点的相似性。两个节点越相似，它们对应嵌入向量的内积就越大。因此，节点vi和节点vj之间的相似性可以表示为

相似矩阵表示为Sim。

SDNE算法提出了一个具有多层非线性函数的半监督深度模型，从而能够捕捉到高度非线性的网络结构。在此基础上，提出了利用一阶近似和二阶近似来共同保持网络结构。其中，二阶近似来捕获全局网络结构，而一阶近似度作为监督分量中的监督信息，以保持局部网络结构。该方法在半监督深度模型中通过一个显式的目标函数联合优化，从而达到既能保持局部网络结构，又能保持全局网络结构的特性。

2   算法设计

2.1   基于网络嵌入的关联相似性改进算法

关联相似性是基于相似的传递性，如果网络中的三个节点x、y、z，其中x与z相似，y与z相似，那么x和y很有可能是相似的，这种相似是间接的，它对网络的影响常常被忽视。x和y的相似性可表示为：

在等式（8）中，S（x，y）表示上一小节中的直接相似性的值;δ是可调参数，用来调节直接相似性和间接相似性的比值。最后，相似矩阵表示为：

2.2   算法建模

为解决复杂网络中的链路预测问题提出了基于网络嵌入和关联相似性的链路预测（Structural Deep Correlation Similarity Network Embedding，SDCSNE）。下面从网络嵌入、关联相似性算法的构建对算法建模进行阐述。

对于网络嵌入方法是基于SDNE算法进行修改。SDNE具有能够捕捉到高度非线性的网络结构，并利用一阶近似和二阶近似来共同保持网络结构，在此基础上提取嵌入向量作为评价相似度的标准。与此同时，考虑到这种表示相似度的方法只关注了节点之间的直接相似程度而忽视了间接间接相似度，为了解决这个问题，提出了SDCSNE方法进行链路预测。

修改SDNE方法后的SDCSNE方法預测链路，如算法1所示。

3   实验及分析

3.1   数据

数据采用Leskovec[19]在一项工作中使用的网络数据ARXIV GR-QC，这是一个论文协作网络。在这个网络中，顶点表示作者，边缘表示作者合作撰写过一篇科学论文。此外，文中还使用了蛋白质相互作用PPI和政治博客网络PB。这三个真实网络数据集用于链接预测任务。

3.2   实验结果

提出的链路预测算法以结构深度网络嵌入方法为基础，该方法首先结合深度神经网络通过自编码器对邻接矩阵进行重构，提取网络嵌入过程中的嵌入向量，定义嵌入向量的内积来表示两个对应节点的相似性。在一阶近似和二阶近似的作用下，嵌入向量包含了全局和局部的网络结构，对应的节点也相应的保留了全局和局部的网络特征，因此用此方法来表示对应的两个节点的相似性。但是此方法忽略了间接相似性的重要性，采取了SDCSNE方法，保证了相似的关联性。

在实验中，引入了@p作为判断算法优劣程度的评估指标，其中@p定义如下：

其中，V是节点集合，index（j）是第j个顶点的排序索引，Δ（i，j）=1表示节点vi和节点vj之间有链接。

首先，对网络GR-QC随机隐藏了15%的链路，并使用@p作为评价指标。图2显示了k值逐步从2增加到1000，对预测精度的影响。当k小于等于500时，精度随着迭代次数的增加始终保持在90%以上，反之，精度低于80%。k值的变化对预测精度的影响如图2所示。

接着，使用三个网络GR-QC、PPI、PB网络进行测试，这三个网络按稀疏程度排序。训练结果如表1。发现网络越稀疏，该算法的预测精度越低，但当k为小于等于100时，预测精度依旧在70%以上。对于此算法，对于一般的网络都可以得到较好的效果，但对稀疏网络在一定条件下才会有不错的效果。链路预测的精度与@P有不可或缺的影响。

实验表明，本文提出的基于网络嵌入和关联相似性的算法可以在真实世界的网络中进行预测缺失或者未来可能出现的链接，并且在稀疏度不同的网络中均可以达到极佳的预测精度。

4   结   论

复杂网络的链路预测具有广泛的应用价值。运用结构深度网络嵌入的方法捕捉高度非线性网络结构，并结合了节点的关联相似性提出了基于网络嵌入和关联相似性的链路预测算法。该方法通过提取提取嵌入向量的内积作为衡量其相似性指标，然后基于相似的关联性，将节点的间接相似性融入网络嵌入方法中。最后，将该算法应用于以上几个真实世界网络中，进行预测网络中已经缺失或未来可能出现的链接。实验表明，该方法具有良好的性能。

参考文献

[1]    YAN Ling-ling，CHEN Zeng-qiang，ZHANG Qing. Analysis of key nodes in China's aviation network based on the degree centrality indicator and clustering coefficient[J].  CAAI Transactions on Intelligent Systems，2016，11（5）：586-593.

[2]    WANG P，XU B，WU Y，et al. Link prediction in social networks：the state-of-the-art[J].  Science in China Series F：Information Sciences，2015，58（1）：1-38.

[3]   HU W，WANG H，PENG C，et al. An event detection method for social networks based on link prediction[J].  Information Systems，2017：16-26.

[4]   MADAN K，YADAV R. Understanding and predicting antecedents of mobile shopping adoption：a developing country perspective[J].  Asia Pacific Journal of Marketing and Logistics，2018，30（1）：139-162.

[5]   CHEN B，CHEN L. A link prediction algorithm based on ant colony optimization[J].  Applied Intelligence，2014，41（3）：694-708.

[6]    ZHOU T，LU L，ZHANG Y，et al. Predicting missing links via local information[J].  European Physical Journal B，2009，71（4）：623-630.

[7]    ADAMIC L A，ADAR E. Friends and neighbors on the Web[J].  Social Networks，2003，25（3）：211-230.

[8]    LIBENNOWELL D，KLEINBERG J M. The link-prediction problem for social networks[J].  Journal of the Association for Information Science and Technology，2007，58（7）：1019-1031.

[9]    張岩庆，陆余良，杨国正. 基于频繁闭图关联规则的AS级Internet链路预测方法[J].  计算机科学，2016，43（Z6）：314-318.

[10]  LU L，JIN C，ZHOU T，et al. Similarity index based on local paths for link prediction of complex networks[J].  Physical Review E，2009，80（4）：1-9.

[11]  WANG D，CUI P，ZHU W，et al. Structural deep network embedding[C]//Knowledge Discovery and Data Mining，2016：1225-1234.

[12]  XU C，TAO D，XU C，et al. Multi-view intact space learning[J].  IEEE Transactions on Pattern Analysis and Machine Intelligence，2015，37（12）：2531-2544.

[13]  SIMONYAN K，ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]//International Conference on Learning Representations，2015，1-14.

[14]  WANG D，CUI P，OU M，et al. Deep multimodal hashing with orthogonal regularization[C]//International Conference on Artificial Intelligence，2015：2291-2297.

[15]  ROWEIS S T，SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science，2000，290（5500）：2323-2326.

[16]  TENENBAUM J B，DE SILVA V，LANGFORD J，et al. A global geometric framework for nonlinear dimensionality reduction[J].  Science，2000，290（5500）：2319-2323.

[17]  TANG J，QU M，WANG M，et al. LINE：large-scale information network embedding[C]//The Web Conference，2015：1067-1077.

[18] RIBEIRO L F，SAVERESE P H，FIGUEIREDO D R，et al. Struc2vec ：learning node representations from structural identity[C]//Knowledge discovery and Data Mining，2017：385-394.

[19]  LESKOVEC J，KLEINBERG J M，FALOUTSOS C，et al. Graph evolution：densification and shrinking diameters[J].  ACM Transactions on Knowledge Discovery From Data，2007，1（1）：1-42.