电容耦合电路对变压器的脉冲频率响应研究

付涛

摘   要：针对电力变压器绕组机械故障在线监测问题，提出了一种在线脉冲频率响应分析（IFRA）对变压器运行进行诊断的方法。建立了电容耦合电路和变压器绕组的等效电气模型，研究了电容耦合电路的频率响应对在线脉冲频率响应的影响。模拟了电容耦合变化和套管介质击穿引起的电容耦合电路参数变化，并研究了它们对在线脉冲频率响应信号的影响。实验结果表明：在低频段内，在线IFRA信号与绕组信号的趋势相反;在中高频段内，在线IFRA信号与绕组信号的趋势存在恒定的差异，且两个信号的共振和反共振位置相同。

关键词：变压器;绕组变形;在线脉冲频率响应分析;电容耦合电路;电气模型;介质击穿

中图分类号：TM417                                    文献标识码：A

文章编号：1003—6199（2020）02—0025—07

Abstract： Aiming at the on-line monitoring of mechanical faults in power transformer windings，this paper proposes a method for online pulse frequency response analysis （IFRA） to diagnose transformer operation，establishes the equivalent electrical model of capacitive coupling circuit and transformer winding，and studies the capacitive coupling circuit. The effect of the frequency response on the online pulse frequency response. The changes of capacitive coupling circuit parameters caused by capacitive coupling changes and casing dielectric breakdown are simulated，and their effects on the online pulse frequency response signal are studied. The experimental results show that in the low frequency band，the trend of the online IFRA signal is opposite to that of the winding signal. In the mid-high frequency band，there is a constant difference between the trend of the online IFRA signal and the winding signal，and the resonance and anti-resonance positions of the two signals are the same.

Key words： transformer;winding deformation;on-line pulse frequency response analysis;capacitance coupled circuit;electrical model;dielectric breakdown

隨着电网容量和负荷的不断增加，变电站的电磁环境变得越来越复杂且故障频繁发生。绕组变形是造成电力变压器故障的主要原因之一，由外部短路电流引起的不平衡电磁力对绕组变形的产生和发展起着重要作用[1]。此外，电力变压器由运输不小心、地震、绝缘材料老化、变压器油中可燃气体爆炸等也是引起绕组机械变形的原因[2]。变压器在绕组变形初期的机械故障对其运行影响不大[3]，绕组变形具有累积效应且机械变形后磁场变化剧烈，外部短路电流引起的强磁场电磁力会超过绕组材料的屈服强度，从而导致进一步的机械故障[4]。此外，损坏的绝缘材料还会产生电热老化，从而导致进一步的短路故障[5]。因此，及时检测绕组变形对防止电力变压器突然失效具有重要意义。

研究了电容耦合电路参数变化对在线脉冲频率响应分析（IFRA）信号的影响。考虑了耦合电容和母线特性阻抗的变化，通过对套管介质击穿失效的模拟，探讨了其对在线IFRA信号的影响。最后进行了验证实验，进一步验证了理论分析和仿真研究。

1   电容耦合电路和变压器绕组的电气模型

1.1   电容耦合电路

所提出的在线IFRA方法简单示意图，如图1所示。利用电容耦合原理，将重复性好、振幅足够大的可控纳秒脉冲注入变压器绕组的端部。特别地，采用电容耦合传感器（CCS），它是一种金属条，包裹在套管外绝缘层周围。同时记录原始励磁纳秒脉冲信号和绕组响应脉冲信号，构造变压器的IFRA信号来估计绕组的状态。

脉冲信号注入方法是通过巧妙地使用变压器套管的配置来实现[6]。变压器绕组的在线IFRA信号实际上不是绕组本身的信号，它包含电容耦合电路的影响将导致绕组信号失真。此外，电容耦合电路的任何参数变化都可能导致在线IFRA信号的变化，最终影响绕组变形的诊断。为了研究这些问题，需要建立电容耦合电路的等效电学模型。在注入高频纳秒脉冲的情况下，可根据电容耦合电路的结构和原理建立电容耦合电路的扰动参数电气模型，如图2所示。

1.2   变压器套管电气模型

在图2b中，将套管的等效电气模型划分为若干个顺序部分，分别由套管电容Cbn、体积电阻Rsn和表面电阻Rpn表示[7]。由于套管层很薄，杂散电感容易被忽略[8]。电容套管层设计为每层电容和电压差相同的结构。套管层电容Cbn的计算公式为：

其中，εr是介电材料的相对介电常数，ln和rn分别是第n层套管的长度和半径。

通过计算同轴圆柱导体的径向电阻公式，可以得到体积电阻：

其中，ρ是电阻率。Rpn是套管层和套管外绝缘介质的表面电阻，通常可以达到106-107 Ω之间。110kV套管由33个电容层组成。文献[9]指出用于电气模拟的套管层数是精度和复杂性之间的折衷。因此，本文采用五层套管等效电学模型作为半测量。此外，电容耦合电路模型的套管分抽头应接地，这是因为当电力变压器投入使用时，套管分抽头应保持接地。

1.3   耦合电容与变压器绕组的有限元分析

采用有限元法（FEM）计算碳纳米管（CCS）形成的耦合电容Cc。根据变压器套管的实际尺寸和材料，建立带CCS的变压器套管的有限元模型，如图3所示。

利用ANSYS Maxwell的静电求解器对套管3D模型进行分析并得到套管的耦合电容。电容计算的基本原理为：

其中，V和We分别是电压源和电场储能，？准是电势分布，Ω是求解域。在110 kV电力变压器套管中，耦合电容Cc的计算值约为30 pF。

本文采用单相壳式变压器绕组等效变压器集总参数电学模型[10]。高压和低压绕组由10个磁片组成。在模型中，每个圆盘由串联电阻Rs和电感 Ls表示，由电容Cs和电导Gs并联。利用介电电导G分流的高压绕组和低压绕组之间的电容CHL模拟了两个绕组之间的绝缘情况，并计算了两个线圈之间的互感Mij。采用电容Cg模拟低压绕组与铁芯之间的绝缘（油），高压绕组与罐体之间的绝缘（油），电容Cg采用介质电导G分流。采用有限元分析工具得到具体的集中参数值，如图4所示。变压器绕组和电容耦合电路的整个电气模型如图5所示。电容耦合电路与高压绕组的终端相连，这是因为变压器工作时总是向高压绕组中注入纳秒脉冲[11]。

2   电容耦合电路对响应的影响

高压绕组端部通过电容耦合电路注入方波脉冲，脉冲宽度为300 ns、脉冲上升和下降时间为30 ns，脉冲振幅为600 V的方波脉冲作为变压器绕组的激励信号Vin，如图5所示。响应电流Io由高压绕组另一端的电流互感器（CT）记录。根据公式（5）-（7），激励信号Vin和响应信号Io构造在线IFRA信号（与电容耦合电路结合的绕组的导纳传递函数）。在这些方程中，fFFT是快速傅立叶变换，用于将时域脉冲信号转换为频域信号[12]。此外，还测量了套管内导体的电压信号Vc，并且Vc和Io都用于构造绕组的IFRA信号（仅绕组的导纳传递函数）：

模拟结果如图6所示。显然，在线IFRA信号与绕组的IFRA信号并不相同。电容耦合电路对在线IFRA信号有重要影响。在0-0.1 MHz頻段内，绕组的IFRA信号呈下降趋势，而在线IFRA信号呈上升趋势。这两条曲线的振幅也有显著差异。在0.1-1 MHz频段内，两个信号的振幅仍有显著差异，这增加了基于信号图形对比诊断绕组变形的难度。在这个频带内，振幅差保持不变，每个共振和反共振的位置都相同。共振和反共振的频率变化最能反映绕组机械故障，这是因为共振和反共振是由分布电感和电容决定：

在0.1 ～ 1 MHz频段内的在线IFRA信号仍可用于绕组变形诊断。

电容耦合电路的频率响应特性如图7所示。该特性相当于纯电容或纯电阻的电容电抗，但以频率响应的形式给出，以便更好地解释IFRA信号。频响信号在宽带频域呈上升趋势。在0-0.1 MHz的低频段内，频率响应呈现出极大的上升趋势，而频率响应更加稳定。电容耦合电路的频率响应趋势对绕组的IFRA信号有明显影响，对0-0.1 MHz的低频段有显著影响。

3   参数变化对响应的影响

3.1   耦合电容变化对在线频率响应信号的影响

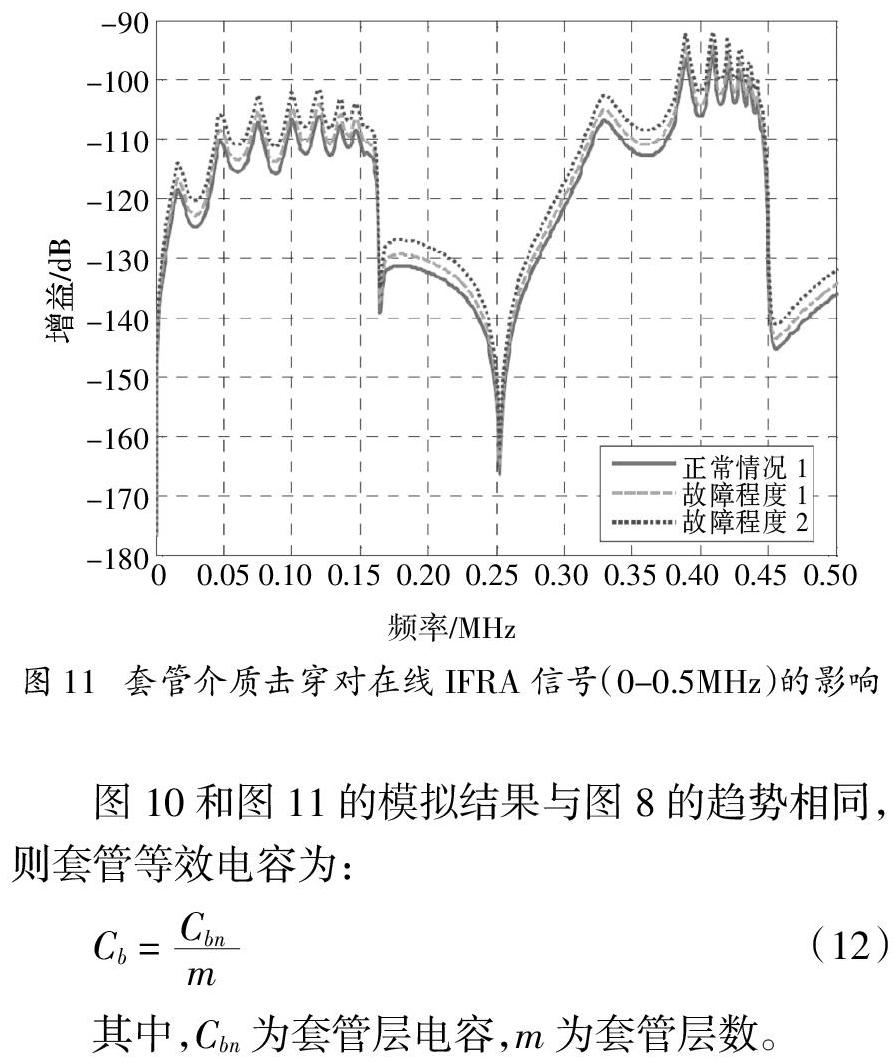
耦合电容Cc是由CCS构成，其实质是杂散电容，其数值可能受某些因素的影响。为了研究耦合电容变化对在线IFRA信号的影响，本文进行了不同耦合电容Cc情况下参数扫描模拟研究。电容Cc设置为10-40 pF时，步长为10 pF。相对于正常值30 pF，最大变化率达到67%。不同条件下的在线IFRA信号如图8所示。

电容耦合电路在不同耦合电容值下的频率响应特性如图9所示。根据图8和图9的结果，耦合电容的变化不会改变在线IFRA信号的形状。然而，由于电容耦合电路的频率响应特性（等效电容电抗）不同，信号的幅度也发生了变化。各频率点的振幅差相同，在不同的耦合电容值下，共振和反共振位置保持不变，这有助于对变压器绕组变形的在线诊断。在实际应用中，由于耦合电容的变化与模拟结果相比不明显，因此，信号的差异并不显著。然而，使用IFRA信号的共振位移和反共振作为在线检测的诊断指标优于使用IFRA信号的幅度变化。

为了获得信噪比较大的响应信号，应采用耦合电容较大的CCS。耦合电容越大，即电容耦合电路的等效电抗越小，从而导致响应电流信号越大，IFRA信号增益越大。

3.2   母线特性阻抗对在线频率响应特性的影响

通过电容耦合电路传输的纳秒脉冲进入母线，考虑到持续时间较短的脉冲，母线的长度可视为无限的。根据Peterson原理[13]，可以用一个集总参数等效电路来代替母线的波传播过程，用其特性阻抗来表示：