基于优化抗干扰自适应算法的变压器有源噪声控制策略分析

蒋健

摘   要：针对传统算法计算不稳定，收敛速度慢的缺陷，提出了一种满足变压器噪声控制的有源噪声前馈控制（GFWC）算法。通过在FIR滤波器中加入构造一个基本函数，采用更少的参数满足算法的收敛性和稳定性，在简化系统的同时保证控制算法系统的稳定性。算法仿真对比分析表明，GFWC算法进行有源噪声控制时，能降低电力设备噪声12～18 dB，远高于传统LMS、NLMS、FxLMS算法。可见，采用有源噪声控制算法为电力设备低频降噪提供了一个有效方式。

关键词：GFWC;变压器噪声;有源噪声控制;参数估计

中图分类号：TP273                                                 文献标识码：A

文章编号：1003—6199（2020）02—0017—04

Abstract：An active noise feedforward control （GFWC） algorithm for transformer noise control is proposed to solve the shortcomings of unstable computation and slow convergence of traditional algorithms. A basic function is constructed by adding FIR filter to the active noise feedforward control algorithm. By adopting fewer parameters to satisfy the convergence and stability of the algorithm，the stability of the control algorithm system is guaranteed while simplifying the system. The simulation and analysis of the algorithm show that the GFWC algorithm can reduce the noise of power equipment by 12～18 dB，which is much higher than the traditional LMS，NLMS，FxLMS algorithm for active noise control. Therefore，the active noise control proposed is adopted.The algorithm provides an effective way for low frequency noise reduction of power equipment.

Key words：GFWC;transformer noise;active noise control;parameter estimation

随着社会经济的发展，大容量电力变压器的使用，在满足用电需求的同时，形成的低频噪声成为困扰周边居民的主要难题之一[1-3]。由于变压器噪声的低频特性，使得传统的被动降噪技术效果并不明显，且价格昂贵。有源噪声控制（ANC）利用次级声源形成与初始噪声相近参数的声波，通过相互叠加来降低空间噪声，因而能满足变压器降噪的目的[4]。目前，相关学者针对ANC技术开展了多方研究工作[5]，如目前应用较为广泛的最小均方Least Mean Square，LMS）算法，具有简单高效的优点，但计算不稳定，收敛速度慢[6];基于LMS算法扩展的归一化最小均方（Normalized Least Mean Square ，NLMS）、滤波-最小均方（Filter-x Least Mean Square，FxLMS）算法等，提高了算法那的收敛速度和稳定性，但在针对小信噪比信号中，一旦受到噪声干扰，则易出现发散问题[7]。基于此，为解决LMS算法存在的上述问题，在传统LMS算法的基础上，提出了一种满足变压器噪声控制的有源噪声前馈控制（Generalized FIR Filter Feedforward Control，GFWC）算法，通过在广义FIR滤波器中加入构造一个基本函数，采用更少的参数满足算法的收敛性和稳定性，在简化系统的同时保证控制算法系统的稳定性。

1   变压器有源降噪系统

1.1   结构组成

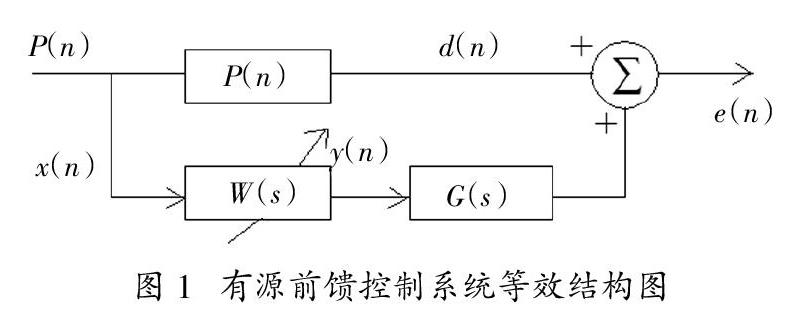
变压器有源噪声控制系统的如图1所示。系统以传感器采集的噪声信号x（n）作为控制器输入参考信号，利用噪声控制算法计算得到系统中次级信号y（n），并以输出的y（n）作为次级声源的驱动信号，误差传感器接受到系统x（n）和y（n）信号，形成误差信号e（n）后，反馈至系统控制器。算法通过对比参考信号和误差信号来实现对控制器参数的调节来改变次级信号强度，直至系统达到稳定状态，获得满足控制目标的信号及参数。

1.2   有源噪声控制算法

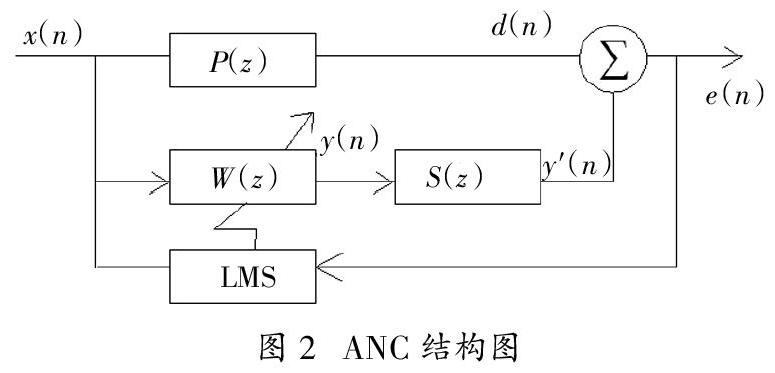
有源噪声控制算法是影响系统稳定性的关键因素之一。自适应算法的实现主要分为处理电路（硬件）实现法以及程序（软件）控制法[8]。在有源噪声控制算法中，需要建立一个精确的次级通道模型来满足权系数矢量更新，这个过程是通过对次级通道辨识实现，因而引入的辨识误差往往对系统的稳定性和收敛速度造成很大影响。如图2是一个典型的FxLMS算法流程圖。