正态模型缺失数据的贝叶斯和Jackknife多重插补法的比较
2020-07-06丁明珠
丁明珠

摘 要:数据缺失是统计调查中经常存在的问题,若是少量缺失则可以利用删除法;若缺失值较多,利用删除法则会丢失大量有用信息,这时候就需利用插补法来补全数据,从而减少对统计分析的影响。根据统计年鉴上近几年的粮食产量、种植规模、有效灌溉面积等系列数据,分别采用贝叶斯多重插值法和刀切多重插值法展开了模拟研究,通过对两种方法所得数据的比对分析,来进一步掌握实际的插值效果。研究发现,利用这两种方法构建的模型都有较好的估计结果,但是贝叶斯多重插补法更为精确,而Jackknife法在操作方面则更为简单。
关键词:贝叶斯多重插补法;Jackknife多重插补法;缺失数据
中图分类号:N37 文献标识码:A
文章编号:1003—6199(2020)02—0119—05
Abstract:Missing data is a common problem in statistical surveys. If there are a few missing,you can use the deletion method. If there are many missing values,the deletion method will lose a lot of useful information. In this case,you need to use the interpolation method to complete the data. Thereby reducing the impact on statistical analysis. This paper simulates the data of grain yield,planting area,effective irrigated area and chemical fertilizer application by using Bayesian multiple imputation method and Jackknife multiple imputation method to compare these two methods in agricultural survey. The study found that the models constructed by these two methods have good estimation results,but the Bayesian multiple interpolation method is more accurate,and the Jackknife method is simpler in operation.
Key words:Bayesian multiple interpolation method;Jackknife multiple interpolation method;missing data
根據实际数据调查结果可知,受技术等多方面要素的限制,往往会出现数据不全面等问题。造成数据缺失的要素来源于多个方面,不同要素造成的数据缺失会引发不同的统计分析偏差。上世纪八十年代,LITTLE与RUBIN结合数据缺失的常见问题以及种类展开了类别探究,对三类缺失数据缺失机制进行了构建。缺失机制包括了完全随机、随机以及非随机三类缺失[1]。而对缺失数据的处理方法通常是删除法,即删除含有缺失值的单元数据。2002年,ALLISON表示如果只有少数的缺失值,那么删除法是可行的,并且具有一定的优势[2]。然而大规模的数据缺失,直接删去不但不利于信息数据的全面掌握,还会导致原本有用信息的参考价值降低,在这种情况下删除法将不再表现出适用性。面对大量的缺失值更可取的方法是插补法,2002年,LITTLE等人又表示相较于删除法,插补法不仅不会丢失原有的数据信息,还能有效地补充数据信息[3]。结合变量存在的关联性展开线性回归模型的有力构建,并基于模型完成对缺失值变量的进一步插补。插补法可以分为单一以及多重插补两类。前者是借助已有的数据进行线性模型参数的预估,随后结合建立完整的模型展开对缺失值的估计。2004年,RUBIN通过研究发现,这类单一插补法会在很大程度上使变量的方差经常被低估,促使整个置信区间狭窄,难以体现确切可信的检验统计量[4]。在此基础上,针对这一问题YING和LITTLE对多重插补进行了运用,强调借助多重插补弥补单一插补存在的系列缺陷。多重插补实现了若干个插补值的同时生成,有助于系统数据集的构建。基于数据集进行未知参数的估计[5]。受缺失值的影响,整个线性模型参数表现出不确定性[6,7],对此可以利用贝叶斯法和Jackknife法对参数进行随机抽取。贝叶斯法的基本思想简单来说就是从后验分布中随机选取插补模型的参数[8],刀切法的基本思想是从原始完整样本的多个刀切样本中获取插补模型的参数[9]。
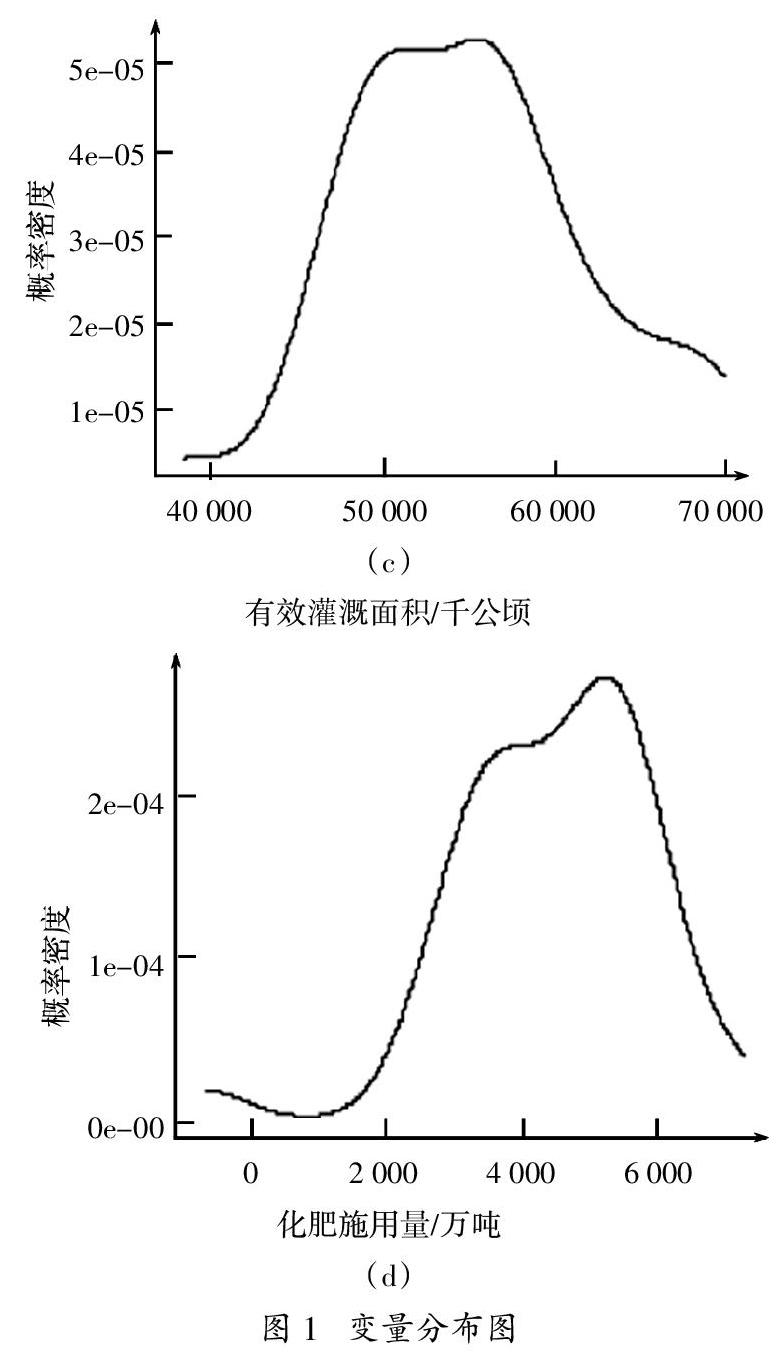
在对插补法的应用研究中,选取了贝叶斯和Jackknife两类多重插补法展开对比分析,选取近年来部分粮食产量数据和完整的播种面积、有效灌溉面积和施肥量数据进行模拟分析,在两种方法支持下展开缺失值的多重插补,再对最终形成的插补参数进行检验对比。所有的数据分析均使用R语言软件。
1 模型的建立
1.1 模型的假设
设Y和X间具有正态线性关联性,即Y ~ N(Xβ,σ2),变量Y具有一部分数据缺失的情况,且缺失表现出随机缺失特性,Y缺失只取决于X,不受自身所干扰,变量X为完整的数据集合,回归系数β为p维向量。
[3] LITTLE R J,RUBIN D B. Statistical analysis with missing data[M].Hoboken:Wiley John & Sons,2002.
[4] RUBIN D B. Multiple imputation for nonresponse in surveys[M]. New York:Wiley John & Sons,2004.
[5] YING G,LITTLE R J. Bayesian multiple for assay data subject to measurement error[J]. Journal of statistical theory & practice,2013,7(2):219-232.
[6] 潘传快,熊巍,祁春节. 正态线形模型下缺失值的贝叶斯多重插补—基于柑橘数据的分析[J]. 华中农业大学学报(社会科学版),2017,000(001):72-77.
[7] 熊巍,潘传快,祁春节. 農业经济调查缺失数据的贝叶斯和Bootstrap多重插补的比较[J]. 统计与决策,2019,35(04):13-17.
[8] SI Y,REITER J P. Nonparametric bayesian multiple imputation for incomplete categorical variables in large -scale assessment surveys[J]. Journal of educational & behavioral statistics,2013,38(5):499-521.
[9] 赵馨,闫在在,魏福红,等. PPS抽样中方差估计的刀切法[J]. 阴山学刊(自然科学版),2011,25(2):20-21.
[10] 李苗. 新时代下我国粮食产量的影响因素分析[J]. 价值工程,2019(14).
[11] 郭燕枝,郭静利,王秀东. 我国粮食综合生产能力影响因素分析[J]. 农业经济问题,2007(s1):24-27.
