一个推广的Hilbert型积分不等式及其逆

刘琼,刘英迪

(邵阳学院 1.理学院；2.经济管理学院,湖南 邵阳,422000)

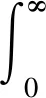
(1)

成立,这里的常数因子π为最佳值。式(1)在偏微分方程理论和分析学中有重要作用[1-2]，经过1个多世纪的发展,式(1)有了非常丰富的推广应用成果,见文献[3-8]。

2011年,杨必成[9]得到1个具指数核的非齐次Hilbert型积分不等式:

(2)

本文引入多个参数,利用权函数方法和实分析技巧,对式(2)进行推广研究，为此考虑了积分核为e-α(xy)β(α>0,β>0)的Hilbert型积分不等式、等价式及相应逆向式,证明了它们的常数因子是最佳值。

1 有关引理

引理1[15]设α>0,β>0,μ>-1,则有下列积分公式:

(3)

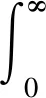
则有

(4)

证明作变换xy=t,由式(3)得到

同理可证得

则有

(5)

(6)

证明很容易证得:

(7)

2 主要结论

(8)

成立。

证明由Hölder不等式[18]和Fubini定理及引理2，有

(9)

定理2在与定理1相同的条件下,还有不等式

(10)

成立,且式(10)和式(8)等价。

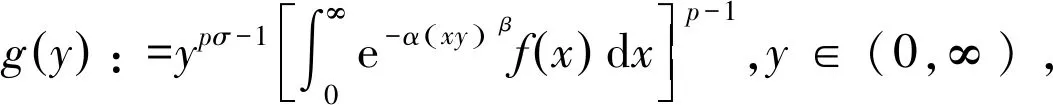
由定理1有

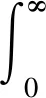
(11)

由式(11)得到

上式两边取p次方即可得式(10)。由式(8)推得式(10)成立。

现在由式(10)推得式(8)成立。由Hölder不等式及式(10)有

上式即为式(8),因此，式(8)和式(10)等价,证毕。

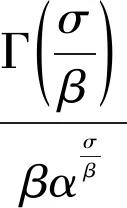
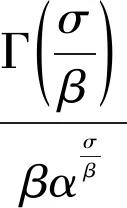
定理4设0

(12)

和其等价式

(13)

成立,且它们的常数因子均是最佳值。

在式(8)和式(10)中选取合适参数值,可得到一些形式简单的不等式。举例如下。

(14)

例2取α=β=σ=1,p=q=2,则得到如下等价不等式:

(15)

(16)

文献[9]也得到与式(15)同样的结论。

(17)

(18)

其中不等式右边常数因子2和4均为最佳值。

(19)

(20)

其中，不等式右边的常数因子均为最佳值。