关于极大外平面图的离心率总和指数
2020-07-06宋玲刘合超汤自凯
宋玲,刘合超,汤自凯
(湖南师范大学 数学与统计学院,湖南 长沙,410081)
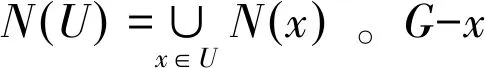
拓扑指数是对分子结构进行数值建模的一种方法,它是通过对特征分子图的矩阵进行一些数字运算而获得的,特征图谱是图的不变量,该图直接在分子结构中生成并反映出该化合物的结构特征。
WIENER[2]介绍了第一个拓扑指数即图G的维纳指数W(G),定义如下:
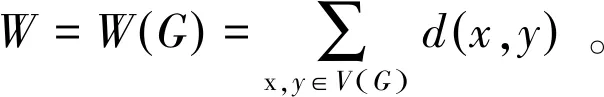
HOSOYA[3]提出一种表征饱和烃异构体性质的指数,并且研究了它与维纳指数的关系。SKOROBOGATOV和DOBRYNIN[4]定义了n个顶点的图的平均离心率为
FARAHANI[5]研究了苯环系统的离心率总和指数,定义如下:
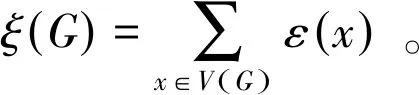
维纳指数和离心率总和指数都是基于距离有关的指数问题。关于维纳指数,人们对各种给定条件的极值问题进行了研究[6-11]。关于离心率总和指数,FATHALIKHANI等[12]研究了离心率总和指数关于图形运算的值的相关问题;DE等[13]研究了合成图的离心率总和指数;SMITH等[14]确定了给定度序列的离心率总和指数的最小化和最大化树的结构;有关离心率的相关其他问题可以参考文献[15-18]。在图论的各种图形结构中,极大外平面图是一种特殊的图形,由于它具有一些特殊结构以及一些非常好的性质,因而引起了许多学者对其进行研究。人们关于极大外平面图的研究一开始大多数主要集中在染色问题等方面。最近,许多人对极大外平面图的一些指数问题进行了研究。HOU等[19]研究了n个顶点的极大外平面图的M1,M2指数上下界并且刻画出了相应的极值图。SU等[20]研究了n个顶点的极大外平面图的一般零阶Randic指数上下界并且刻画了相应的极值图。目前,也有学者研究了给定n个顶点的极大外平面图的维纳指数的上下界问题。
本文研究了极大外平面图的离心率总和指数ξ(G),给出了n个顶点极大外平面图的最小值和最大值并且确定了相应的极值图。在证明中,首先给出了n个顶点的极大外平面图的最小值,并且定义了一种新的图类,接着利用图形变化克服了“最大值中仅仅靠数学归纳法中不能实现”的问题,最后确定了n个顶点的极大外平面图中离心率总和指数的最大值,并且确定了当n为偶数时的最大值在新的图类中达到。
1 预备结论

1)在G中存在1个2度顶点u并且N(u)={v,w};
2)对于任意1点x∈V(G){v,w},vx∈E(G)和wx∈E(G)至少有1个是成立的。

当n=3,4和5时,极大外平面图是唯一的。当n=6时,此时存在3个非同构图(见图1);当n=7时,此时存在4个非同构图(见图2);当n=8时,此时存在12个非同构图(见图3)。并且随着n的增加,非同构图的数目也增加。

图1 顶点数为6时的所有的非同构极大外平面图Fig.1 All non-isomorphic 6-vertex maximal outerplanar graphs

图2 顶点数为7时的所有的非同构极大外平面图Fig.2 All non-isomorphic 7-vertex maximal outerplanar graphs

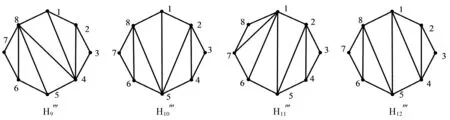
图3 顶点数为8时的所有的非同构极大外平面图Fig.3 All non-isomorphic 8-vertex maximal outerplanar graphs
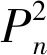

图4 图
在文献[19]中,HOU等给出了极大外平面图的一些性质。
引理1[19]令G为n≥4的1个极大外平面图。若v为G中1个度为2的点,并且其邻点为u和w,则uw∈E(G)且|N(u)∩N(w)|=2。
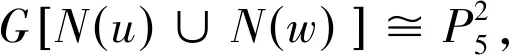
1)G中存在1个点u,满足d(u)=2且N(u)={v,w},d(u)+d(w)=7;

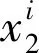


图5 图
根据极大外平面图的定义,可以得到下述事实。
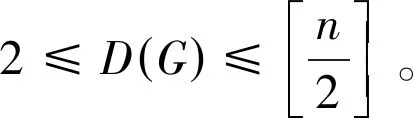
1)若n=6,左边等式取等时当且仅当G≅K1∨P5或者G≅H′2(见图1);
2)若n≥7,左边等式取等时当且仅当G≅K1∨Pn-1;
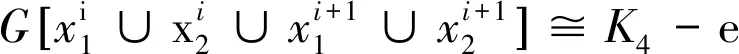
通过直接的计算,可以得到下面的两个结果。
引理3令G为顶点数为n的1个极大外平面图,其中n≥6,则
ξ(K1∨Pn-1)=2n-1,
引理4令G为顶点数为n的一个极大外平面图,其中n≥6。


2 极大外平面图的离心率总和指数的最值
定理1令G为1个顶点数n≥6的极大外平面图,则ξ(G)≥2n-1等号取等时当且仅当G≅K1∨Pn-1。
证明当n=6,H6={H′1,H′2,H′3}(见图1),通过直接运算,可以得到:
ξ(H′1)=11,ξ(H′2)=12,ξ(H′3)=14
这个结论对于n=6时成立。
接着证明当n≥7时也成立。假设这个结果对于阶数小于n的所有的极大外平面图是成立的。设G为1个极大外平面图,并且|V(G)|=n。根据引理1,知道G中一定存在1个顶点u且d(u)=2,N(u)={v,w}。令G′=G-u,那么可以得到G′是1个极大外平面图,并且|V(G′)|=n-1。根据数学归纳法可以得到
ξ(G′)≥2(n-1)-1=2n-3。
由事实1可以得到对于任意的vi∈V(G)有ε(vi)≥2成立。令G′=G-u,得到εG(vi)-εG′(vi)≥0。则
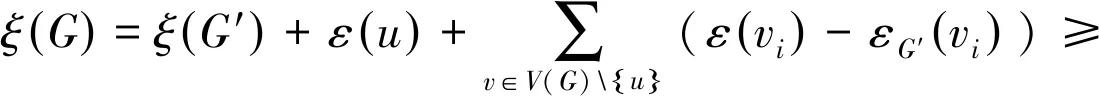

令G为1个阶数为n的极大外平面图,u为1个2度顶点且N(u)={v,w}。由引理2,可以得到d(v)+d(w)≥7。
引理5令G为1个阶数为n的极大外平面图,u为1个2度顶点且N(u)={v,w}。令X为1个顶点子集,
X={x∈V(G){u,v,w}|ε(x)=d(x,u)>d(x,ui)对于任意ui∈V(G){u}}。
若d(v)+d(w)=k,Xk={X|d(v)+d(w)=k}且f(k)=|Xk|,其中k≥9,则可以得到f(7)≥f(k-1)≥f(k)。
证明将用图形变换来证明。令图G为1个极大外平面图(见图6),xi1xi2(1≤i≤a)为1条弦或者为三角形△xi1vxi2(简写为△i)的1条边,其中a表示以v(而不是w)作为其中1个顶点的三角形的数目。可以看到当a≥2时,xi-1,2=xi1,i∈{2,3,4,…,a}是可能成立的。每一个三角形△i都对应着1个外边界为xi1xi2∪Qi的1个极大外平面图Gi,其中Qi是外边界上端点为xi1和xi2的1条路。G-{u,w}即Gi=G[V(Qi)],其中1≤i≤a。类似地,在G中有b个以w(而不是v)作为其中1个顶点的三角形,可以看出b≥0。用△yj1wyj2(简写为△′j)表示图G中边yj1yj2为弦的三角形。可以看出当b≥2时,yj-1,2=yj1,j∈{2,3,4,…,b}是可能的。每一个三角形△′j都对应着1个外边界为yj1yj2∪Q′j的极大外平面图G′j,其中Q′j为外边界上端点为yj1和yj2的1条路。即G′j=G[V(Q′j)]。当a=b=0时,对于任意1个顶点x∈V(G){v,w},vx∈E(G)和wx∈E(G)中至少有1个是成立的。用ki=|V(Qi)|-2≥1表示Qi(1≤i≤a)中既不与v相邻也不与w相邻的顶点数目,其中a≥1。类似地,当b≥1时,用lj=|V(Q′j)|-2≥1表示Q′j(1≤j≤b)中既不与v相邻也不与w相邻的顶点数目。设z0=N0(v)-N0(w),其中N0(v)=N(v)-{u},N0(w)=N(w)-{u}。由于v和w的对称性,下面仅证明三角形△xi1vxi2(其中1≤i≤a)的这种情况。
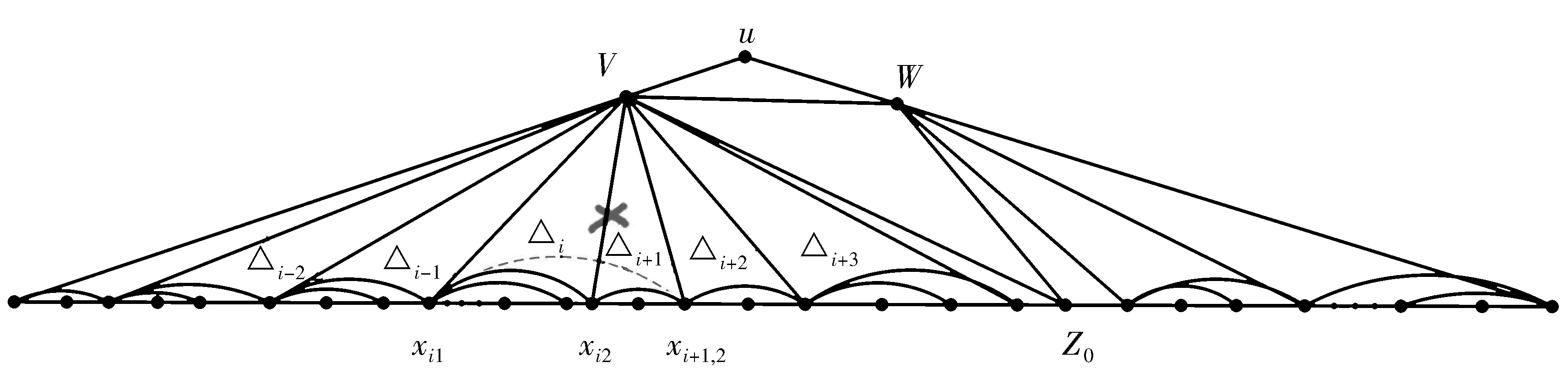
图6 变换ⅠFig.6 Transformation Ⅰ
变换Ⅰ假设在极大外平面图G中有2个三角形△xi1vxi2和△xi+1,1vxi+1,2(其中xi2=xi+1,1,i=2,3,4…,a)。令G′=G-vxi2+xi1xi+1,2(见图6)为通过在G中删除边vxi2再添加边xi1xi+1,2后得到的图,则G′也是1个阶数为n的极大外平面图。若在G中d(v)+d(w)=k,则dG′(v)+dG′(w)=k-1。接着证明当k≥9时,f(k-1)≥f(k)。下面分别比较G和G′中u和其他顶点的距离。
设Ai={ai∈V(Gi)|d(ai,xi1)≤d(ai,xi2)},Bi={bi∈V(Gi)|d(bi,xi1)>d(bi,xi2)},
X(Ai)={x∈Ai|x∈X},X(Bi)={x∈Bi|x∈X}。
若ai∈Ai,则dG′(ai,u)=dG(ai,u),dG′(ai,bi+1)=dG(ai,bi+1)-1,其中,bi+1∈Bi+1;dG′(ai,ai+2)=dG(ai,ai+2)-1。对于vi∈V(G){u,bi+1,ai+2},有dG′(ai,vi)=dG(ai,vi)。若在G中存在点ai0∈X,则在G′中一定有ai0∈X。若在G中ai0∉X,则在G′中可能有ai0∈X。综上可以得到|X(Ai)G′|≥|X(Ai)G|。
若bi∈Bi,则dG′(bi,u)=dG(bi,u)+1,dG′(bi,bi+l)=dG(bi,bi+l)+1,其中,l≥3;dG′(bi,ai+m)=dG(bi,ai+m)+1,其中m≥4;dG′(bi,bi-l′)=dG(bi,bi-l′)+1,其中,l′≥3;
dG′(bi,ai-m′)=dG(bi,ai-m′)+1,其中m′≥2。对于
vi∈V(G){u,bi+l(l≥3),ai+m(m≥4),bi-l′(l′≥3),ai-m′(m′≥2)},
有dG′(ai,vi)=dG(ai,vi)。所以,|X(Bi)G′|≥|X(Bi)G|。
根据Ai和Bi+1,Bi和Ai+1的对称性,有|X(Bi+1)G′|≥|X(Bi+1)G|,|X(Ai+1)G′|≥|X(Ai+1)G|。
若ai+2∈Ai+2,则dG′(ai+2,u)=dG(ai+2,u),dG′(ai+2,ai)=dG(ai+2,ai)-1,dG′(ai+2,bi-1)=dG(ai+2,bi-1)-1。对于vi∈V(G){u,ai,bi-1},有
dG′(ai+2,vi)=dG(ai+2,vi)。
所以,|X(Ai+2)G′|≥|X(Ai+2)G|。
根据Ai+2和Bi-1的对称性,有|X(Bi-1)G′|≥|X(Bi-1)G|。
若bi+2∈Bi+2,则dG′(bi+2,u)=dG(bi+2,u)。对于vi∈V(G){u},有
dG′(bi+2,vi)=dG(bi+2,vi)。
所以,|X(Bi+2)G′|=|X(Bi+2)G|。
同理可得
|X(Ai-1)G′|=|X(Ai-1)G|,|X(Bi-2)G′|=|X(Bi-2)G|,|X(Ai+3)G′|=|X(Ai+3)G|。
若bi+3∈Bi+3,则
dG′(bi+3,u)=dG(bi+3,u);dG′(bi+3,bi)=dG(bi+3,bi)+1;
dG′(bi+3,ai+1)=dG(bi+3,ai+1)+1;对于vi∈V(G){u,bi,ai+1},可以得到
dG′(bi+3,vi)=dG(bi+3,vi)。
注意dG(bi+3,bi)=dG(bi+3,vi)+dG(v,bi),dG(bi+3,u)=dG(bi+3,v)+1,其中,dG(v,bi)≥1,有dG(bi+3,bi)≥dG(bi+3,u),所以,在G中,bi+3∉X。可以得到dG′(bi+3,bi)=dG(bi+3,bi)+1>dG′(bi+3,u);在G′中,bi+3∉X。同理,有dG(bi+3,ai+1)≥dG(bi+3,u),dG′(bi+3,ai+1)>dG′(bi+3,u)。综上可知,|X(Bi+3)G′|=|X(Bi+3)G|。
根据Ai-2和Bi+3的对称性,有|X(Ai-2)G′|=|X(Ai-2)G|。
若ci+l∈Gi+l,其中l≥4,则dG′(ci+l,u)=dG(ci+l,u);dG′(ci+l,bi)=dG(ci+l,bi)+1;dG′(ci+l,ai+1)=dG(ci+l,ai+1)+1。对于vi∈V(G){u,bi,ai+1},有
dG′(ci+l,vi)=dG(ci+l,vi)。
注意dG(ci+l,bi)≥dG(ci+l,u),dG′(ci+l,bi)>dG′(ci+l,u);dG(ci+l,ai+1)≥dG(ci+l,u),dG′(ci+l,ai+1)>dG′(ci+l,u)。
所以,可得|X(Gi+l)G′|=|X(Gi+l)G|。
根据Gi-l′和Gi+l的对称性,其中l′≥3,有|X(Gi-l′)G′|=|X(Gi-l′)G|。
综上,可以得到|XG′|≥|XG|,即f(k-1)≥f(k),其中,k≥9。
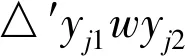
变换Ⅱ令Gn=Gn-1-vz0-wz0+x11x12+vx12(见图7)为通过在Gn-1中删除边vz0,wz0然后添加边x11x12,vx12后所得到的图。则Gn为1个极大外平面图,且d(v)+d(w)=7。令

图7 变换Ⅱ中的图Gn-1,GnFig.7 GraphGn-1,Gnof Transformation Ⅱ
A1={a1∈V(G1)|d(a1,x11)≤d(a1,z0)},B1={b1∈V(G1)|d(b1,x11)>d(b1,z0)}
A2={a2∈V(G2)|d(a2,z0)≤d(a2,x12)},B2={b2∈V(G2)|d(b2,z0)>d(b2,x12)}
现在比较Gn-1和Gn中点u和其他点的距离。
若a1∈A1,则dGn(a1,u)=dGn-1(a1,u);dGn(a1,b2)=dGn-1(a1,b2)-1。
对于vi∈V(G){u,b2},有dGn(a1,vi)=dGn-1(a1,vi)。所以,可以得到
|X(A1)Gn|≥|X(A1)Gn-1|。
根据B2和A1的对称性,有|X(B2)Gn|≥|X(B2)Gn-1|。
若b1∈B1,则
dGn(b1,u)=dGn-1(b1,u)+1;dGn(b1,v)=dGn-1(b1,v)+1;dGn(b1,w)=dGn-1(b1,w)+1。
对于vi∈V(G){u,v,w},有dGn(b1,vi)=dGn-1(b1,vi)。所以,可以得
|X(B1)Gn|≥|X(B1)Gn-1|。
根据B1和A2的对称性,有|X(A2)Gn|≥|X(A2)Gn-1|
综上,可以得到|XGn|≥|XGn-1|,且|XGn|≥|XGn-1|≥|XG|,其中在Gn中有d(v)+d(w)=7,则f(7)≥f(k-1)≥f(k),其中k≥9。引理5得证。
定理2令G为顶点数n≥6的1个极大外平面图,则
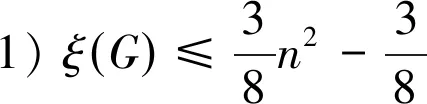

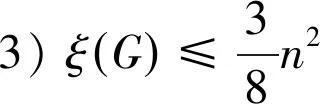
证明(1)首先考虑n为奇数的情况。
若n=7,则H7={H″1,H″2,H″3,H″4}(见图2),根据直接计算,可以得到
ξ(H″1)=13,ξ(H″2)=17,ξ(H″3)=16,ξ(H″4)=18。
所以,当n=7时结论成立。
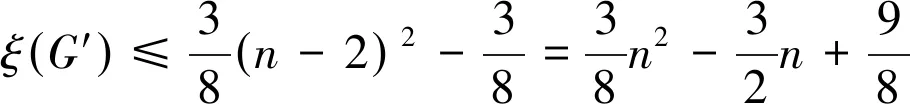

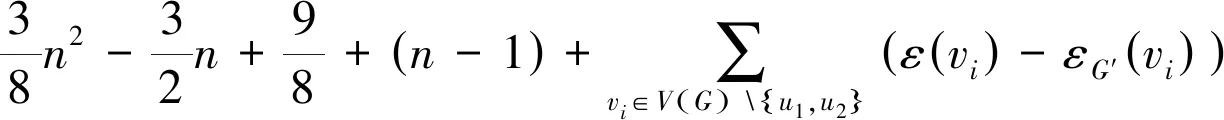
令V1={v∈V(G){u1,u2}|ε(v)=d(v,u1)>d(v,u)或ε(v)=d(v,u2)>d(v,u),u∈V(G){u1,u2}}则对于vi∈V1,有ε(vi)-εG′(vi)=1。对于vi∉V1,有ε(vi)=εG′(vi)。因此可得
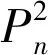
综上,当n=2k+1时,有

(2)若n=6,则H6={H′1,H′2,H′3}(见图1),根据直接的计算,可以得到结论成立。接着证明对于n≥10也成立,假设结论对于所有阶数小于n的极大外平面图都是成立的。令G为1个极大外平面图且|V(G)|=n,则一定存在1个顶点u且d(u)=2,N(u)={v,w}。设G′=G-u,则G′为1个极大外平面图且|V(G′)|=n-1,其中n-1≡1(mod 4)。
(1)
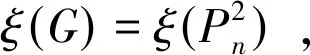

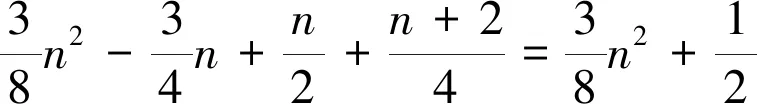
(3)若n=8,则H8={H‴i}(i=1,2,…,12)(见图3),根据计算,有
ξ(H‴1)=17,ξ(H‴2)=20,ξ(H‴3)=19,ξ(H‴4)=19,ξ(H‴5)=20,ξ(H‴6)=20,
ξ(H‴7)=20,ξ(H‴8)=21,ξ(H‴9)=20,ξ(H‴10)=24,ξ(H‴11)=21,ξ(H‴12)=24。
结论对于n=8成立。
接着证明对于n≥12结论也是成立的。假设结论对于阶数小于n的所有极大外平面图都是成立的。设G为极大外平面图且|V(G)|=n,则一定存在1个顶点u且d(u)=2,N(u)={v,w}。设G′=G-u,则G′为1个极大外平面图且|V(G′)|=n-1,其中n-1≡3(mod 4)。
(2)

则

综上可知,可知定理2得证。
