测量系统相频特性对动态测量误差影响研究

杨晓西，李正兴，陈一悰，梁 潘，汤晓君，曾翔君，刘懿莹

(1.国网陕西电力科学研究院，陕西 西安 710054；2.西安交通大学电气工程学院，陕西 西安 710049)

0 引言

测量不确定度作为对测量结果质量的定量表征，其意义已被广泛承认和接受，并日益受到重视。随着科学技术的日渐发展，动态测量已成为测试技术发展的必然趋势，是现代测试技术的主流，在现代测试技术中日渐处于主导地位。由于动态测量过程处于不断的运动变化状态，导致动态测量系统与静态测量系统相比，动态测量系统的不确定度来源和量值特性更多、更复杂。原有的与静态测量过程相关的不确定度评定方法已不能形成合理表征动态测量结果质量的指标，亟需开展与动态测量过程相关的动态测量不确定度原理与评定方法研究，以最终形成合理表征动态测量结果质量的量化指标——动态测量不确定度。

我国现行的《GB/T 27418-2017 测量不确定度评定和表示》(guide to the evaluation and expression of uncertainty in measurement 2017，GUM2017)[1]是在国际标准化组织(International organization for standardization,ISO)等七个国际组织于1993年公布的GUM1995等标准的基础上修订而来的。GUM2017的修订，标志着静态测量不确定度的评定和表示方法已趋于成熟。而动态测量不确定度的研究，由于其内容涉及面广泛、复杂，还处于初始阶段。目前，普遍存在以静态测量不确定度原理来评定动态测量不确定度的现象。将现有不确定度评定指南中提出的理论和方法扩展到包含动态测量不确定度的评定，已为国际学术界所共识。为了改变“以静代动”的不合理局面，并使静态与动态不确定度评定取得一致，需深入开展动态测量不确定度的研究[2]。

1 动态测量不确定度评定研究现状

按照国际计量局及国际标准组织(internation organization for standardization,ISO)等国际组织联合制定的《国际通用计量学基本名词》中的定义，动态测量的概念可表示为“量的瞬时值以及它随时间而变化量的值的确定”[3]。动态测量的概念是在19世纪80年代提出的。随着科学技术和测量技术的进一步发展，动态测量技术也越来越受到人们的重视。但国内外对动态测量的研究相对较少。

在动态不确定评估方面，有以下研究成果。林洪桦[4]提出动态测量中被测量的时变性、随机性和相关性，且测量系统本身也具有动态性的特征。同时，给出了通过建立动态测量数学模型、分解测量结果数学成分，进而根据测量结果所含的确定性和随机性成分分析评定动态测量不确定度，即动态测量不确定度的A类评定方法。徐陇云[5]提出，计算和合成动态测量标准不确定度的基本方法，仍是概率论、数理统计和随机过程理论中的计算随机变量(对于动态量是随机函数)及其函数数字特征的方法，主要是确定随机函数标准差以及由自变量的标准差求函数标准差的方法。罗云[3]提出动态测量不确定度基于先验知识分析：假设测量值概率分布类型的B类评定方法，并将动态测量不确定度的A类评定结果与B类评定结果进行合成，得到动态标准不确定度。但其合成结果的准确度有待进一步研究与讨论。张娟[6]分别对现有的动态不确定度常用研究方法(灰色系统理论评定、测量不确定度的贝叶斯评定、测量不确定度的蒙特卡罗方法评定)进行了阐述和评价；但其研究内容缺乏实例化验证，准确性有待考量。

在动态测量不确定度评定方法的具体应用方面，有以下研究成果：荆学东、黄韡霖等[7]提出了基于频率特性的传感器动态不确定度评定，给出一种基于测量信号频谱分析、运用动态不确定度的B类评定方法进行动态不确定度评定的方案。其数据分析与计算具有一定的可行性与合理性，但对动态特性的理解仍然较为局限，有待深入讨论。荆学东等[8]在其另一文章中提出一种基于动态测量系统结构组成及不确定度来源分析的动态测量不确定度评估，按照测量系统的结构组成，分析各个组分引入的不确定度分量，并最终进行标准动态不确定度合成。该方法具有一定的精度及可靠性，对于传感器测量系统可以进行一定修改后使用；但其同样由于对测量系统和测量过程的动态性理解较为局限，仍需讨论这一方法在更加广泛的动态测量中的实用性。Jaka Ogorevc采用蒙特卡罗法估计了体温计的动态测量不确定度[9]。E.Garcia采用贝叶斯滤波器改善动态坐标测量的不确定度[10]。S Holder通过改进Richardson-Lucy图像修复技术，修复光学精密坐标计量的动态测量不确定度[11]。

对已有研究成果进行分析，在现代不确定度评定方法及其应用研究方面，大多数文献主要介绍基于具体测量系统的不确定度评定方法，并未形成具有普遍指导意义的现代不确定度评定方法体系。很多研究成果提出了采用动态数据建模方法对动态随机过程进行预测，着重研究各种动态数据分析方法，但并没有深入研究动态不确定度的评定和预测模型。少数研究成果虽然提到对现代不确定度评定方法的研究，但仅仅是理论层面的分析，缺乏一定的实例支撑，且忽略了现代不确定度评定方法的应用研究。赵志刚[12]在其研究中提出，当前对于动态不确定度研究的主要问题在于：①理论体系不完备；②多维测量结果处理方法待完善；③缺乏数值处理的实用化方法；④实用化困难。

从动态不确定度评定的角度来看，需要尽可能准确地确定测量系统动态不确定度的来源。从构建测量系统的角度来看，应尽可能减小各动态测量误差来源。本文以二阶系统为例，通过仿真分析，讨论了测量系统的非线性相位对动态测量误差的贡献。该研究对构建动态测量系统，以及动态测量不确定度评定具有一定的意义。

2 测量系统结构与模型

2.1 测量系统结构

不失一般性地，本文以单输入单输出系统为例开展研究。目前的测量系统，大多是数字化测量系统。数字化测量系统结构如图1所示。其中，传感器感知一个或多个被测量后输出的信号，经过调理电路调理后，转换成便于采集卡采集的信号。调理电路具备信号放大、滤波、补偿等功能。该信号经采集后变成数字信号，再经过微处理器进行数字滤波、非线性校正、补偿等处理，获得与被测量接近的量值。

图1 数字化测量系统结构图

Fig.1 Structure of digital measurement system

传感器的非线性卷积结构及逆向结构如图2所示。

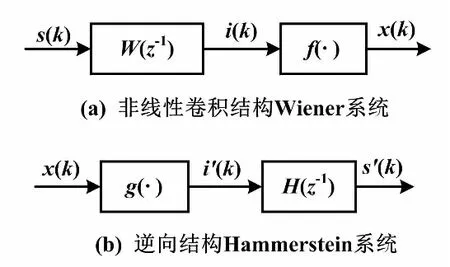
图2 非线性卷积结构及逆向结构示意图

如果对整个测量系统数字化，图1中传感器和调理电路部分，以及微处理器中的数字滤波部分，可以等效为如图2(a)所示的Wiener系统。图2中：W(z-1)为滤波系统；f(·)为非线性映射函数。如果要实时获得准确的被测结果，理论上应在微处理器中构建如图2(b)所示的Hammerstein系统，且使得g(·)=f-1(·)、H(z-1)W(z-1)=I。显然，这两个条件是很难满足的。

首先，通常只能有g(·)≈f-1(·)，使得测量系统中存在非线性误差等静态测量误差。当然，一定范围的非线性误差是可以接受的。其次，由于W(z-1)往往是低通滤波器特性，要使得H(z-1) ·W(z-1)=I，H(z-1)必须是W(z-1)的逆。要满足上述条件，则H(z-1)往往必须具有高阶差分器的特性。由于高阶差分器受噪声影响很严重，实用过程中几乎无法实现；而缺失H(z-1)则会使得在线测量结果产生很大的随机误差。因此，实际获得测量系统特性只能是尽可能逼近I。于是，测量结果中就存在时间滞后。当然，对于大多数的在线测量，测得值在一定范围内滞后于被测量的时间，也是可以接受的。因此，实际测量系统的Hammerstein系统中，往往只有g(·)，没有H(z-1)；只有在需要带宽补偿的时候，才会增加含有少量差分项的H(z-1)。

由此可知，对于测量结果：一方面，允许存在一定的静态误差；另一方面，少许的时间滞后是可以接受的。

2.2 测量系统的模型

由2.1节可知，测量系统包含两部分：一部分是静态特性模型，另一部分是动态特性模型。静态模型存在静态误差。如果不考虑静态误差，测量系统的动态传递函数可以等效为低通滤波器。对于有的测量系统而言，其主要动态特性呈现为一阶低通滤波器，例如热电偶测温系统。有的测量系统呈现二阶低通滤波器特性，如谐振子加速度测量系统。还有的测量系统具有高阶低通滤波器动态特性，其往往可以用二阶低通特性来近似。为研究系统相位对动态测量误差的影响，本文暂不考虑静态特性误差。不失一般性，本文采用如式(1)所示的二阶低通滤波器，近似测量系统的动态特性传递函数。

(1)

式中：ωn为二阶系统自然震荡角频率；ζ为系统阻尼比。

3 相频特性对动态测量误差的影响

对于如式(1)所示的二阶系统，令ωn=100 rad/s、ζ分别为0.707和0.4。根据这两种情况，分别讨论相频特性对动态测量误差的影响。前者代表线性相位系统，后者代表非线性相位系统。二阶系统频率特性Bode图如图3所示。

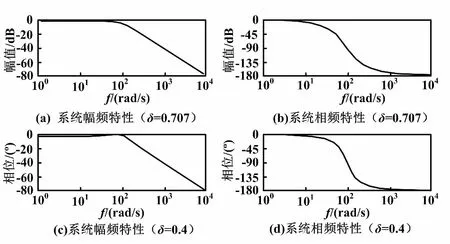
图3 二阶系统频率特性Bode图

从图3中的幅频特性可以看到：当ζ=0.707时，低频时增益基本为1，到接近通带截止频率处时，逐渐减小；当ζ=0.4时，低频时增益基本为1，到接近通带截止频率处时，先增大再逐渐减小，且在小于通带截止频率附近形成一个凸峰。输入信号分别为三个正弦波信号，其幅值均为1，频率分别为12.57 rad/s、75.40 rad/s、125.66 rad/s。这三个信号分别代表远离通带截止频率的低频率分量、临近通带截止频率的信号分离，以及远离通带截止频率的高频分量。第四个输入信号为这三个频率分量正弦波合成的混合信号。

3.1 线性相位系统

当ζ=0.707时，不同输入信号的二阶系统响应如图4所示。

三个不同频率正弦波信号在通过线性相位测量系统后得到的响应曲线分别如图4(a)～图4(c)所示。其分别产生相位滞后0.18 rad、1.19 rad、1.89 rad。其对应信号频率的时延分别为14.2 ms、15.7 ms、15.0 ms，基本相同。这表明系统引入的相位差与输入信号的频率基本满足线性关系。

各频率分量幅值分别为0.999 9、0.869 5和0.535 1。随着频率的增大，三个响应均有不同程度的衰减。这一衰减是由于线性相位二阶系统幅频特性的衰减引起的。如果直接比对各图中不同时刻的输入与输出值之差，最大偏差值则分别约为δ1=0.18、δ2=1.05、δ3=1.27。由此可见，随着频率的增大，同一时刻输入输出之间的偏差大于幅值的衰减。这一增加的偏差，是由于相频特性引入的。如果对每个频率的响应信号均平移其对应的滞后时间，则可消除相频特性引入的附加偏差。

由上述三个频率正弦波组合的复合信号的响应如图4(d)所示。由图4(d)可见，复合信号的幅值约为2.8、响应的幅值约为2.2，两者同一时刻的差值最大约为2.486。若对响应信号平移0.15 ms，得到如图5所示的线性相位测量系统的三频率合成信号响应曲线。其输入与响应信号的最大差值约为0.6。由于三个频率分量的幅值衰减分别为-0.000 1、-0.130 5和-0.464 9，三者之和为-0.595 5。因此，该差值主要来源于幅频特性，相频特性基本没有贡献。

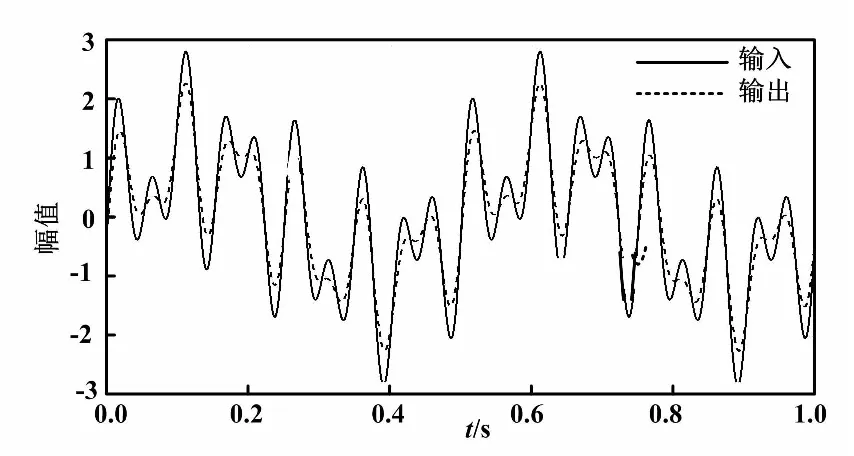
图5 三频率合成信号响应曲线

3.2 非线性相位系统

三个不同频率正弦波信号在通过非线性相位测量系统后得到的响应曲线，分别如图6(a)～图6(c)所示，分别产生约0.1 rad、0.95 rad、2.09 rad的相位滞后，对应信号频率的时延分别为8.1 ms、12.6 ms、16.7 ms。时延随着频率的增大而逐步增大。各频率分量幅值分别为1.010 8、1.348 4和0.861 9，随着频率的增大先增大后减小。这一变化是由于非线性相位二阶系统幅频特性引起的，小于带宽截止频率附近的频率段存在凸峰。如果直接比对图6中不同时刻的输入与输出值之差，最大偏差值则分别约为δ1=0.1、δ2=1.12、δ3=1.61。由此可见，和线性相位系统一样，随着频率的增大，同一时刻响应与输入之间的偏差比幅值的衰减还要大。这一增加的偏差，也是由于相频特性引入的。如果对每个频率的响应信号均平移其对应的滞后时间，同样可消除相频特性引入的附加偏差。

当ζ=0.4时，不同输入信号的二阶系统响应曲线如图6所示。

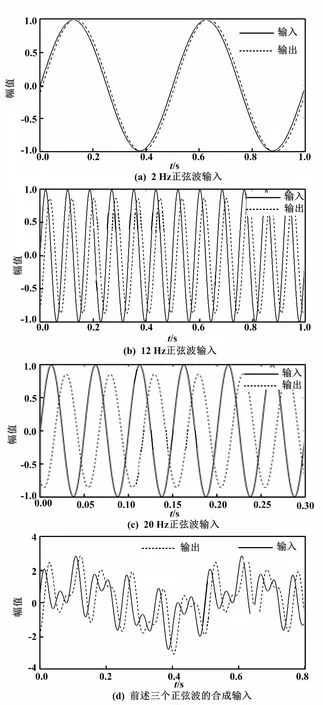
图6 不同输入信号的二阶系统响应曲线(ζ=0.4)

由上述三个频率正弦波组合的复合信号响应如图6(d)所示。由图6(d)可见，复合信号的幅值约为2.78、响应的幅值约为3.15，两者同一时刻的差值最大约为2.63。

非线性相位测量系统对合成信号响应曲线对比如图7所示。

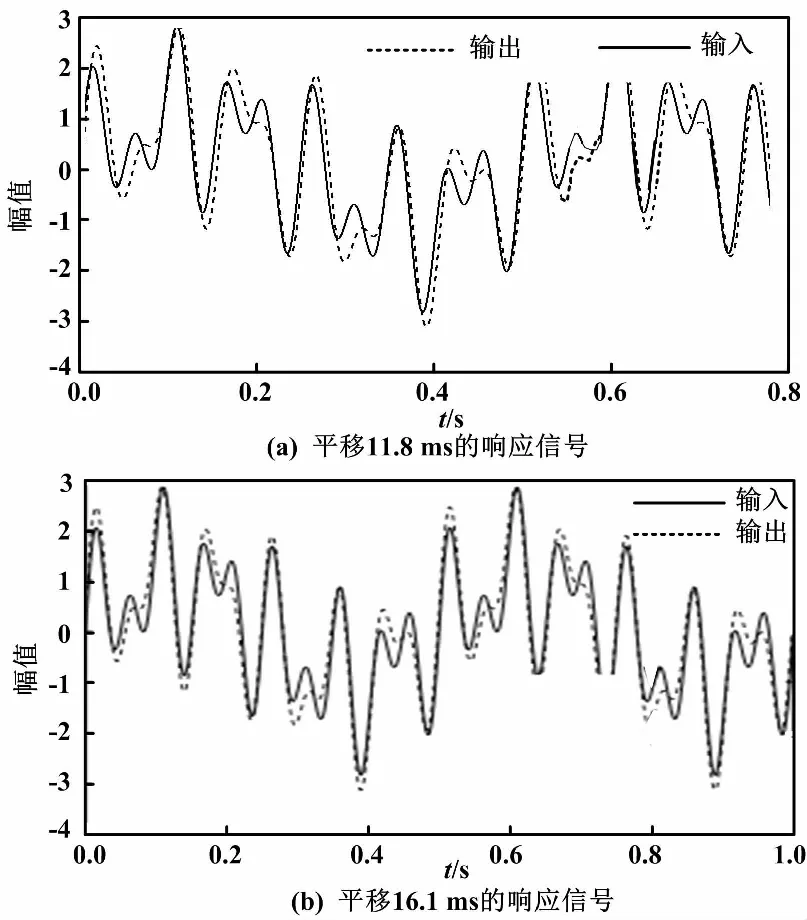
图7 非线性相位测量系统对合成信号输入与平移后的响应对比图

如果对图6(d)中的响应信号分别平移11.8 ms，即三个分量滞后时间的均值，得到图7(a)。按照相关运算，使得响应信号与输入信号的偏差能量最小，可计算得到滞后时间16.1 ms。将图6(d)中的响应信号分别平移16.1 ms，得到图7(b)。从图7可以看出，平移11.8 ms后的最大偏差约为0.94，平移16.1 ms后的最大偏差约为0.66。明显可知，响应平移采用偏差能量最小化求得的时间，最大偏差能大幅减小。实际上，当ζ=0.4时，三个频率分量的幅值偏差分别为0.010 8、0.348 4和-0.138 1，三者之和为0.221 1，明显小于0.66。因此，即使采用偏差能量最小化法求平移时间，得到的偏差也远大于分量幅值的偏差。这个偏差主要来自于非线性相位。

为便于比较两个二阶系统响应与输入之间的偏差，将参数列出。不同测量系统响应幅值变化及偏差如表1所示。

表1 不同测量系统响应幅值变化及偏差

从表1中可以看出，线性相位系统的低频响应幅值变化小于非线性系统，而过渡带的信号响应与三个频率符合信号的响应则相反。在同一时刻响应与输入信号的偏差方面，尽管ζ= 0.4时增益偏差大，但ζ=0.707的低频响应偏差大于ζ=0.4时的偏差。其主要原因在于ζ=0.707时响应的滞后时间比ζ= 0.4时的更长。随着频率的增大，尽管ζ= 0.4时增益偏差比ζ= 0.707时的小，但对应的偏差反而增大了。其主要原因在于此时的相位滞后比ζ= 0.707时大。由此可得出结论，同时刻响应与输入的偏差，主要受相位影响。

3.3 响应平移比对分析

3.1小节和3.2小节比对了ζ=0.707和ζ=0.4时二阶系统响应的幅值变化，以及同时刻响应与输入之间的偏差。实际上，对于许多测量系统，用户更关心的是对输入信号的完整复现，滞后一定范围内时间是可以接受的，同一时刻响应与输入的偏差也并不重要。例如，通电话的过程中，需要更关注的是语音的清晰度，对方的回答滞后些许时间也是可以接受的。再如电能计量，往往并不需要即刻得到测量结果，而是更希望得到准确的结果。这就要求能准确复现被测信号的波形。这也是实际测量系统的Hammerstein系统中，往往只有g(·)而没有H(z-1)，却也一直应用广泛且性能良好的原因。

从3.1节和3.2节的分析可知，为了便于量化动态测量的误差，响应的平移是必须的。对于线性相位系统，平移时间比较好确定，因为各分量的滞后时间基本相等，给定系统的传递函数，可直接求得滞后时间。而对于非线性相位，由于测量信号的输入是未知的，难以根据响应与输入的偏差能量最小化来求得最佳滞后时间。因此，其响应的最大偏差也难以计算。

根据表1中两类测量系统对复合频率信号的测量结果，若采用平移后的测量结果进行对比，则对于线性相位系统，测量过程中产生的动态测量误差基本取决于其幅频特性。对于非线性相位系统，测量过程中产生的动态误差同时受到系统幅频特性、相频特性的影响。对于具有非线性相位特性的测量系统，评定其测量过程中产生的误差这一工作将更加复杂。

对于上述线性相位系统，被测信号中含有的20 Hz信号已经位于其通频带外。观察测量结果可知，对应的响应已产生较大的幅值衰减。而对于非线性相位系统，其带宽范围更大，20 Hz信号位于其测量带宽内。由于被测信号均位于满足带宽要求，此时非线性相位测量系统应当具有较小的动态误差，才能保证测量结果的准确性。但观察时移后的动态测量信号可知，两类系统的动态测量最大偏差也是相当的。非线性相位测量系统在测量频率位于其带宽内的信号时，测量结果仍具有不可忽视的动态误差。这进一步说明，非线性相位是动态测量过程中的重要误差源。

虽然本文假定三个分量的幅值相等，而多数被测信号的频谱随着频率增大而幅值减小，但是在电力系统，尤其是电力系统的暂态分析中，并非如此。例如放电，高频电流分量可能比低频分量电流更大。因此，在测量过程中，为了获得更好的动态测量结果，应当尽可能使得测量系统具有线性相位的特性，避免非线性相位特性。

4 结论

本文采用二阶系统模拟测量系统，通过三个不同频率的单频信号以及其混合信号，分别对线性相位系统和非线性相位系统进行激励，并通过仿真分析对比了其响应。对比结果表明，非线性相位测量系统在测量频率位于其带宽内的信号时，测量结果具有显著的动态误差，非线性相位是动态测量不确定度的一个重要来源。此外，按照输入与输出的偏差能量最小化原则平移信号，线性相位系统的响应对于输入的滞后时间是确定的；而非线性相位系统的响应的滞后时间并不确定，其与信号各频率分量有关。因此，为了减小动态测量误差，应该尽可能将在线测量系统设计成具有线性相位的系统。