集中供热系统热网流量的优化神经网络控制
2020-07-06薛贵军
顾 伟,薛贵军
(华北理工大学电气工程学院,河北 唐山 063210)
0 引言
热网中对温度、流量的控制,是集中供热系统一次网和二次网在发生热传递时的关键环节,直接关系到整个供热系统的热量分配和温度调节[1]。由于集中供热系统本身存在的非线性、时滞性、强耦合等特点,再加上控制系统工作效率的低下和不精确,往往使得供热系统不能及时、准确地满足热用户对温度的需求[2]。而换热站一次网和二次网进行热传导时,温度和流量的控制没有达到最优,会使得热量在传导至热用户的过程中分布不均匀,并且不能尽可能地覆盖整个供热网络。这将导致热用户的室内温度不达标的问题,并造成资源的浪费[3]。
以往对换热站的控制都是采用传统的比例积分微分(proportional-integral-differentive,PID)控制器进行操作,精度较低,效果也差强人意。近几年,虽然神经网络算法逐渐成熟,但在集中供热领域应用仍较少。文献[4]提出了一种专家系统优化后的模糊PID控制器,虽然优化了量化因子,但由于专家系统本身可移植性差、解决问题能力弱,不适合推广使用。文献[5]提出一种自适应模糊控制器解决多变量耦合的问题,能够提高未知条件下系统的稳定性,但不具有普适性。文献[6]采用径向基函数(radial basis function,RBF)神经网络优化PID控制器,提高了控制器的收敛速度的精度,但容易早熟。文献[7]提出一种多变量自适应解耦PID控制器,但该PID控制器抗干扰能力差,不适用于非线性系统。
采用改进的粒子群优化(particle swarm optimizition,PSO)算法反向传播(back proporgation,BP)神经元的权值,得到PID控制器中新的kp、ki、kd,对换热站的流量进行优化控制。该方法可解决供热系统难以进行精确系统建模的不足,提高系统的控制精度并减少能耗,具有较强的通用性。
1 优化神经网络PID控制器
1.1 集中供热系统结构原理
集中供热系统主要由一次网、二次网和换热站三个部分组成。热源产生的热量由一次网传递到换热站,再由换热站将热量传递给二次网,最终传送到各个热用户家中。一次网的循环水返回热源重新加热后,二次网的循环水将热量传递到热用户,再重新返回换热站吸收热量[8]。
1.2 BP神经网络
BP神经网络结构如图1所示。

图1 BP神经网络结构图
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,工作信号始终正向流动,没有反馈结构。在训练网络权值的过程中,数据沿着减少误差的方向传播。绝大多数人工神经网络都采用这种网络及其变化形式。BP神经网络由输入层、隐含层和输出层组成。在保证网络性能和泛化能力的前提下,确定隐含层层数的基本原则是:在满足精度的前提下,尽可能选取更紧凑的网络结构[9]。输入层负责接收外部的输入信息。外部输入变量的多少决定了输入节点的个数。对于BP神经网络PID控制器,输出层输出的参数就是PID控制器中的kp、ki、kd这三个控制参数。试验采用3-4-3三层BP神经网络,对kp、ki、kd进行优化。j列有三个输入,分别为输入r(k)、上一时刻输出y(k-1)、上一时刻误差信号e(k-1)。i列为隐含层神经元。l列为kp、ki、kd三个输出参数。
1.3 PSO算法
PSO算法是一种基于随机全局迭代的进化算法,具有速度快、运算较容易、易于实现、参数调整量小等优点。PSO算法对一群随机粒子进行初始化,结合不同的目标函数,为每个粒子分配各自的适应度值。在PSO迭代的过程中,粒子利用个体极值P(best)和全局极值g(best)调整并更新粒子本身的速度和位置,并搜索当前最优粒子。经过反复迭代计算后,可以找到待寻优函数的最优解集[10]。自适应粒子群算法公式如下。
假设在一个D维的搜索空间内有n个粒子,每个粒子的速度根据式(1)来计算。
V(k+1)id=ωVkid+c1r1(Pkid-Xkid)+
c2r2(gkid-Xkid)
(1)
X(k+1)id=Xkid+V(k+1)id
(2)
式中:ω为权重系数通常取较大值,其数值由最优适应度值Q来决定;d=1,2,…,D;i=1,2,…,n;Vid为粒子速度;Pid为该粒子当前的最优位置;gid为整个粒子群当前所在的最优位置;k为当前迭代次数;c1、c2(非负常数)为加速度因子;r1和r2为[0,1]间的随机数。
一般情况下,粒子的速度和位置限制在区间[-Xmax,Xmax]、[-Vmax,Vmax]内,以防止粒子群迭代寻优过程中出现盲目搜索的情况。
两个变量之间存在如下关系:
(3)
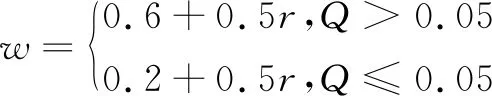
(4)
式中:g(t)为种群的最优适应值;r为均匀分布在[0,1]的随机值;Q为种群最优适应值的相对变化率;w与r成比例关系。
粒子群半径R是全局极值与种群内所有粒子之间空间距离的最大值,它与pgd和xid的关系如下:
(5)
(6)

在全局最优位置的粒子从第n代迭代到第(n+1)代的过程中,如果P(n+1) 适应度值优于上一代,则用P(n+1)的适应度值代替P(n)。反之,如P(n)的值保持不变,则算法会选取不同的参数进行下一次迭代,并一直运行,直至达到迭代上限次数。
ΔP=mΔPn+(1-m)gPn
(7)
P(n+1)=P(n)+ΔP(n+1)
(8)
1.4 PSO-BP-PID控制器结构
PID控制器由比例单元P、积分单元I和微分单元D三部分组成。通过对kp、ki、kd的设置,来实现对系统的控制[11]。但是常规的PID控制器主要适用于线性和动态特性不随时间变化的系统。对于供热系统这种具有时滞性、非线性、强耦合等特点的非线性系统,则需要对常规PID控制器进行改进。BP神经网络具有能逼近任意非线性,自身函数结构和算法简单、明确的特点。因此,基于BP神经网络的PID控制器可以通过网络自身的学习,找到某一最优控制规律下的kp、ki、kd参数。基于BP神经网络的PID控制器不仅兼备了PID算法和神经网络隐含元个数清晰的优点,还缩短了控制器的训练学习时间、加快了神经网络的收敛速度[12]。PSO-BP-PID控制器结构如图2所示。

图2 PSO-BP-PID控制器结构图
1.5 PSO-BP-PID神经网络控制模型
为了满足热用户对室内温度的要求,主要对管网内热媒的流量进行控制,即改变循环泵的工作频率,通过自适应粒子群算法得到优化后的神经网络初始权值。将其代入BP-PID控制器,可得最优控制规律下的kp、ki、kd参数。
基于BP神经网络的PID控制器不仅利用BP算法来训练PID神经元网络,还把PID神经网络和多变量被控对象整合为一个完整系统。BP网络的目标函数如下:
(9)
式中:n为采样个数;m为被控对象个数。
PSO-BP-PID控制模型如图3所示。

图3 PSO-BP-PID控制模型
由于BP算法应用性强,不需要具体的数学模型,能够对PID控制器的权值进行解耦和实时修改。但由于BP算法对计算过程太过依赖,容易导致停滞和早熟,且算法的局部寻优能力也需要提高。所以本文采用基于变异思想改进的粒子群算法,对BP神经网络参数进行优化。在PSO算法中加入变异程序,按照一定的概率再次初始化部分粒子,增加找到全局最优解的机率。这样可以实现提升结点位置向量变异及粒子群节点与BP-PID神经网络之间的相互映射效果。
2 试验仿真
2.1 试验参数设置
BP-PID控制器是一个三输入三输出的控制器,选取流量设定值r(k)、上一时刻的流量值y(k-1)和上一时刻误差信号e(k-1)为输入;BP-PID控制器的输出记作kp、ki、kd,用于控制热网内循环泵的频率,实现对系统管网内流量的控制。选取变异粒子群优化算法的种群规模M为50,训练次数为500次,ω为0.3~0.7,学习因子c1、c2为1.372 8,变化因子∝为0.69。
2.2 预测结果
流量输出对比如图4所示。

图4 流量输出对比图
图4中:输出1为解耦PID控制;输出2为模糊PID控制;输出3为PSO-BP-PID控制。从图4可以看出,PSO-BP-PID控制器通过神经网络的优化,实现权值系数的实时更新和调整,对供热系统的强耦合性也有一定的改善。相比于解耦PID和模糊PID的控制效果,PSO-BP-PID控制器的调节时间大幅缩短、动态性能得到改善、超调量减小,控制系统具有良好的稳定性。
3种控制算法的控制结果对比如表1所示。
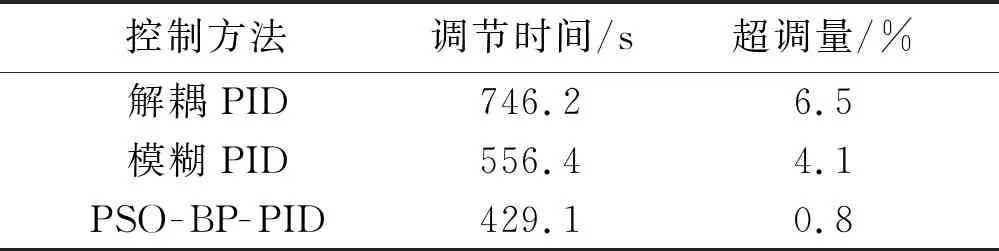
表1 控制结果对比
3 结论
本文设计了采用PSO算法优化的BP-PID控制
器,来优化对集中供热系统流量的控制。采用改进后的PSO算法来调整BP神经网络中的初始权值,得到新的kp、ki、kd。试验结果表明,本文提出的PSO-BP-PID控制器不仅能够改善供热系统的时滞性、强耦合等特点,还能增强系统的控制精度、缩短调节时间,提升系统的稳定性。该方法为集中供热系统的流量控制提供了较好的优化策略,具有广阔的应用前景。
