让几何思维水平“拔节”

赵一峰

摘要：荷兰学者范希尔夫妇将学生的几何思维水平分为五个层次。这五个层次的水平是不连续的，但却是顺次的。也就是说，学生在进入某一水平学习之前，必须掌握之前水平的大部分内容;或者说没有一种教学法能让学生跳过低的水平层次，而直接进入高的水平层次。据此，教学苏教版小学数学六年级上册《表面涂色的正方体》一课时，让学生通过观察对话明晰“前层次”，通过想象表征固化、丰盈已有层次，通过归纳运用提升、突破到下一层次。

关键词：几何思维水平 范希尔理论 《表面涂色的正方体》

荷兰学者范希尔夫妇经过理论和实践两方面的长期探索，指出学生的几何思维水平存在五个层次，分别为——层次0：直观（Visualization，即能通过整体轮廓辨认图形，并能操作其几何构图元素;能使用标准或者不标准的名称描述几何图形;但无法使用图形的特征或要素名称来分析图形，也无法对图形做概括的论述）;层次1：分析（Analysis，即能分析图形的组成要素及特征，并依此建立图形的特性，但无法解释特性之间的关系，也无法了解图形的定义;能根据组成要素比较两个图形，利用某一性质做图形的分类，但无法解释图形某些性质之间的关联，也无法导出公式和使用正式的定义）;层次2：非形式化演绎（Informal deduction，即能建立图形及图形性质之间的关系，提出非形式化的推论，了解构建图形的要素;能进一步探求图形的内在属性和其包含关系，使用公式与定义及发现的性质做推论;但不能由不熟悉的前提去证明结果的成立，也不能建立定理网络之间的内在关系）;层次3：形式化演绎（Formal deduction，即能了解到推理的重要性和“不定义元素”“公理”的意义，确信定理是需要形式逻辑推演才能建立的;能猜测并尝试用演绎方式证实猜测，能够以逻辑推理解释几何学中的定理等，从而建立定理间的关系网络）;层次4：严密性（Rigior，即能在不同的公理系统下严谨地建立定理，以分析比较不同的几何系统）。

这五个层次的水平是不连续的，但却是顺次的。也就是说，学生在进入某一水平学习之前，必须掌握之前水平的大部分内容;或者说没有一种教学法能让学生跳过低的水平层次，而直接进入高的水平层次。因而，教学小学数学“图形与几何”领域相关内容时，教师应了解学生所在的水平层次，明晰“前层次”，固化已有层次，并尽可能地让学生有所提升。据此，笔者在教学苏教版小学数学六年级上册《表面涂色的正方体》一课时，让学生通过观察对话明晰“前层次”，通过想象表征固化、丰盈已有层次，通过归纳运用提升、突破到下一层次。

一、在观察对话中明晰

到了六年级，仍会有少部分学生没有达到层次1，且大部分学生并没有明晰自己所处的层次。因此，在教学伊始，师生就学习对象进行对话——学生对所学对象做出观察，确定下一步的学习;教师了解学生是如何理解课题相关概念的。而观察和对话是一种学生主动参与、积极思考的知觉过程，能帮助学生打开思维之门。

【教学片段1】

师  （出示图1）这个表面涂色的大正方体，每条棱都平均分成2份，能切成多少个同样大的小正方体？你是怎么知道的？

生  8个。看一看，数一数就能知道了。

师  这里切成的每个小正方体的六个面是怎样涂色的？

生  每个小正方体都有3个面是涂色的。

（教师同步展示图2。）

师  （出示图3）这个大正方体的每条棱是怎样分的？能切成多少个小正方体？

生  平均分成3份，能切成27个小正方体。

师  切成的小正方体涂色的面有哪些情况？

生  有些小正方体是3个面涂色，有些是2个面涂色，有些是1个面涂色。

师  三面涂色、两面涂色、一面涂色的小正方体各有多少个？分别在什么位置呢？

（学生讨论后明确：三面涂色的小正方体有8个，位于大正方体的顶点处;两面涂色的小正方体有12个，位于大正方体棱的中间;一面涂色的小正方体有6个，位于大正方体面的中间。教师依次出示图4、图5、图6。）

师  你还想到了什么？

生  在大正方体的里面，有1个小正方体是没有涂色的。

师  你怎么想到的？

生  切开后共得到27个小正方体，但是将三面涂色、两面涂色、一面涂色的小正方体个数加起来，只有26个，所以还有1个。

生  有涂色面的小正方体都在大正方体的表面，在最里面应该还有1个小正方体，任何面都没有涂到颜色。

（教师同步展示图7。）

师（出示表1）为了方便比较，我们可以把刚才研究的结果记录在表格里。

这一环节，教师引导学生先观察每条棱平均分成2份的情况，再观察每条棱平均分成3份的情况，学生通过看一看、指一指、说一说、想一想等多种感官参与探究活动。接着，教师通过问题引领，使学生的数学思考层层深入，发现了涂色面的小正方体个数与其在大正方体上的位置之间的关系，为后续探究活动的顺利开展夯实基础。这样的教学，探寻到学生的几何思维水平既达到了层次0，如：“有些小正方体是3个面涂色，有些是2个面涂色，有些是1个面涂色”;也部分达到了层次1，如：“三面涂色的在顶点处;两面涂色的位于棱的中间;一面涂色的位于面的中间”“一共27个小正方体，除掉涂色的26个，应该还有1个没有涂色”。

二、在想象表征中丰盈

想象是指在仔细观察后，对头脑中已有空间表象加工、改造、结合，产生新表象的心理过程。教师要引导学生基于已有经验和最低程度的提示，明确概念的意义，表達自己对内在结构的看法，由此开始形成学习的关系系统。

【教学片段2】

师（出示图8、图9）这两幅图分别是把大正方体的每条棱平均分成4份和5份。请仔细观察，然后完善表格。

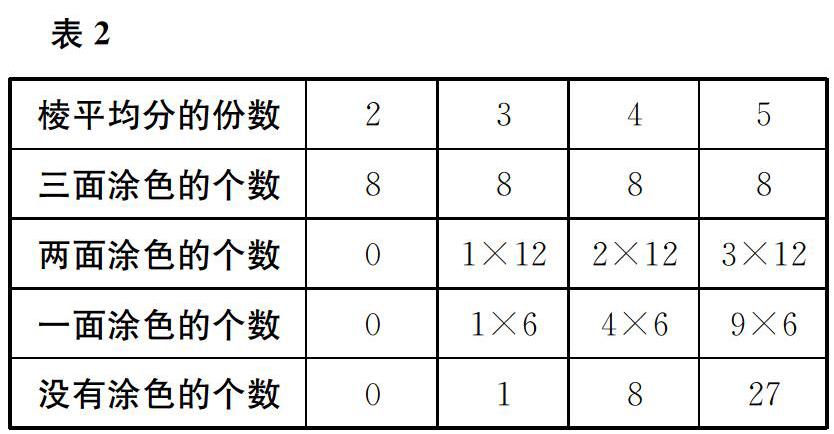
（学生观察、填表，得到表2。）

师  请同学们仔细观察图形及表格里的数据，你有什么发现？

生  三面涂色的都是8个，因为三面涂色的小正方体都在大正方体的顶点上。

生  两面涂色的小正方体都在大正方体的棱上。正方体有12条棱，把棱三等分时两面涂色的有1个12，四等分时两面涂色的有2个12，五等分时两面涂色的有3个12。

师  这里的“1”“2”“3”你是怎样理解的？它和棱被平均分的份数有什么关系？

生  每条棱两面涂色的个数比所分的份数少2。因为两端都是三面涂色的小正方体。

生  我发现，一面涂色的都在大正方体6个面的中间。每条棱平均分成3份的，一面涂色的个数是6×（3-2）2;每条棱平均分成4份的，一面涂色的个数是6×（4-2）2;每条棱平均分成5份的，一面涂色的个数是6×（5-2）2。

师  没有面涂色的小正方体的个数有没有规律呢？

生  （3-2）3，（4-2）3，（5-2）3。

师  照这样推算，你能得出把棱六等分时，三面涂色、两面涂色、一面涂色和没有面涂色的小正方体的个数吗？

生  三面涂色的小正方体有8个，两面涂色的小正方体有12×（6-2）个，一面涂色的小正方体有6×（6-2）2个，没有面涂色的小正方体有（6-2）3个。

这一环节，教师放手让学生边观察边想象，自主探究每条棱平均分成4份、5份的规律，类比迁移前面探究得到的规律;而探究棱六等分的规律时，直接让学生脱离直观图形，在头脑中“看”出结论。从而实现层次2——“非形式化演绎”，如：“三面涂色的在顶点处，两面涂色的在棱上，所以每条棱两面涂色的个数比所分的份数少2……”

三、在归纳运用中突破

教学的尾声，教师应引导学生运用不完全归纳提出一般化猜想，再用逻辑弥合其“猜”的过程，获得演绎经验，使他们对学习对象之间的关系越来越明确。当学生在学习活动中能对研究对象舍去无关紧要的内容，而只保留其中的数学关系，形成数学结构时，就已经触摸到了层次3——“形式化演绎”。

【教学片段3】

师通过刚才的研究，我们发现，三面涂色、两面涂色、一面涂色、没有面涂色的小正方体的所在位置和个数都是有规律的。如果把一个大正方体的棱平均分成n份，你能根据我们之前发现的规律，表示出三面涂色、两面涂色、一面涂色、没有面涂色的小正方体的个数吗？

生  三面涂色的小正方体有8个。

生  两面涂色的小正方体个数为12（n-2）。

师   n-2表示什么？

生  表示每条棱两面涂色的小正方体的个数。

生  一面涂色的小正方体个数为6（n-2）2。

师  （n-2）2表示什么？

生  表示每个面中间一面涂色的小正方体的个数。

生  没有面涂色的小正方体个数为（n-2）3。

……

学生通过上一阶段的非形式化演绎，能依据图示去指认两面涂色、一面涂色的小正方体的位置，但也深感随着棱分割的份数增加，看图并不是一个好的问题解决方式，应该通过推理得到结论。这样，n-2就自然而然成了这类问题的前提：“2”指的是每条棱靠近顶点的两个小正方体，因为这两个是三面涂色的，所以在计算两面涂色的个数时要减去。同理，计算一面涂色的个数时，要减去棱附近的小正方体，即（n-2）2。没有面涂色的个数亦如此。至此，12（n-2）、6（n-2）2、（n-2）3成为计算表面涂色的小正方体个数的工具性前提。

这样，当教师出示问题：“将一个表面涂色的长为6厘米、宽为5厘米、高为4厘米的大长方体，切成棱长为1厘米的小正方体，三面涂色、两面涂色、一面涂色、没有面涂色的小正方体个数各是多少？”学生的演绎思路随之被打开：类似地，长方体中，两面涂色的个数=[（a-2）+（b-2）+（c-2）]×4，一面涂色的个数=[（a-2）×（b-2）+（a-2）×（c-2）+（b-2）×（c-2）]×2，没有面涂色的个数=（a-2）×（b-2）×（c-2）……最后用6、5、4替换a、b、c，问题迎刃而解。

在以上归纳运用的过程中，学生头脑中的几何概念逐步脱离情境而独立存在。一旦知识形成了相互联系的网络，学生便理解了在不违背前提的情况下，所有的推论必然获得正确的答案。同时，学生还会回顾自己所用的方法并形成一种观点，对象和关系也被统一并内化进一个新的思维领域。

需要说明的是，几何思维水平发展是一个长期的过程，因此本节课主要展现了层次1到层次2的跨越（学生在之前的学习中已经达到了层次1;而层次3只是让学生初步触摸;层次4对于刚刚接受欧氏几何启蒙的小学生来说，无论知识储备，还是心理认知，都无法实现）。但我们仍然可以通过上述教学看出，这一理论是指导“图形与几何”领域教学的有力武器。

参考文献：

[1] 鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[2] 周淑红，王玉文.小学数学核心素养的特质与建构[J].数学教育学报，2017（3）.

[3] 孔凡哲，史宁中.中国学生发展的数学核心素养概念界定及養成途径[J].教育科学研究，2017（6）.