基于多目标规划的超市鲜奶库存决策研究

摘要：本文对超市“巴氏杀菌奶”的库存策略进行研究，建立多品种新鲜牛奶下的多目标规划的一般模型。以广州市某连锁超市为例，建立多目标规划的决策模型，并利用winQSB20进行求解，求解结果可以有效实现超市的多个目标。

关键词：巴氏杀菌奶;多目标规划;决策模型

中图分类号：F274;F7217  文献识别码：A  文章编号：

2096-3157（2020）08-0025-03

一、绪论

随着人们生活水平和健康意识的提高，新鲜牛奶的需求越来越多，对新鲜牛奶的品质要求也越来越高。“巴氏杀菌奶”具有“更新鲜”“更营养”的特点，受到了众多消费消费者的青睐[1]。近年来，由于“巴氏杀菌奶”的生产商越来越多，各种品牌的新鲜牛奶在口味上有一定的差距，消费者对不同口味的新鲜牛奶钟爱程度有差异，使得超市在进行新鲜牛奶的库存决策时变得更加的复杂。超市在进行新鲜牛奶的库存决策过程中受到多方面因素的影响，包括：资金、存储空间、品种数量、利润、保质期等[2]。超市需要科学制定库存决策，才能取得最大利润，提高顾客忠诚度。本文在研究影响新鲜牛奶的库存决策诸多因素的基础上，构建新鲜牛奶库存决策的多目标规划模型，希望提升超市在进行新鲜牛奶的库存决策的效果和决策层次，以实现超市库存控制的高效益。

二、多目標规划数学模型的构建

假定超市库存决策需要考虑f1（X），f2（X），……fn（X）等n个目标，X=（x1，x2，...xn）T是决策向量，x0。库存系统受到诸多因素的约束，包括：资金、储存空间等系统约束，以及品种数量、利润、平均保质期等目标约束。多目标规划的数学模型可以描述为：V-min（f1（X），f2（X），……fn（X））gi（X）o，i=1，2，……mhj（X）=o，j=1，2，……l

其中：gi（X）是目标约束，hj（X）是系统约束。

比较常用的用于求解多目标规划方法主要有约束法、功效系数法、评价函数法、目标规划法等[3]。本文应用winQSB软件下的目标函数法求解多目标规划问题。

目标规划是通过设定的问题的目标为基础，对目标顺序进行一一检查，尽可能使求解的结果达到设定的目标。目标之间存在相互对立是多目标规划经常遇到的问题。目标规划求解使得最优解即使不能实现全部目标，也使得的结果与目标的差距最小化，因此，目标规划的最优解也称为满意解。目标规划有两类偏差变量：未达到目标值的值称为负偏差变量，用d-表示;超过目标值的差值称为正偏差变量，用d+表示;d-0，d+0。目标规划的目标函数就是求得所有偏差变量的和最小值，即最接近目标。

目标规划的数学模型可以描述为：

minZ=∑Kk=1Pk（∑Ll=1ω-kld-l+∑Ll=1ω+kld+l）

∑nj=1aij·xjSymbolcB@

bi        （i=1，2，…m）∑nj=1clj·xj+d-l-d+l=gl  （l=1，2，…L）xj0           （j=1，2，…n）d-l，d+l0         （l=1，2，…L）

式中：Pk为第k级的优先因子，k=1，2，3，……K;ω-kl，ω+kl分别为赋予第l个目标约束的正负偏差变量的权系数;gl为目标的预期值，l=1，2，3，……L。

优先因子Pk可以利用两两比较法进行确定。首先将每个目标与其他目标进行对比，若Pv>Pu（1

K），表示Pv比Pu重要。然后计算位置处于左边的Pk的总数。最后，从大到小排列，最大的优先级最高，依次类推[4]。

三、模型应用

以某大型连锁超市在广州市的一个分店为例，实地收集相关数据，应用上述模型进行库存决策，以提高决策的有效性。新鲜牛奶的具体数据如表所示：

第一，超市的系统约束条件包括：存储空间和可用资金。存储空间主要是指具有保温能力的货架，以Y品种新鲜牛奶单位产品的占用空间为单位，共有180单位。可用资金是超市每天用于新鲜牛奶进货的流动资金，由于超市货品种类繁多，因此，用于每一种产品的进货资金每天金额都有严格控制，超市用于新鲜牛奶进货的资金额为2600元。根据超市每天的销售数据，新鲜牛奶的货架每天都能清空。超市希望得到最多的利润，利用线性规划可以求解出各种新鲜牛奶的最优库存量。但是由于顾客的需求受到多种因素的影响，所以不能单纯地追求利润最大化。因此，超市利用线性规划求解出最大利润后，取最大利润的80%作为目标利润。下面根据表中的数据，利用线性规划求解超市在追求利润最大化的目标下，各品种新鲜牛奶的库存决策。

由上述信息构建超市在追求利润最大化为目标下的线性规划模型，具体如下：

设xi为各品种新鲜牛奶的库存决策量，xi0，i=1，2，3，4，5。品种M的库存决策量为x1，X的库存决策量为x2，G的库存决策量为x3，Y的库存决策量为x4，W的库存决策量为x5。

目标函数：  MAZX=66x1+62x2+65x3+61x4+63x5

存储空间约束函数为：1.2x1+x2+x3+x4+x5

1.2x1+x2+x3+x4+x5+≤180

23.3x1+12.6x2+15.3x3+10.7x4+14.5x5≤2600

xi≥0，i=1，2，3，4，5

把上述线性规划数学模型代入winQSB软件求解，得到结果如图1所示：

由图1可知，在以追求利润最大化为唯一目标时，超市的库存策略是G品种新鲜牛奶146单位;Y品种新鲜牛奶34单位。其他品种均没有库存，超市可以获得约1163.2元的最大利润。超市需要考虑影响顾客需求的其他因素，设定最大利润的80%作为目标利润下限，因此，超市的利润目标约束为：

66x1+62x2+65x3+61x4+63x5≤930

改为目标规划的标准形式：

66x1+52x2+66x3+41x4+45x5+d-1=930

，即超市要尽量达到930元的目标利润。如果不能达到，那么负偏差变量d-1尽可能接近0。

第二，超市在财务方面的目标，除了利润以外，还有销售额的要求。超市希望获得最大的销售额，但是销售额最大化与利润最大化存在一定的矛盾，所以超市把最大销售额的85%作为目标。下面利用线性规划求解超市的最大销售额，数学模型如下：

MAZX=299x1+188x2+218x3+168x4+208x5

1.2x1+x2+x3+x4+x5≤180

23.3x1+12.6x2+15.3x3+10.7x4+14.5x5≤2600

xi≥0，i=1，2，3，4，5

把线性规划数学模型代入winQSB软件求解，得到结果图2所示：

由图2可知，在以销售额最大化为唯一目标时，超市的库存策略是：X品种新鲜牛奶6单位;G品种新鲜牛奶144单位;Y品种新鲜牛奶30单位，其它品种均没有库存，超市可以获得约3756元的最大销售额。超市设定最大销售额的85%作为目标下限，因此，超市的销售额目标约束为：

299x1+188x2+218x3+168x4+208x5≥3192

改为目标规划的标准形式：  299x1+188x2+218x3+168x4+208x5+d-2=3192

，  即超市要尽量达到3192元的目标利润。如果不能达到，那么负偏差变量d-2尽可能接近0。

第三，对于超市来说，商品品种越多，对顾客的吸引力越大。为了吸引更多的顾客，超市要求每一品种的新鲜牛奶库存量尽量达到10个单位以上，以满足不同顾客的需求。因此，超市在品种方面的目标约束为：

x1+d-3=10x2+d-4=10x3+d-5=10x4+d-6=10x5+d-7=10

另外，超市与品种G和品种Y的供应商签定战略合作伙伴关系，要求品种G和品种Y的库存量尽可能比其他品种多，并且品种的生产商位于广州市，要求品种Y的库存量是品种G的1.5倍。因此，目标约束为：

x3-x1+d-8=0x3-x2+d-9=0x3-x5+d-10=0x4-x1+d-11=0x4-x2+d-12=0x4-x5+d-13=01.5x3-x4+d-14-d+14=0

第四，整理上述目标约束，并对目标的优先级进行确定，共确定了四个层级的目标优先级。认为吸引更多的顾客最重要，战略合作伙伴关系第二重要，利润目标和销售额目标第三重要，品种G与品种Y数量比例第四重要。因此得到目标规划的数学模型：

MINZ*=P1（d-3+d-4+d-5+d-6+d-7）+P2（d-8+d-9+d-10+d-11+d-12+d-13）+P3（d-1+d-2）+P4（d-14+d+14）

6.6x1+6.2x2+6.5x3+6.1x4+6.3x5+d-1=93029.9x1+18.8x2+21.8x3+16.8x4+20.8x5+d-2=3192x1+d-3=10x2+d-4=10x3+d-5=10x4+d-6=10x5+d-7=10x3-x1+d-8=0x3-x2+d-9=0x3-x5+d-10=0x4-x1+d-11=0x4-x2+d-12=0x4-x5+d-13=01.5x3-x4+d-14-d+14=0xi10，i=1，2，3，3，4，5

把上述數学模型在winQSB软件上建模[5]，得到结果如图3所示：

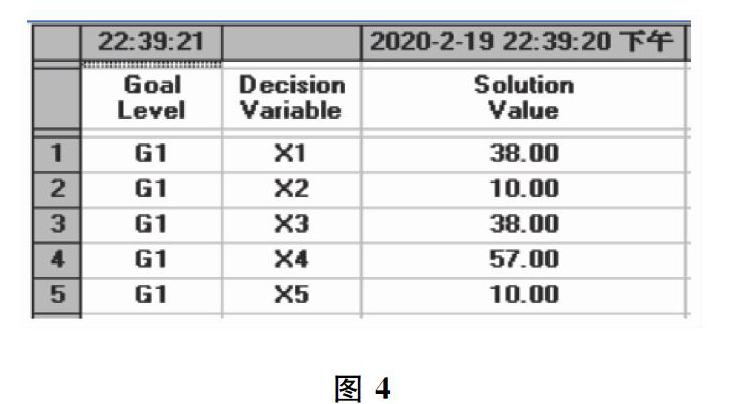
对图3进行求解，得到结果如图4所示：

由图4可知，超市的库存决策是：品种M的库存量38单位，品种X的库存量为10单位，品种的库存量为38单位，品种Y的库存量为57单位，品种W的库存量为10单位。

四、总结

新鲜牛奶由于其特殊的保管环境，超市库存决策的难点。本文分析了影响超市新鲜牛奶库存决策的影响因素的基础上，建立了多目标规划的一般模型。以广州市某超市的真实数据为例进行实例研究。首先利用线性规划法，确定了超市的利润目标和销售额目标。然后利用多目标规划理论，构建新鲜牛奶库存决策的多目标规划模型。最后应用winQSB20进行建模并求解，求解结果可以有效的解决超市对新鲜牛奶决策的多目标问题。

参考文献：

[1]王洁，杨江澜，刘款，高常凯河北省巴氏奶消费市场调研分析[J]黑龙江畜牧兽医，2018，（06）：14～18

[2]侯国栋，孙晓，王淑云，姜樱梅基于生鲜品库存模型的供应链协调机制研究[J]商业经济研究，2017，（15）：29～31

[3]李静，解强基于多目标规划的商业银行资产负债管理[J]统计与决策，2011，（14）：149～151

[4]宋雪莲基于多目标规划的联合库存管理研究[J]机械管理开发，2013，（02）：185～187

[5]刘孟晖基于非线性多目标规划的最优寿险投资组合模型[J]统计与决策，2011，（19）：52～54

[注]基金项目：广州工商学院2019年校级项目“基于系统动力学的两阶段价格生鲜品库存策略”（编号：KA201911）;2019年中国物流学会、中国物流与采购联合会研究课题“两阶段价格报童问题研究”（项目编号：2019CSLKT3-170）

作者简介：

陈见标，广州工商学院讲师;研究方向：冷链物流，供应链管理。