以问题思维为导向的小学数学教学

刘太祥

【摘  要】  以问题思维为导向的小学数学教学是尊重学生主体作用的表现，是提高其学习能力和综合素质发展的重要手段。在小学数学教学中，以问题思维为导向可培养学生逻辑思维能力，提升其数学学习能力。本文以“三角形的三边关系”知识为例，探讨了基于问题思维为导向的知识呈示、实践演示、互动交流和自主探究，改善思考模式，提升数学思维，提高数学核心素养。

【关键词】  思维导向;小学生数学;思考模式

以问题思维为导向的小学数学教学是尊重学生主体作用的表现，是提高其学习能力和综合素质发展的重要手段。教师首先需要对课程进行教学目标、教学重难点、教学过程的拟定，在教学过程中有条理地推进课程，培养学生自主提出问题和探究问题的能力。

一、教学目标：以问题思维为导向的小学数学教学的预设

教学目标的合理制定是提高学生课上学习效率的重要前提。教师在小学数学教学前，需根据课程标准提出具体问题，列出教学目标，并以其为标准，进行问题的设定以及教学深度的选择。

例如，以“三角形的三边关系”课程知识为例，教师在教学前需列好以下教学目标：

1.利用问题思维为导向的教学，提高学生观察、研究三角形三边关系的能力，使其理解三角形两边之和大于第三边知识内容。同时，充分利用课程内容，使学生思考生活中的相关案例。

2.通过该课程知识的学习，提高学生数学逻辑思维能力。

3.在研究三角形的三边关系的过程中，教师要调动学生学习积极性，使学生积极参与到数学学习中，并以小组形式进行学习，提高学生间的交流与合作，使学生在小组中取长补短，提高数学学习能力。

二、教学过程：以问题思维为导向的小学数学教学的实施

以问题思维为导向的小学数学教学需要结合课程内容，设计高价值的问题。设问式教学是利用小学生好奇的心理特性，集中学习注意力，使学生积极观察、思考问题，并找到解决问题的方法。该教学方法不但能够培养学生逻辑思维能力，还能够促进学生数学能力的提升。教师在应用问题教学时，可应用多媒体等设备进行教学，提高学生的数学学习能力。以下以四年级下册“三角形的三边关系”的教学为例。

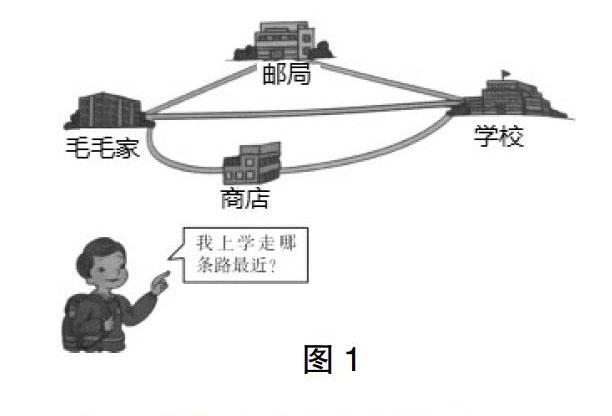
1.基于问题思维的知识呈示。教师在授课时，可先借助多媒体教学，向学生展示图1，并询问学生：“同学们，毛毛上学时，有几条路可以选择呢？”有学生回答：“毛毛直着走，就可以直接到达学校。”也有的学生回答：“毛毛可以先经过邮局，之后再到达学校。”还有的学生回答：“毛毛可以先经过商店，再到达学校。”教师可继续追问：“那图1中毛毛提出的问题，你们可以解答吗？”每位学生都争着发表自己的观点，教师可表扬学生积极回答问题，并进行引导：“在解决一个问题时，不单需要动脑，还需要学会动手，大家可在练习本上画一个简易图，并利用手中的尺子，进行测量，看看毛毛走哪一条路比较合适。”学生通过动手测量得出结果：直接走到学校距离最短。以问题思维为导向的小学数学教学方式可拓展学生学习思维，这种教学方式往往需要学生动手或者动脑来满足求知欲，这也无形之中培养了学生的主动学习能力。

2.基于问题思维的实践演示。教学过程中，以问题思维为导向，帮助学生在问题探索中积累经验，从而促进学生学习方法和学习能力的提升。

教学前，教师让每个学生准备三根小木棒，木棒的长度不能比10 cm长，不能比1 cm短。在教学时，教师可以让学生拿出学习工具，然后问学生：“同学们，三角形是由三条边首尾相连组成的封闭图形，那你们手中的三根小棒，可以组成一个三角形吗？”有的学生说可以，有的学生说不可以。对此，教师可让学生做个小实验，引导其自行观察，如图2。

教师提问：“为什么三根小棒有的可以组成三角形，而有的不能呢？”让学生自己动手实践，观察三角形三边关系。实践探索知识可开阔学生大脑思维，学生在进行试验的过程中不但获得了知识，也对知识获得的方法有了更加深刻的认知。在给予学生一定的实践和思考时间后，教师可以问学生：“四组当中，哪一组可以组成三角形呢？”得出答案是第一组和第四组。

教师顺理成章地引领学生探究三角形三条边之间的规律。这种教学方式的应用可极大提高了学生实践思考能力，促進其良好学习方法的养成和学习能力的提高。

3.基于问题思维的互动交流。教师要充分利用学生间互动生成的课程资源。例如教师可先在黑板上画出两个大圈，一个圈中写上“能组成”，另一个圈中写上“不能组成”。然后让学生自己动手拼三角形，并记录三角形的三边数据，随后教师挑选学生将得出的数据写在对应的圆圈中。最后，全班同学一起探讨，圆圈中的数据是否正确，这可以营造良好的学习氛围，增强其探究问题的能力。

教师追问：“根据圆圈中不能组成三角形的数据可知道三角形两边之和相等或小于第三边，是不能组成三角形的，那三角形的三边处于什么条件下，才能拼组成三角形呢？”随后教师带领全班同学共同探究圆圈中可组成三角形的数据。最后得出答案，在三角形两边之和大于第三边的时候可组成三角形。

在此基础上，教师继续让学生探究三边之间的关系，以6、7、8数据为例，让学生自行得出：6+7>8，6+8>7，7+8>6，由此引导其找到三角形三边关系的条件——“任意”。最后得出结论：“三角形任意两边之和大于第三边”。全班同学一起探究问题的方法可营造良好学习氛围，可加强学生对该课程知识的理解，这种思维共振的形式能够让学生更好地认识三角形的诸多性质。

4.基于问题思维的自主探究。教是为了达到不需要教，教学中必须着力培养学生的自主学习、自主探究的能力。三角形两边之和小于第三边时不能组成三角形的结论得出后，教师还需继续引导：“同学们可以从数学符号着手继续研究问题。”有的学生会思考：“那三角形两边之和等于第三边时，可不可以组成三角形呢？”“三角形两边之和大于第三边时，能不能组成三角形呢？”自问自究中，深入探究，得出结论。这样的探究，可以帮助学生养成良好的学习习惯，促进自学能力的提高。

最后，根据本课得出的结论，教师可将学生思路领回到课始，应用三角形的三边关系，学生可以发现：“毛毛走中间的路段距离最近。”这样不仅可巩固其学到的理论知识，还可促进与实践生活的联系，学以致用，提高对数学知识的体认。以问题思维为导向的数学教学有助于学生将理论与实际相联系，改善思考模式，提升数学思维，提高数学核心素养。

【参考文献】

[1]谈静.问题引领，激活数学课堂[J].名师在线，2020（1）.

[2]管小冬.注重经历过程，发展问题意识[J].小学数学教育，2018（12）.