运用几何画板动态展示数学中的抽象定义

何洪英

摘要：将信息技术与数学课程深度融合是高中数学新课标提出的理念。为了进一步推动该理念的实现，文章主要介绍了利用几何画板软件，对平面解析几何中的抽象定义进行情境创设，从而让数学课堂更生动、形象、直观，有效提高学生的核心素养。

关键词：新课标;数学;几何画板;深度融合

中图分类号：G642 文献标识码：A

文章编号：1009-3044（2020）14-0226-02

中华人民共和国教育部制定的2017版《普通高中数学课程标准》的基本理念中提出：“提倡独立思考、自主学习、合作交流等多种学习方式，激发学习数学的兴趣，养成良好的学习习惯，促进学生实践能力和创新意识的发展。注重信息技术与数学课程的深度融合，提高教学的实效性。”要将信息技术与数学课程深度融合，就必须使用强大的计算机软件辅助数学教学，虽然现在大家都提倡让计算机走进教室，但很多中学老师对计算机软件的认识和运用水平都跟不上，所以导致在中学数学教学中，计算机软件辅助教学并没有得到广泛运用。

为此，本文主要介绍一款优秀的数学软件——《几何画板》，在平面解析几何教学中对抽象定义的动态演示，抛砖引玉，以实际案例使更多一线教师认识并学习相应的软件，以更好实现信息技术与数学课程的深度融合。

1软件介绍

《几何画板5.0》是最优秀的数学、物理教学软件之一。几何画板操作简单，具有强大的图形和图像功能，能构造出各种几何图形及解析几何中的所有曲线，也能构造出任意函数的图像，同时，它具有方便的动画功能，能够制作出平移、旋转、缩放、反射等各种动画，还能对动态的对象进行追踪，并显示追踪的轨迹。

2在平面解析几何中的具体应用

《普通高中数学课程标准》的课程内容指出“平面解析几何的教学中，应引导学生经历以下过程：首先，通过实例了解几何图形的背景，例如通过行星运行轨道、抛物运动轨迹等，使学生了解圆锥曲线的背景与应用;进而，结合情境清晰地描述图形的几何特征与问题，例如椭圆是到两个定点的距离之和为定长的动点的轨迹等。“

在这里，椭圆的定义用文字描述非常的抽象，用传统教学手段也不好演示椭圆的形成，为了更好地掌握椭圆的定义，可以利用几何画板创设情境、动态演示椭圆的形成过程，让学生通过自主探究自己推出结论并深刻理解定义。

2.1椭圆的定义

椭圆定义：平面上到两个定点的距离之和为定长（该定长大于两点间的距离）的动点的轨迹。这两个定点也称为椭圆的焦点，焦点之间的距离叫作焦距。

要动态性展示动点的轨迹形成过程，可以使用《几何画板》的“追踪”功能，具体实现方法如下。

（1）单击[线段工具]，在画板适当位置绘制出一条线段AB。单击[点工具]，在线段AB上取一点c。如此点c即是线段AB上的点并只能在AB上运动，而不管如何运动，点C到两个定点A、B的距离之和始终为定长（线段AB的长）。

（2）选中点A、点c，执行[构造]I[线段]，选中点c、点B，执行[构造]I[线段]，分别构造出线段Ac和线段CB。

（3）单击[点工具]，在画板适当位置任取一点D，选中点D和线段Ac，执行[构造]I[以圆心和半径绘圆]命令，绘制一个圆D。

（4）单击[点工具]，在画板适当位置任取一点E，使DE的距离小于线段AB的长，选中点E和线段cB，执行[构造]l[以圆心和半径绘圆]命令，绘制一个圆E。

说明：点D和点E即是两个定点，使DE的距离小于线段AB的长，是为了满足定义中的条件“定长大于两点间的距离”。绘出的效果如图1所示。

（5）选中两个圆，执行[构造]I[交点]命令，构造出两个圆的交点F和G，这样两个交点到定点D和E的距离之和等于线段AB的长。拖动点C在线段AB上运动，可以发现两个圆的半径随之改变，但不论如何改变，两个圆的交点F和G到定点D和E的距离之和始终等于定长（线段AB的长）。

至此就构造出了定义的前提条件：到两个定点的距离之和等于定长的动点。后面只需再追踪动点F和G，就可以看到满足条件的动点的轨迹。

（6）选中点c，执行[编辑]I[操作类按钮]I[动画]命令，生成点C的动画按钮。

（7）选中点F和G，执行[显示]I[追踪交点]命令。

单击“点c的动画”按钮，就可以展示出点c的运动，导致交点的运动，追踪交点进而形成椭圆轨迹的动态过程，学生可以自主探索，如改变线段AB的长度，改变点D和E的位置，拖动改变点C的位置，在这个过程中学生自己就能得出结论并深刻理解椭圆的定义。

最终效果如图2所示。

2.2抛物线的定义

抛物线定义：平面内到一个定点和一条定直线的距离相等的点的轨迹。

根据定义，首先应该在画板上构造出一条定直线和一个定点。具体实现过程如下：

（1）构造定直线1。单击[直线工具]，绘制一条竖直直线AB，选中点A和B，执行[显示]I[隐藏点]命令隐藏点A和B。

（2）构造定点。单击[点工具]，在适当位置绘制绘制点c。如图3所示。

（3）到一个定点和一条定直线的距离相等的点肯定在定直线的任意垂线上，因此第三步构造定直线的任意垂线。单击[点工具]在定直线上取一点D，选中点D和定直线，执行[构造]I[垂线]命令，构造出过点D的定直线的垂线k。因为点D是定直线上的点，可以在直线上任意运动，因此当点D在定直线上运动时，过点D的定直线的垂线即是定直线的任意垂线。

此时只需找出垂线上的一点到点D和到点C的距离相等，显然这个点只可能在线段cD的垂直平分线上。

（4）选中点c和D，执行[构造]I[线段]命令，构造出线段cD。选中线段cD，执行[构造]I[中点]命令，构造出线段cD的中点E。

（5）选中线段cD和中点E，执行[构造]I[垂线]命令，构造出线段CD的垂直平分线i。

（6）单击垂线k和垂直平分线j的交点位置做出两条直线的交点F。显然点F到定直线l和到定点c的距离相等（都等于线段CD的长）。而当点D在直线上运动时，点F的位置随之改变，但始终保持到一个定点和一条定直线的距离相等，因此只需制作点D的动画，追踪点F的变化轨迹就完成了定义的情境设定。

（7）选中点D，执行[编辑]I[操作类按钮]I[动画]命令，生成点D的动画按钮。

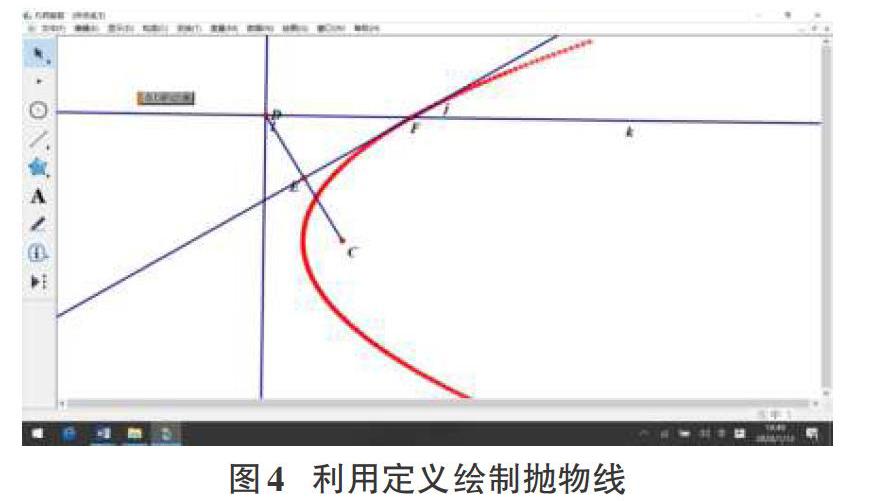
（8）选中点F，执行[显示]I[追踪交点]命令。最终效果如图4所示。

单击“点D的动画”按钮，就可以展示出随着点D运动，导致交点F运动而形成抛物线軌迹的动态过程。

通过上面两个简单实例，可以发现传统手段不好解释的一些数学定义，用《几何画板》软件却能轻松地模拟出具体情境，形象直观，让学生从对具体情境的探究中自己就能推出定义，自然就达到了深刻理解掌握定义的目的。

3结束语

在数学概念与理论的教学中，几何画板既能创设隋境又能让学生主动参与，引导学生亲历知识的发生、发展过程，即数学模式的建构过程，使抽象、枯燥的数学概念变得直观、形象，所以能有效地激发学生的学习兴趣;同时在学习过程中，养成独立思考、积极探索的习惯，让学生通过探索、反思、修改、完善，体验数学发现和创造的历程，培养他们的创新意识，并品尝成功的快乐。

几何画板与课程整合应用于创设情境、自主探究、动态演示、概念教学、辅助解题和参数讨论等方面。本文例谈只是应用的某些方面，希望以此能让更多老师了解和认识该软件，以促进信息技术与数学课程的深度融合。