利用数形结合提高学生解决实际问题的能力

季艳秋

【摘要】小学生的思维是以形象思维为主的。在学生学习解决实际问题的过程中，教师需要采用数形结合的方式，运用线段图、示意图、对应图、解析图式等方法，将抽象的知识具象化，使学生形象地理解题意，获得对事物的整体认识。同时，教师应直接揭示实际问题中的数量关系，引导学生积极思考，从而使其迅速地找到解决问题的方法，进而提高学生解决問题的能力。数形结合思想是根据数与形之间的对应关系，通过数与形的相互转化，将抽象的数学问题与直观的图形结合起来解决问题的思想方法。数形结合思想有利于学生分析题中数量之间的关系，能拓宽学生的思路，使学生迅速找到解决问题的方法，从而提升学生分析问题和解决问题的能力。因此，在实际教学中，教师应充分利用数形结合的思想，不断提升学生的学习能力。

【关键词】数形结合;直观;解决实际问题

解决问题教学一直以来都是小学数学教学的重点与难点。《义务教育数学课程标准（2011年版）》中指出：“应使学生经历从实际问题中抽象出数量关系，并运用所学知识解决问题的过程，学会分析问题和解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识。”小学生的思维是以具体的形象思维为主的，在学习解决实际问题的过程中，很难把握数学问题的本质，对问题的条件和结论之间的内在联系常常是一知半解，解决问题时也常常不知所措。

华罗庚先生曾指出：“数缺形时少直觉，形少数时难入微;数形结合百般好，隔离分家万事休。”在应用数形结合思想方法解决实际问题时，学生能把“数”与“形”很好地结合起来，这样，一些看似复杂的实际问题就会迎刃而解。数形结合对教师来讲是一种教学方法、教学策略;对学生来讲则是一种形成良好的数学意识和思维的重要学习方法。数学教师系统地运用数形结合思想进行教学，在教学中注重发挥数形结合的作用是非常必要的。

一、数形结合方法的由来

早在数学被抽象、分离为一门学科之前，人们在生活中测量长度、计算物体面积和体积时，就已经把数和形结合起来了。在宋元时期，我国古代数学家已经系统地引进了几何问题代数化的方法，用代数式描述某些几何特征，把图形中的几何关系描述成代数关系。这些都说明了数形结合方法有着悠久的历史。在小学数学教学中，数形结合思想能提升学生分析问题和解决问题的能力。

二、数形结合教学策略

如何在数学教学中发挥数形结合的作用，提高学生解决问题的能力呢？笔者认为，数学教师可以从以下几方面做起。

1.画线段图，迅速发现数量关系

用线段图来帮助学生分析题意、明确数量关系，是行之有效的重要解题手段之一。运用线段图进行实际问题的教学，可以把题目中的已知信息和问题间的联系直观化，便于学生观察、分析数量关系，为其获得解题思路铺平道路。

例如，在三年级上册两步计算的实际问题的教学中，教师利用线段图来帮助学生理解题意，更容易突破教学难点。

例题：妈妈的年龄是小芳的4倍，妈妈的年龄比小芳大27岁，你知道妈妈和小芳的年龄各是多少岁吗？

在读题、理解题意的过程中，笔者发现大多数学生无法迅速找到已知信息与问题间的联系，解决问题有困难。此时，笔者引导学生根据题意画出线段图（见图1）。

借助线段图，学生一目了然看出妈妈的年龄比小芳多了4-1=3份，3份对应的岁数是27岁，由此可以计算出一份是多少岁，即小芳的年龄是27÷3=9（岁），妈妈的年龄是9×4=36（岁），或9+27=36（岁）。

2.画示意图，整体把握问题实质

“示意”是揭示事实情节含义的意思。在教学活动中，有些实际问题的数量关系比较复杂，事理难以把握，这就需要教师引导学生画示意图来理解、分析题意。示意图不要求像线段图那样准确地反映题目的已知信息和问题及相互关系，它仅仅要求通过示意，进行直接的本质理解和综合的整体判断，给学生提供寻找解决问题途径的方向。

例如，解决与面积有关的实际问题：一个长方形菜园，长25米，宽10米，在菜园的四周建一条宽2米的道路，求道路的面积是多少。

对于学生来讲，如果仅仅依靠文字叙述来弄清求的是哪一部分的面积，是比较困难的，也无法用画线段图的方法解决问题。此时，教师只要指导学生动手画出菜园道路修建情况的示意图（见图2），并将相关的已知信息进行标注，问题就迎刃而解了。

学生能以自己所画的菜园道路修建情况示意图为切入点，整理解决问题的思路和步骤，研究出不同的计算菜园一周道路的面积的方法。如：（25+4）×（10+4）-25×10=156（平方米）;（25+2）×2×2+（10+2）×2×2=156（平方米）;25×2×2+10×2×2+2×2×4=156（平方米）……

3.画对应图，具体认识内在规律

在解决一些按规律变化的实际问题的过程中，教师以对应图的形式反映事物及其变化过程，能让学生迅速地从众多的信息中发现事物的变化规律。在教学中，教师应善于指导学生收集整理信息，借助直观的图形把题目中的已知条件和变化过程用对应图的方式呈现出来，帮助学生具体地认识事物及其变化规律，从而使学生顺利地找出解题思路及解决问题的方法。

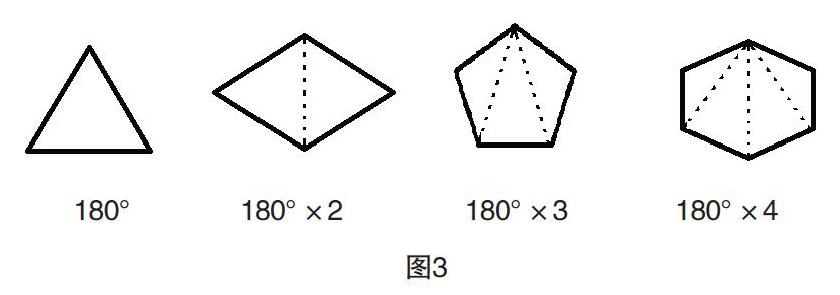
例如，我们已经学过三角形的内角和，要了解四边形、五边形、六边形……n边形的内角和，可以尝试把多边形分成若干个三角形，按序画出对应图。学生可以通过观察直观图（见图3），从了解图形边数的变化规律和内角和的变化规律入手，进而观察和发现多边形内角和与其边数之间的内在联系，找到其中蕴含的规律：n边形内角和=180°×（边数-2）。

4.列解析图式，回归起点另辟蹊径

解析图式是分析数量间的相互关系、寻找解题途径的一种图式。它一般适用于解决数量关系比较复杂、难度较大的实际问题。教师可以用解析图式来对学生进行直觉的启发，这样，即使是数量关系复杂而隐蔽的题目，学生的解题思路也会一目了然、不讲自明。

例题：面值分别为2元、5元的人民币共有8张，合计31元。那么2元和5元的人民币各有几张？

这道题只用一般的从条件和问题入手的策略，很多学生无法找到解题的突破口。如果学生结合假设的方法画解析图式，那么问题就不会显得复杂难懂了。

假设8张都是2元的人民币，应当是16元。画出分析图，如图4所示。

16元与31元相差15元，再把15元分别加在2元上，每个加3元，使之成为5元，如图5所示。

通过解析图式，学生可以知道面值为5元的人民币有5张，面值为2元的人民币有3张。学生学会了这种办法，再遇到同样的问题就不会束手无策了。

总之，在解决问题的教学中运用数形结合的思想，通过形象思维这个中间环节直接揭示题中的等量关系，是帮助学生理解某些抽象关系、促使学生积极思考以解决问题的行之有效的方法之一。只要教师注意选择恰当的教学方法，并通过一定形式的训练，培养学生思维的灵活性，使学生养成良好的学习习惯，那么学生解决问题的能力定会不断提高。

【参考文献】

胡颖.数形结合在小学第二学段教学中的运用研究[D].镇江：江苏大学，2019.

徐玲玲.善用数形结合，培养核心素养[J].小学教学参考，2018（11）：67-68.

刘玉桂.浅谈数形结合在小学数学教学中的应用[J].新课程学习（下），2015（08）：64.

王伟.浅谈数形结合在小学数学中的应用[J].中华少年，2016（05）：130.

毛建铭.重视数形结合  培养数学素养[J].名师在线，2018（01）：64-65.

施艳艳.浅谈数形结合在小学数学中的运用[J].中国校外教育，2014（16）：119.

李淑凤.数形结合在小学数学教学中的思想渗透分析[J].课程教育研究：新教师教学，2018（11）：47.

張艳红.数形结合思想在小学数学教学中的应用[D].济南：山东师范大学，2016.

连作鹏.小学数学教学中数形结合思想教学模式初探[J].中学课程辅导（教师教育），2016（06）：52.