基于数学史的数学文化内涵实证研究
2020-07-03余庆纯汪晓勤
余庆纯,汪晓勤
基于数学史的数学文化内涵实证研究
余庆纯1,汪晓勤2
(1.华东师范大学 数学科学学院,上海 200241;2.华东师范大学 教师教育学院,上海 200062)
采用德尔菲法、文本分析法开展质性研究,通过对“基于数学史的数学文化”内涵分析框架的论证与修正、2012—2018年间的20个高中HPM课例分析发现,基于数学史的数学文化内涵可分成知识源流、学科联系、社会角色、审美娱乐与多元文化5个维度,且在教学实践中5个维度运用不均衡.为了更好地揭示数学教学中数学文化的教育价值,教师需要注重历史学习,夯实理论基础,立足教育现实,加强实证研究.
德尔菲法;文本分析法;数学史;数学文化;HPM课例
1 问题提出
关于数学文化的内涵,很多学者都曾作过探讨.顾沛在谈及“数学文化”时,从两个方面进行阐述:“狭义的数学文化内涵是指数学思想、精神、方法、观点以及它们的形成和发展;广义上的数学文化除上述内涵外,还包含数学家、数学史、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系等.”[1]代钦基于一般文化的各种定义和数学学科以及数学与人类其他文化关系,进一步提出:数学文化是数学知识、思想方法及其在人类活动的应用以及与数学有关的民俗习惯和信仰的总和,并指出数学文化具有规范特征、审美特征、认知特征、历史特征、价值特征[2].对于数学文化的5个特征之间的联系,有待深入研究.后来,杨豫晖、宋乃庆等学者总结了国内已有的数学文化理论研究成果,分别从数学学科、文化、数学共同体、数学活动、系统等5个角度对数学文化的内涵进行述评,提炼出“数学文化”的概念界定,即指一群人(数学家),当他们从事数学活动时,遵循共同的数学规则,经过长期的、历史的沉淀,形成了许多关于数学知识、精神、思想方法、思维方式等的共同约定的总和,并指出数学文化具有思维训练、德育、美育等价值[3].可见,对于“数学文化”的内涵,没有公认的概念界定,不同研究者均有不同侧重,且对数学文化的价值探讨更是丰富多元.
《普通高中数学课程标准(2017年版)》(以下简称《标准》)提出:数学文化是指数学的思想、精神、语言、方法、观点以及它们的形成和发展,还包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动[4].可见,数学史是一个巨大的宝藏,其中蕴含了数学的思想、方法、精神及其发生和演进过程,揭示了数学家的文化活动以及数学在人类文明进步中的巨大作用,因而成了数学文化不可分割的重要组成部分.《标准》在“课程目标”中指出:“通过高中数学课程的学习,提高学习数学的兴趣,增强学好数学的自信心,养成良好的数学学习习惯;树立敢于质疑、善于思考、严谨求实的科学精神;认识数学的科学价值、应用价值、文化价值和审美价值.”[4]同时,在“教学建议”中要求:“在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中,引导学生了解数学的发展历程,认识数学在科学技术、社会发展中的作用,感悟数学的价值,提升学生的科学精神、应用意识和人文素养;将数学文化融入教学,有利于激发学生的数学学习兴趣,有利于学生进一步理解数学,有利于开拓学生视野、提升数学学科核心素养.”[4]因此,如何在数学课程实施与教学实践中体现数学文化的教育价值,是数学教育工作者和一线教师热切关注的重要课题之一.
HPM(数学史与数学教育之间的关系)视角下的数学教学受到越来越多一线教师的关注,相关的HPM课例也日益增多.实践证明:数学史融入数学教学,有助于建构知识之谐,彰显方法之美,营造探究之乐,实现能力之助,展示文化之魅,达成德育之效[5].然而,HPM教学实践中依旧存在“高评价、低运用”的困境.张奠宙先生曾指出:数学教学往往局限于一个概念、一个定理、一种思想的局部历史的介绍,缺乏宏观的历史进程的综合性描述.实际上用宏观的数学史进程可以更深刻地揭示数学的含义,加深对数学知识的文化理解[6].目前,人们对数学史的文化价值的理解还不够深刻和全面.
有鉴于此,基于《标准》中“数学文化”的概念,对“基于数学史的数学文化”内涵分析框架开展深入的论证与修正,并根据该框架对高中HPM课例进行分析,试图回答:高中HPM课例中体现了哪些数学文化内涵?数学文化在不同维度上的分布情况有何特点?是否检验了“基于数学史的数学文化”内涵分析框架的客观合理性?对今日教学实践与研究有何启示?
2 研究方法与设计
以质性研究为主,采用德尔菲法(Delphi method)、文本分析法(text analysis)开展研究.德尔菲法(Delphi method)最初是由奥拉夫·赫尔默(Olaf Helmer)和诺曼·达尔基(Norman Dalkey)在20世纪50年代提出,后来该方法广泛用于教育评价指标体系的构建、评价与预测等研究领域[7].德尔菲法是一种有效的科学研究方法,本质上采用背对背的通信方式来征询专家组成员的意见,经过反复征询、归纳、修正,最后使专家组成员的意见趋于一致[7].文本分析法(text analysis)起源于20世纪40年代,是指基于文本的内容进行阐述、分析、论证与评价等.库卡特(Kuckartz)曾把定性的文本分析分为3大类:构建式文本分析(type- building text analysis)、主题式定性文本分析(thematic qualitative text analysis)与评价式定性文本分析(evaluative qualitative text analysis)[8].为符合HPM课例的研究要求[9],采用评价式定性文本分析,研究设计如下.
(1)框架的论证与修正.基于《标准》所提出的数学4类价值以及西方学者总结的数学史教育价值提出了“基于数学史的数学文化”内涵分析框架[10].为检验分析框架的客观合理性,研究采用德尔菲法,以访谈、研讨等形式对该分析框架进行剖析与论证,旨在进一步修正该分析框架.
(2)课例分析.根据HPM课例的研究要求,对收集的2012—2018年的高中HPM课例进行筛选,选取出符合要求的20个高中HPM课例作为研究对象,分析课例中的基于数学史的数学文化内涵及其在不同维度上的分布特点.
3 框架论证与修正
3.1 框架介绍
基于《标准》所提出的数学4类价值以及西方学者总结的数学史教育价值,可以将课堂数学教学中的数学文化内涵分成知识源流、学科联系、社会角色、审美娱乐和多元文化5个维度[10].“知识源流”是指某个知识点的历史演进过程中所涉及的人物与事件、概念与术语、问题与求解、命题与证明等.“学科联系”是指数学与其它学科之间的关联.数学乃是人类的文化活动,这种活动与人类其它文化活动水乳交融、不可分割,数学史揭示了数学与其它学科之间的密切联系[11].“社会角色”是指数学在人类生活、科学技术、社会发展中的贡献和意义.数学史“有助于解释数学在社会中的作用”[12].“审美娱乐”是指数学美(包括对称美、奇异美、简洁美、统一美等)与趣味数学.《标准》在“美与数学”课程中指出:“学会审美不仅可以陶冶情操,而且能够改善思维品质.”[4]数学史展现出人类对于美的追求、对于趣味的倾向性伴随着数学的诞生而诞生,“促进数学发展的不仅是实用性因素,而且还有美学标准、智力好奇、趣味娱乐等因素”[11].“多元文化”是指不同文明、不同地域的数学家在同一数学课题上的贡献与意义,以及与数学相关的人文活动[10].数学从来不是某个人、某个文明、某个国家或地区的专利,不同文化都对数学发展产生过影响,数学在不同时空的历史演进也是数学学习的目标[13].
基于《标准》中数学价值的表述[4],尝试界定数学4类价值的内涵(如表1所示).

表1 数学4类价值的内涵与《课标》中的相应表述
“基于数学史的数学文化”内涵分析框架[10]给出了基于数学史的数学文化内涵与《标准》所提出的数学4类价值之间的关系(见图1).
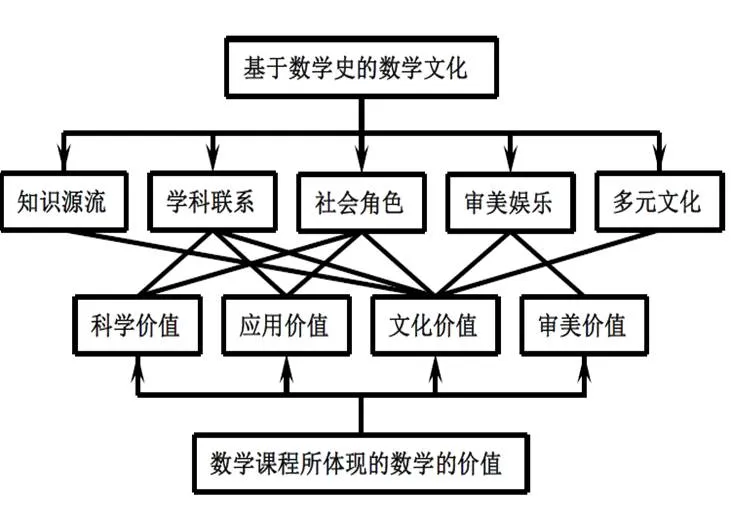
图1 “基于数学史的数学文化”内涵分析框架
3.2 框架论证与修正
为检验分析框架的客观合理性,采用德尔菲法.参与对象分别是两位高校研究者与6位一线专家型数学教师或教研员(基本信息如表2),均有研究数学史与数学文化的教研经历,具有一定的代表性.
该研究流程分为3个环节:开放式访谈、评价式研讨、复核式访谈.开放式访谈采用背对背的形式,了解各位老师对数学史与数学文化的研究情况;评价式研讨,主要由8位老师针对“基于数学史的数学文化”内涵分析框架进行线上多轮研讨、论证与反馈;复核式访谈是基于评价式研讨的内容,对各位老师进行针对性地回访与复核.

表2 访谈人员的基本信息
基于德尔菲法的咨询论证,得出如下结论.
(1)基于数学史的数学文化不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值[4],发展数学素养,承载着落实立德树人的根本任务.
(2)“基于数学史的数学文化”内涵分析框架关注“知识源流”与“多元文化”的互融互通.前者是时间纵轴,属于数学文化研究,需求深,帮助从数学内部的视角来了解数学中的文化.后者是空间横轴,属于数学文化比较,需求广,帮助从数学外部的视角来认识文化中的数学.
(3)“学科联系”从历史视角连结数学与其它学科(如哲学、文学、天文学等)的知识脉络,“社会角色”通过数学史揭示数学的社会价值与意义,二者居于社会发展的演进,凸显跨学科的文化交融.
(4)“审美娱乐”包含数学美与趣味数学.数学美横跨“文化中的数学”与“数学中的文化”,对称美、奇异美、简洁美、统一美是数学审美的内隐模式,而借助数学表现出审美的外显模式.趣味数学不仅展现数学知识的妙趣横生,激发数学学习兴趣,助力智力培育,而且趣味数学中历史与文化相映成趣,令人回味无穷.两者均是数学文化相当重要的组成部分.
(5)“基于数学史的数学文化”内涵分析框架既扎根于数学史的教育价值与高中新课程标准的新要求,又为数学文化融入课程、落实到教学提供指导,具有“上通理论、下达实践”的特点,具有一定的客观合理性.
基于如上结论,对“基于数学史的数学文化”内涵分析框架做进一步修正(如图2).
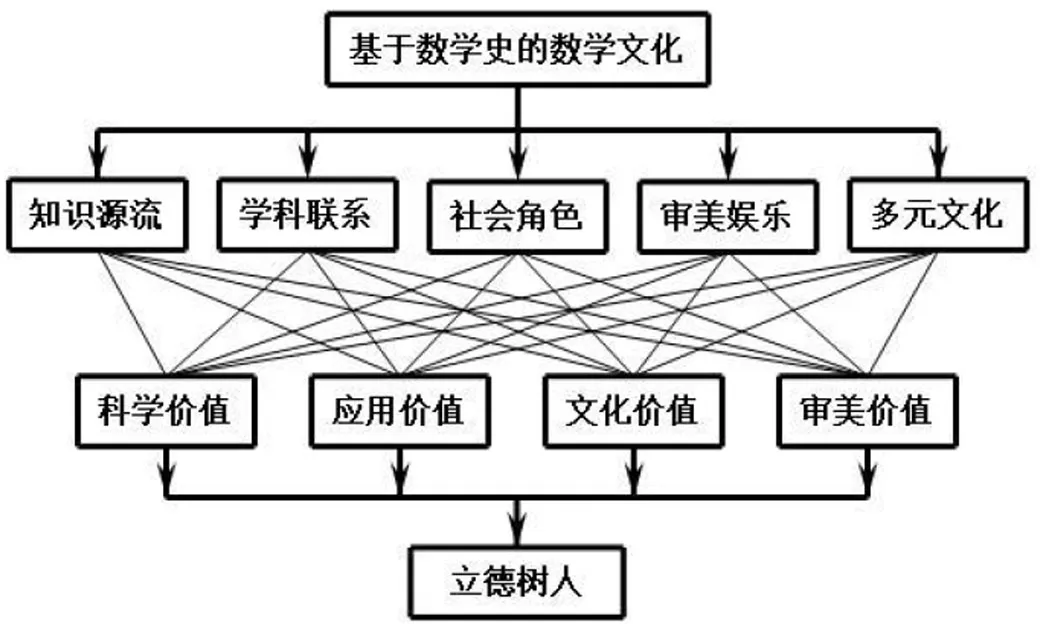
图2 修正的“基于数学史的数学文化”内涵分析框架
4 课例分析
4.1 课例选取
HPM视角下的数学教学,是指借鉴数学知识的发生发展、再现历史上的数学思想方法、采用适当的方式运用数学史料以提升教学质量、丰富教育价值的一种教学方式.其所形成的教学课例简称为HPM课例.
依据HPM课例研究中史料的适切性、应用方式的多元性等要求,以数学史融入数学教学的4种运用方式与5项融入原则作为高中HPM课例的筛选条件[9],附加式、复制式、顺应式和重构式等4种方式分别以1、2、3和4来编码,科学性、可学性、有效性、趣味性和人文性等5项原则分别以a、b、c、d和e来编码.经过双人编码、研讨与校对,筛选出2012—2018年间发表的具有代表性的20个高中HPM课例[14-33]作为研究对象(详见表3).

表3 20个高中HPM课例的基本信息

续表3 20个高中HPM课例的基本信息
按照《标准》分类,20个课例的课题分属函数、几何与代数、概率与统计、微积分等4个领域.其中,19个课例属于新授课,1个课例是复习课.绝大多数课例是由HPM学习共同体(由高校HPM研究者和中学一线数学教师组成)依照“选题与准备”“研讨与设计”“实施与反馈”“整理与写作”4个环节合作开发.
4.2 课例中的数学文化内涵
4.2.1 知识源流
20个HPM课例所涉及的“知识源流”维度大致可分成人物与事件、概念与术语、命题与证明、问题与求解等4个子维度.图3给出了“知识源流”各子维度的频数分布.
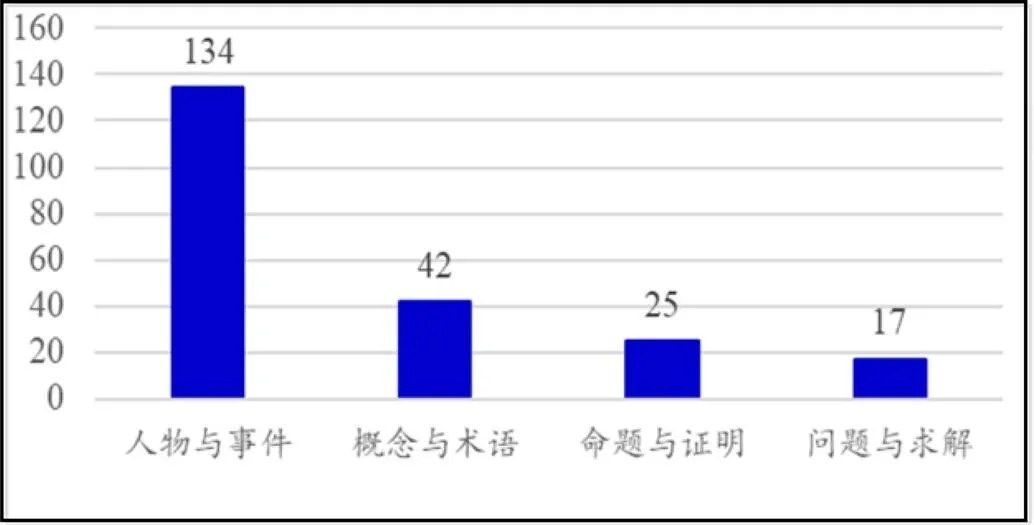
图3 “知识源流”各子维度的频数分布
课例“函数的概念”[14]参照历史,再现了函数概念从“解析式”定义—“变量依赖关系”定义—“变量对应关系”定义—“集合对应关系”定义的演进过程.课例“对数的概念”[15]涉及苏格兰数学家纳皮尔(J. Napier,1550—1617)发明对数的事件,还运用了古巴比伦泥版上的利息问题作为应用题.课例“点到直线的距离”[27]引入20世纪中叶西方教科书中的最值法和三角形面积法.在课例“椭圆的定义”[28]中,学生通过探究,经历了从椭圆截面定义到课本上的动点轨迹定义(第一定义)的过程.课例“数系的扩充与复数的引入”[30]向学生呈现了16世纪意大利数学家邦贝利(R. Bombelli,1526—1572)在求解三次方程时所遇到的“矛盾”.
4.2.2 学科联系
课例中,数学与文学、物理学、建筑学、天文学等学科具有“学科联系”.
课例“数列的概念”[17]以苏轼《水调歌头•明月几时有》中的经典名句“人有悲欢离合,月有阴晴圆缺”,指出“月相变化”中蕴含的数列规律.在课例“任意角”[19]中,教师引入白居易“离离原上草,一岁一枯荣,野火烧不尽,春风吹又生”的诗句来激发学生思考生活中常见的周期现象.可见,数学与文学相互渗透,这些古诗词的意境蕴含着数学抽象思维与文学形象思维之间的奇妙联系,彰显了数学的文化之魅.
课例“导数几何意义”[32]借鉴17世纪促使数学家研究切线的3类问题,设计“光在曲面上的反射”“曲线运动的速度方向”“拱桥的坡度”等问题情境,展现了数学与物理学、建筑学等学科息息相关.课例“导数的应用”[33]中,教师引入“费马原理(最小光程原理)”,通过导数推导出“折射定律”,揭示了数学与物理学的密切关系.
课例“数列概念”[17]通过意大利天文学家皮亚齐(G. Piazzi,1746—1826)发现谷神星的故事,体会数列推动天文学的发展.课例“正弦定理”[22]以在新知引入环节介绍10世纪阿拉伯天文学家阿尔•库希(Al-Kuhi,约940—1000)的流星测量方案,激发学生探究流星高度的学习动机,引入正弦定理;在知识应用环节,回顾、解决流星测量问题,展现数学与天文学之间的紧密联系.
4.2.3 社会角色
课例“数列概念”[17]通过两河流域泥版上的月相表,说明数学在古人的生产、生活中的巨大作用:抬头望月,日期可计,春耕秋收,井然有序.在课例“任意角”[19]的新知探究部分,教师引入古代计时仪器日晷与《周髀算经》中测量四季的方法,引导学生感受静态角与动态角在确定时间上的不同作用.
课例“抛物线的概念”[29]以古希腊人利用凹面镜原理采集火种的故事,说明抛物线的社会角色.在课例“导数的应用”[33]中,教师借鉴历史编制导数在生产设计、交通运输、通讯网络等领域的应用问题,体会微积分在现实生活中的重要应用.
4.2.4 审美娱乐
基于趣味数学方面,课例“数列概念”[17]将历史上著名的“约瑟夫问题”改编成“找位置”趣味游戏,让学生在游戏中体会数列的“序”的本质特征;课例“递推数列”[18]则利用“汉诺塔游戏”来引出递推数列概念,寓理于“做”.可见,历史上的趣味数学问题可以在高中数学课堂上大放光彩.
4.2.5 多元文化
课例“函数的概念”[14]展示了西方数学家欧拉(L. Euler,1707—1783)、德摩根(A. De Morgan,1806—1871)、狄利克雷(L. Dirichlet,1805—1859)对函数概念的界定以及中国数学家李善兰(1811—1882)的函数译名.在课例“正弦定理”[22]中,学生既欣赏韦达外接圆方法的精彩,也领略中国数学家梅文鼎(1633—1721)同径法的美妙.课例“二项式定理”[31]通过微视频呈现二项式定理的相关历史,东方的“贾宪三角”和西方的“帕斯卡三角”交相辉映.在课例“导数的几何意义”[32]中,教师以圆为载体,借助刘徽的“割圆术”,引导学生经历从古希腊欧几里得(Euclid,约公元前325—公元前265)、阿波罗尼斯(Apollonius,公元前3世纪)等数学家对切线的静态定义,逐渐过渡到17世纪费马(P. de Fermat,1601—1665)、笛卡儿(R. Descartes,1596—1690)等数学家对切线的动态定义,进而探究切线与导数几何意义之间的联系,感悟以直代曲的数学思想方法.
在上述课例中,仿佛东西方数学家穿越时空,齐聚今日课堂,探讨数学概念的起源和定义、数学定理的发现和证明,体现了精彩纷呈的多元文化.
5 讨论
表4给出了20个HPM课例[14–33]在数学文化五维度上的分布情况.
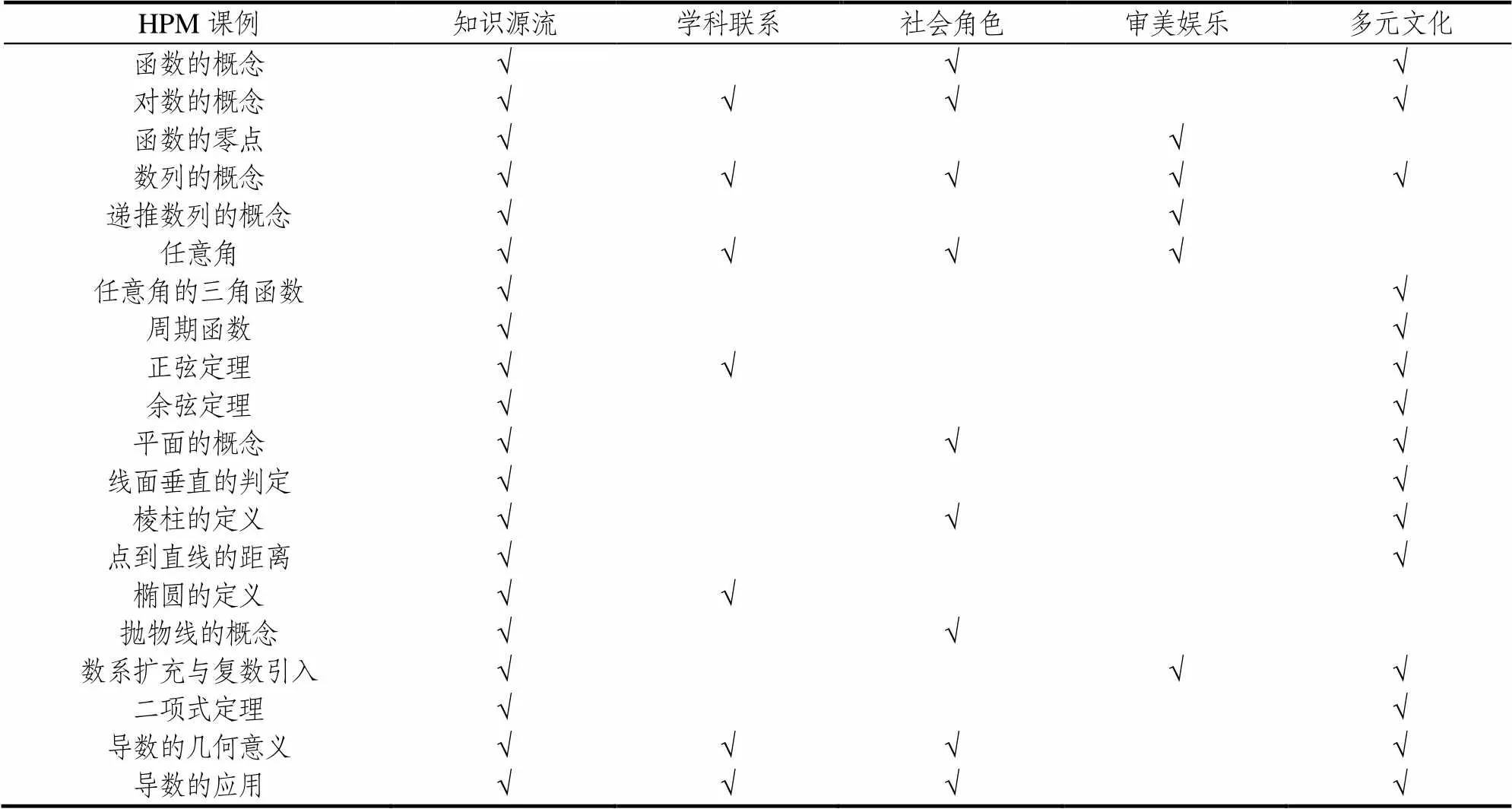
表4 数学文化各维度的课例分布情况
由表4可知,20个HPM课例中在数学文化内涵的5个维度上分布不均衡.数学文化内涵各维度及其课例个数为:“知识源流”20个、“多元文化”15个、“社会角色”9个、“学科联系”7个、“审美娱乐”5个.
首先,HPM视角下的数学教学在历史与现实之间架起一座桥梁,借鉴知识的历史发展规律,实现历史顺序、逻辑顺序和心理顺序的统一,突出HPM教学的基本特征.因此,所有HPM课例均体现了“知识源流”维度.其次,数学文化是不同时空下古今中外的数学交汇和文化碰撞,不同文化背景的数学家皆可能做出各自的贡献(如符号的创造、公式的推导、定理的证明等).因此,当教师将数学史融入教学时常常会涉及“多元文化”维度,这是该维度出现的频数仅次于“知识源流”维度频数的主要原因.此外,含有“社会角色”“学科联系”“审美娱乐”维度的课例个数呈现递减趋势,可见这3个维度的运用情况不够理想,有待继续加强.
尽管部分课例采用了HPM视角,但其“文化味”仍显不足.究其原因,主要有3个因素制约了数学文化的多元运用.
(1)教师在数学文化内涵理解上的局限性.数学史是数学文化的重要组成部分,在一定程度上,数学史融入数学教学可以视为数学文化融入数学教学的一种途径.但HPM专业学习共同体对于“基于数学史的数学文化”的内涵并无清晰的界定与分类,因而在选择和运用史料时忽视了某些维度.
(2)教师可支配的数学文化素材比较单一.以“数系的扩充与复数的引入”[30]为例,通过了解数学家(如莱布尼兹、爱因斯坦)对虚数的评价,点明发现虚数的重要性.除此之外,历史上还有一些文学名著,如扎米亚金(Y. Zamyatin,1884—1937)在《我们》中、穆西尔(R. Musil,1880—1942)在《小特尔莱斯》中用虚数来比喻人性中的非理性一面,表明作家对虚数的错误认识;美国电气工程师斯坦梅茨(C. P. Steinmetz,1865—1923)将虚数用于电路计算,体现了虚数的多元价值.这样,“学科联系”维度便得到了充分展现.
(3)数学教学现实条件的制约.许多HPM课例是在常规课堂上实施的,教师既要完成一定的教学目标,保证高考制度下的应用练习时间,又要兼顾班级的教学进度.因此,在实际教学中,不能苛求一节课体现出数学文化的所有维度,其所承载的历史素材宜少不宜多、宜精不宜杂.
6 结语
随着《标准》中“数学文化”概念的明确提出,高中数学文化研究逐渐成为数学教育领域的热点话题.张奠宙先生在谈及“如何在数学课堂教学中呈现与揭示数学文化”时,曾指出:如果数学课堂能够有广博的文化知识滋养,充满高雅的文化氛围,弥漫着优秀的文化传统,数学教学可以说达到最高境界了[34].
综上,在分析的HPM课例中,“基于数学史的数学文化”内涵的5个维度——知识源流、学科联系、社会角色、多元文化和审美娱乐均有体现,基本检验了“基于数学史的数学文化”内涵分析框架的客观合理性.然而,5个维度的分布不均,值得后续深入研究与改善.要在高中数学常态课中更加全面地呈现数学文化内涵的5个维度,进一步提升数学教学的人文氛围,HPM学习共同体需要做好如下4个方面的研究工作.
(1)注重历史学习.HPM教学的“文化之魅”始于数学史研究,数学史蕴含着丰富的教学素材和思想养料.所谓有源之水常新,有根之木常青,加强教育取向的数学史学习是未来HPM课例中数学文化内涵多元维度开发的基础环节.
(2)夯实理论基础.HPM研究基于“自下而上”的研究取径,基于教学实践的HPM课例检验了“基于数学史的数学文化”内涵分析框架的客观合理性.同时,该分析框架也可以反过来指导HPM教学实践.未来,需要基于更多的一线教学实践经验,不断对“基于数学史的数学文化”内涵开展更加深刻地研究.
(3)立足教育现实.数学文化融入数学教学,其最终目的是促进学生的数学学习,为未来发展打下良好的基础.可见,HPM视角下的数学教学不可能脱离教育现实来进行,任何一位一线教师都不可能仅为文化而文化,为历史而历史.因此,数学教师可以根据实际学情,借助“基于数学史的数学文化”内涵分析框架来创设蕴含数学文化的学习情境,编制数学文化的相关习题.同时,随着“互联网+教育”的发展,可以基于该分析框架来制作短小精炼、生动有趣的HPM微视频,助力一线数学教学.
(4)加强实证研究.“基于数学史的数学文化”内涵分析框架的实证研究有助于在数学教学中落实数学学科“立德树人”根本任务.未来,数学史融入数学教学实践,需要进一步提升质性研究与量化研究相结合的实证研究,更加深刻地揭示数学文化的教育价值.
美国学者Bidwell曾说过:在教学中融入数学史,可以将学生从数学的孤岛上挽救出来,并将他们安置于一个生机勃勃的新大陆上,这个新大陆包含了开放的、生动活泼的、充满人情味的并且总是饶有趣味的数学[35].随着HPM理论研究与教学实践的深入,充满文化芬芳的数学课堂必将彰显“立德树人”的教育价值,焕发更加强大的生命力.
[1] 顾沛.南开大学的数学文化课程十年来的探索与实践——兼谈科学教育与人文教育的融合[J].中国高教研究,2011(9):92–94.
[2] 代钦.释数学文化[J].数学通报,2013,52(4):1–4.
[3] 杨豫晖,吴姣,宋乃庆.中国数学文化研究述评[J].数学教育学报,2015,24(1):87–90.
[4] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:8–34,69,82–83.
[5] WANG X, QI C, WANG K. A categorization model for educational values of history of mathematics: An empirical study [J]. Science & Education, 2017 (26): 1 029–1 052.
[6] 张奠宙.关于数学史和数学文化[J].高等数学研究,2008(1):18–22.
[7] 高媛,陆奥帆,魏雪峰,等.德尔菲法及其在中国地平线项目中的应用[J].中国远程教育,2018(5):9–14.
[8] KUCKARTZ U. Qualitative text analysis: A guide to methods, practice and using software [M]. London: SAGE, 2014: 62–118.
[9] 汪晓勤.HPM:数学史与数学教育[M].北京:科学出版社,2017:422–425.
[10] 汪晓勤.基于数学史的数学文化内涵课例分析[J].上海课程教学研究,2019(2):37–43.
[11] TZANAKIS C, ARCAVI A. Integrating history of mathematics in the classroom: An analytic survey [M] // FAUVEL J, van MAANEN J. History in mathematics education. Dordrecht: Kluwer Academic Publishers, 2000: 201–240.
[12] FAUVEL J. Using history in mathematics education [J]. For the Learning of Mathematics, 1991, 11 (2): 3–6.
[13] JANKVIST U T. A categorization of the “whys” and “hows” of using history in mathematics education [J]. Educational Studies in Mathematics, 2009, 71 (3): 235–261.
[14] 钟萍,汪晓勤.函数概念:基于历史相似性自然过渡[J].教育研究与评论(中学教育教学版),2016(2):62–68.
[15] 钟萍,汪晓勤.对数概念:从历史到课堂[J].中学数学月刊,2015(5):50–53.
[16] 陈飞.“函数的零点”:用历史故事和问题激发动机[J].教育研究与评论(中学教育教学版),2015(12):28–31.
[17] 李玲,汪晓勤.数列概念:通过历史体现“奇、趣、本、用”[J].教育研究与评论(中学教育教学版),2016(4):61–65.
[18] 李玲.“递推数列”:从汉诺塔游戏出发[J].教育研究与评论(中学教育教学版),2015(9):19–23.
[19] 饶彬.“任意角”:从历史看必要性与规定[J].教育研究与评论(中学教育教学版),2017(4):45–51.
[20] 刘石洋.HPM视角下的“任意角的三角函数”教学[J].教育研究与评论(中学教育教学版),2014(12):33–37.
[21] 向荣,陈莎莎,沈中宇.HPM视角下的周期函数概念教学[J].中小学数学(高中版),2018(11):45–50.
[22] 张筱瑜,汪晓勤.“正弦定理”:用历史拓思维、润情感[J].教育研究与评论(中学教育教学版),2015(6):21–25.
[23] 顾彦琼,汪晓勤.“余弦定理”复习课:通过数学史体现综合性[J].教育研究与评论(中学教育教学版),2015(2):52–57.
[24] 沈中宇,汪晓勤.平面概念:基于相似性,重构数学史[J].教育研究与评论(中学教育教学版),2016(10):46–51.
[25] 高振严,何伟淋.“线面垂直判定定理”:从历史看证明、找模型[J].教育研究与评论(中学教育教学版),2018(7):35–40.
[26] 陈锋.基于历史相似性的棱柱定义教学[J].教育研究与评论(中学教育教学版),2015(5):52–57.
[27] 杨懿荔,汪晓勤.“点到直线的距离”:基于认识基础,选择历史方法[J].教育研究与评论(中学教育教学版),2017(2):60–64.
[28] 陈锋,王芳.基于旦德林双球模型的椭圆定义教学[J].数学教学,2012(4):5–8.
[29] 徐超.抛物线概念教学:重构数学史[J].教育研究与评论(中学教育教学版),2015(8):26–31.
[30] 方国青,王芳.HPM视角下“数系的扩充与复数的引入”课例研究[J].数学教学,2013(4):29–32.
[31] 方倩.“二项式定理”:在历史中探源、求法、寻魅[J].教育研究与评论(中学教育教学版),2016(9):37–41.
[32] 王芳,汪晓勤.HPM视角下“导数几何意义”的教学[J].数学教育学报,2012,21(5):57–60.
[33] 王芳,汪晓勤.HPM视角下的“导数应用”教学[J].数学通报,2014,53(9):28–32.
[34] 张奠宙.数学教育纵横[M].南宁:广西教育出版社,2018:378–379.
[35] BIDWELL J K. Humanize your classroom with the history of mathematics [J]. Mathematics Teacher, 1993, 86 (6): 461–464.
An Empirical Study of the Meaning of Mathematical Culture Based on the History of Mathematics
YU Qing-chun1, WANG Xiao-qin2
(1. School of Mathematical Science, East China Normal University, Shanghai 200241, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China)
Employing the Delphi method and content analysis, this study carried out qualitative research on demonstrating and revising the analytical framework of mathematical culture based on the history of mathematics and analyzed 20 lessons using history of mathematics (HPM) lessons in senior high school from 2012 to 2018. We found that the meaning of mathematical culture based on the history of mathematics can be divided into five dimensions: knowledge of origin, connection of disciplines, role in society, entertainment of aesthetics, and multiculturalism. However, these five dimensions are unevenly applied in teaching practice. To reveal the value of mathematics culture in teaching, teachers need to pay attention to the history of mathematics, consolidate their theoretical basis, teach based on educational reality, and promote empirical research.
Delphi method; text analysis; history of mathematics; mathematical culture; HPM lesson
G40–055
A
1004–9894(2020)03–0068–07
2020–01–20
上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究(A8)
余庆纯(1993—),女,广东潮州人,博士生,主要从事数学史与数学教育研究.
余庆纯,汪晓勤.基于数学史的数学文化内涵实证研究[J].数学教育学报,2020,29(3):68-74.
[责任编校:周学智、陈隽]
