儿童近似数量系统精确性与数学能力的关系研究

康 丹，张 利，蔡 术，刘江萍，陆梅怡，刘秋香

儿童近似数量系统精确性与数学能力的关系研究

康 丹，张 利，蔡 术，刘江萍，陆梅怡，刘秋香

（湖南师范大学 教育科学学院 认知与人类行为实验室，湖南 长沙 410081）

近似数量系统是儿童数学能力发展的基础．已有研究表明：近似数量系统可以预测儿童的数学能力；两者关系的中介变量可能是执行功能、视觉空间能力及基数概念等；近似数量表征能力可以通过训练得到改善．未来的研究还需要进一步标准化儿童近似数量系统的测量工具；借助认知神经科学进一步厘清近似数量系统与数学能力关系的内在机制；提供更可靠的证据证明近似数量系统训练的价值和长期效应．建议：要重视ANS精确性对儿童数学能力发展的价值；早期儿童的数学教育中可以渗透执行功能、视觉空间能力等认知能力的训练；借鉴或改进已有的ANS训练范式，提升儿童的ANS精确性和数学能力．

近似数量系统；执行功能；数学能力

儿童早期数学能力的发展与未来的社会地位和经济水平密切相关．数学能力的发展表现出一定的稳定性，学前阶段儿童的数感能预测小学一年级、三年级、五年级、八年级甚至高中的数学成绩[1]．儿童数学能力在早期就表现出较大的个体差异，这种差异会一直延续到学龄期．造成这种个体差异的因素至少有两个．一个是个体长期接受正式数学学习而获得的经验；另一个则是个体在接受正式数学教学前就具有的直观的、非言语性的近似数感[2]，Halberda和Feigenson将其称为近似数量系统（approximate number system，简称ANS），包括非符号性的近似数量系统和符号性近似数量系统．它具有遗传性和不精确性，是一种运用近似数量的方式来表征数量的非言语能力．这种数感不仅跨越物种，而且在个体整个生命周期中都保持活跃．神经科学研究表明，近似数量系统有其相应的脑区定位，位于大脑顶内沟（bilateral intraparietal sulcus，IPS）[3]．作为一种与生俱来的结构，相较于一般认知能力，近似数量系统更可能是儿童高级数学能力发展的基础．而且，近似数量表征的模块和类别是理解数和数学认知的来源的核心问题．对近似数量系统进行深入研究并分析其与数学能力的关系，既可以进一步解释数学能力个体差异的缘由，也对研究人类数学能力发展的起源有重要的启示．

研究主要分析以下几个问题：儿童近似数量系统的表征与测量方式有哪些？儿童近似数量系统与数学能力之间是否是线性关系？如果不是，它们之间的中介变量有哪些？对儿童近似数量系统的训练方案有哪些？效果如何？

1 文献检索词和检索策略

以“近似数量系统”“数学能力”为主题词，在中国知网资源总库中进行检索，筛选了16篇较高质量的论文．以相同的方法检索万方数据库，筛选出文献12篇．从两个中文数据库筛选的文章大部分是重叠的．以英文关键词“approximate number system”和“mathematical ability”为基本条件，限定发表时间为近20年，检索Web of Science、PubMed、SpringerLink、ProQuest和 American Psychological Association等数据库，共搜索出82篇．通过标题和摘要进一步选取符合研究主题的文献，纳入文献标准如下：以3~16岁学生为研究对象，涉及近似数量系统的表征、测量、训练、与数学能力的关系的研究；具有代表性的文献综述和重要实证研究．最终确定49篇文献．

2 ANS精确性的表征及测量

ANS的数量表征是在心理数字线（mental number line）上的一系列类似高斯调谐曲线，每个数量表征的标准差反映了“噪音”的大小，即与需表征的数量不相干的错误信息[4]，如图1所示．ANS以不精确的方式表征数字，其数值估计的不精确性随着目标数量的增加而增长．但个体内部表征的过程中会出现与数量不相关的错误信息，也就是“噪音”[5]，噪音越大，错误信息越多，该系统对数量的表征就越不精确．个体ANS噪音量通常用韦伯分数（W）来表示，对数量的区分遵循韦伯定律（Weber’s law），即个体对数量的区分依赖于它们之间的比率，而不是它们之间的绝对差异．韦伯分数等于两个数字之间的差除以较小的数字[6]．若两个数的数量比率越大，则判断反应时越短，正确率越高；若比率相等，数量值越大则反应时越长，正确率越低，这就是数大小效应和数距离效应[7]．因此，有的研究将数大小和数距离效应作为判断ANS精确性的依据．

对儿童和成年人进行ANS测量的方式主要有3种：符号数量比较任务、非符号数量比较任务和近似加法比较任务．符号数量比较任务与非符号数量比较任务的测查程序相同，都是在电脑上呈现视觉刺激，前者是两个阿拉伯数字，后者则是两个点阵，让被试判断出数字或点集合较大/多的组．近似加法比较任务对于低龄儿童难度较大，该任务先呈现一个集合，随后该集合隐藏在一个容器中（如箱子），紧接着第二个集合也隐藏于这个容器中，最后呈现的第三个集合隐藏在第二个容器中．要求被试判断两个容器中哪个容器中包含的物体更多．这3种测量方式均以数量比较的正确率、反应时或韦伯分数作为判断ANS精确性的指标．其中，非符号数量比较任务相比其他两项任务具有更好的可行性以及信度[9]．该任务的难度由两组点数集合的比率来控制，数字比率越接近于1，数量辨别难度性越大[10]．例如，区分8个点和10个点（比率为0.8）比8个点和16个点（比率为0.5）更难．

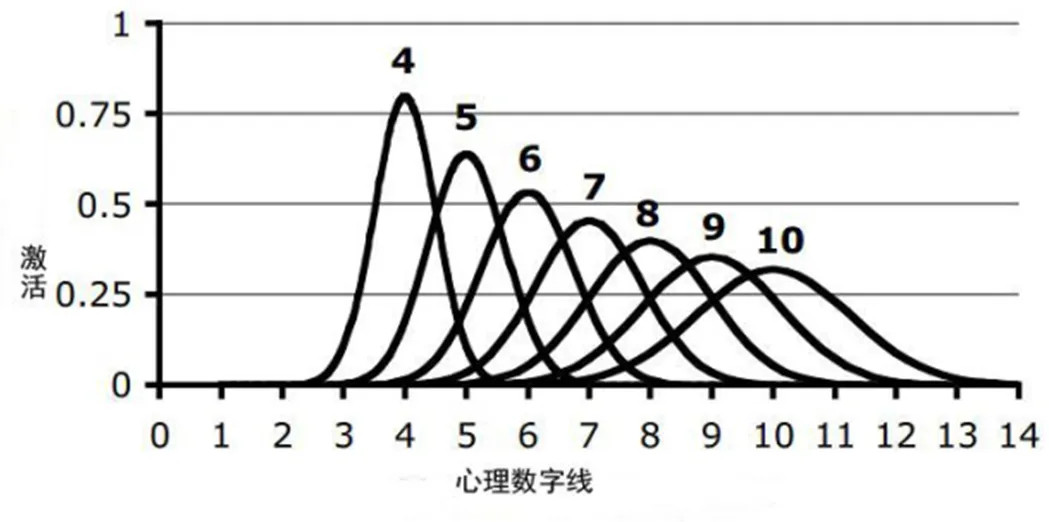
图1 近似数量系统对数量的表征形式[8]

3 ANS精确性与数学能力的关系

根据数学特定领域技能可以将数学能力划分为符号数学能力和非符号数学能力．符号数学能力特指与数学符号（阿拉伯数字或文字）有关的数学认知能力，是人类所独有的，这种能力使得人们可以进行精确的数运算，如计数，基数和数字识别；非符号数学能力指的是与符号表征无关的直觉性或口头性的数学能力，如唱数、比较数的大小[11]．

ANS与大脑特定的神经区域顶内沟相关联，并能激活顶叶和额叶皮质参与活动[12]．顶内沟也是数学的重要活跃区，它专门运算数值和进行数学思维[13]，此外，临近大脑皮层表面的额叶和顶叶区域都与数学能力的发展有关[14]．综合近似数量系统与数学能力发展的脑机制研究，它们与顶内沟、顶叶与额叶皮质相关联，为更进一步地探究两者关系提供了有力证据．

3.1 ANS精确性可以预测儿童的数学能力

考察ANS精确性与数学能力关系的研究近十年来逐渐增多，已有多项纵向研究表明，ANS精确性可以预测儿童的数学能力．在控制了一般智力因素后，6个月的婴儿对数量的偏好可以预测3年后的标准化数学能力测验得分[15]．对3~6岁儿童的研究中，控制了年龄、表达性词汇、早期数学能力等潜在因素的影响后，ANS精确性对儿童两年后的数学能力仍有显著的预测作用[16]．研究者对学龄儿童的研究得到了相似的结论，控制言语智商、执行功能等众多因素后，14岁时的韦伯分数可以回溯预测5岁时数学标准化测验的得分[17]；四、六年级的小学生的近似数量表征能力对两个年级学生的数学成绩均有一定的预测作用[18]．以上研究结果表明，学前儿童和学龄儿童的ANS精确性可以预测数学能力，但这些结果并不一定说明二者之间是因果关系．未来评估ANS精确性与数学能力之间是否具有因果关系，还需要更加严格的实验设计．第一，设计旨在提高儿童ANS精确性的训练措施，但不影响其他因素，再探讨儿童的数学能力是否因为训练得到提高；第二，随机分配被试，并在干预前后评估儿童的数学能力发展现状．

近年来，研究者将研究的视角进一步精细到关注ANS精确性与符号数学能力的关系．Wang等研究者对13~16岁青少年的研究发现，ANS精确性与两个常用标准化考试（SAT和ACT）的符号数学部分的成绩显著相关[19]，即使控制了年龄、言语表现和反应时间，这种相关关系也是稳定的．但在学前阶段，ANS精确性与数学能力的关系更密切．Purpura和Logan在学期的开始和结束时分别对3~5岁儿童的ANS精确性、数学语言和早期符号数学能力等一系列认知技能进行了评估，其中，ANS精确性预测了符号数学能力的发展，并能解释数学成绩变异的25%[20]．这些研究说明，在早期的数学学习中，先天性的ANS对个体数学符号的学习很关键．其原因在于儿童开始学习阿拉伯数字时，需要将特定的数字符号与其近似表征相匹配，这种数和符号的对应是儿童获取数字符号意义的基础．从种系发生学角度看，ANS虽是人类与其它生物共享的先天进化基础，但拥有符号系统和语言系统是人类和其他物种的区别．动物进化出近似表征能力止于物种的生存和繁衍，人类则借助这种先天的数量表征能力进一步发展数学能力．可以说，ANS是人类的符号数学能力的认知基础．

那么，ANS精确性与数学能力的关系是呈现线性的吗？研究发现，ANS精确性与数学能力并非线性关系[21]．数学能力低的儿童与数学能力高的儿童相比，前者ANS精确性与数学能力的关系更密切[22]．而且，执行功能、视觉空间能力、基数概念等都可能在ANS精确性与数学能力的关系中起作用．

3.2 ANS精确性与数学能力关系的中介变量

Moore等人发现，ANS是通过众多领域特殊性技能（如基数概念）和领域一般性技能（视觉空间能力、执行功能）对儿童数学能力产生影响的[23]．这说明了ANS与数学能力之间可能存在一系列的中介变量．

3.2.1 执行功能

执行功能是个体对意识和行为的自我调节和以明确目标为导向的活动过程，包括抑制控制、认知灵活性和工作记忆[24]．抑制控制（inhibitory contorl）指个体在认知活动中对无关刺激做出抑制反应的能力；工作记忆（working memory）是指大脑在短时间内存储信息，并对信息进行刷新或运算；认知灵活性（cognitive Flexibility）需建立在规则基础上，在不同任务或心理定势间灵活转换注意力，是克服心理定势的影响并保持思维和动作灵活性的过程．

ANS和数学能力之间的联系可以通过执行功能来解释．执行功能已被证明是儿童数学学习的重要认知加工机制，其3种核心成分也是数学能力的重要预测指标[25-27]．认知神经科学的研究表明，ANS、执行功能、数学能力有重叠的生理结构——额叶和顶叶，可为3者的关系研究提供有力依据．在儿童进行近似数量表征时，受到执行功能的制约．工作记忆的容量是儿童近似表征的基础，外部输入的数值信息均需要进入工作记忆储存，一旦数值信息和其他干扰信息在竞争工作记忆的空间，儿童近似数量表征的难度就会增大．此时抑制控制和认知灵活性就显得尤为重要，抑制控制能防止无关信息进入并将有效信息保持在工作记忆中以保障认知过程的完整，认知灵活性则能灵活转换注意力并集中于认知目标上，维持ANS的有效运作．已有研究也表明，抑制控制和工作记忆可在ANS精确性和数学能力的关系中起部分中介作用[28]．此外，根据映射理论，在学龄前，儿童就表现出将非符号数量映射到心理数字线上的能力，数量的空间映射可能是儿童理解数字间的大小关系的关键[29]．对于大数量的近似表征，个体也需要借助认知灵活性来完成不同的心理数字线区间的数量——数字映射，认知灵活性或许能进一步解释ANS精确性与数学能力的关系．总体上来讲，还需要进一步的研究来证实在不同年龄阶段工作记忆、抑制控制、认知灵活性是否存在中介作用．

3.2.2 视觉空间能力

视觉空间能力对于需要以较低水平的视觉感知为基础的ANS非常重要[30]，这种能力似乎是感知4以上大数量以及符号数学的关键组成部分．一项对808名三~五年级的儿童（包括数学学习困难的儿童）的研究表明，困难儿童的几何图形辨别能力和ANS精确性都与算术技能相关，同时数困儿童与非数困儿童的几何图形辨别的差异与ANS精确性的差异有关[31]．这表明，视觉空间能力可能对于儿童算术能力和ANS精确性都非常重要，并且算术能力和ANS精确性有紧密的联系．Zhou及其同事认为，视觉空间能力可以解释ANS精确性与算术之间的密切关系．他们发现，在控制视觉空间能力分数（包括图形匹配、心理旋转和视觉追踪）等无关变量后，三~五年级儿童的ANS精确性与精确计算之间不存在相关关系，但视觉空间能力仍然可以预测算术水平，视觉空间能力是两者之间的重要中介变量[21]．由此可见，尽管ANS精确性对算术水平有相应的影响，但两者关系不是线性或因果关系，ANS是通过视觉空间能力来影响算术技能的．

3.2.3 基数概念

基数概念是表征任意集合所含元素数量多少的概念．基数概念的发展使儿童在具体的实物和抽象的数概念之间建立联系．早期的ANS可以帮助儿童学习基数概念．儿童最初学习符号数学时需要借助ANS明确该符号在心理数字线上的位置，在明确了具体的数学符号的意义后，儿童才可以独立于ANS学习高阶的数学知识．按照这一逻辑，儿童早期的基数概念可能是联结ANS精确性和数学能力之间的桥梁．这一观点也得到了相关研究的支持．例如，Chu等人在评估学前儿童ANS精确性、基数概念和数学能力的关系时，他们发现，无论是否控制执行功能、智力、父母受教育程度等因素，3~4岁儿童入学前的ANS精确性和基数概念都是学期末数学能力的重要预测因素，进一步数据分析表明基数概念是ANS精确性与数学能力的中介变量[32]．Peng等人也以学前儿童为研究对象调查了基数概念的中介效应，在控制无关变量后，基数概念对ANS精确性与算术的关系表现出中等中介效应[33]．这一研究结果与Lyons等人在2011年以成年人为研究对象的结论是一致的[34]．这可能是ANS可以促进人类对基数概念的理解，并间接影响其它方面的数学学习，甚至影响到未来高阶数学能力的发展．

ANS精确性与数学能力不是线性相关的观点已得到众多研究的支持，未来研究可以深入探讨以明确ANS与数学能力之间相互作用的内在机制．鉴于ANS对早期数学能力尤其是符号数学能力的影响，已有研究针对ANS设计了训练方案并具有良好的训练效果．

4 对ANS精确性的训练研究

ANS具有可塑性，可以通过训练来改善，特别是对低收入家庭的数学学习困难儿童而言，适宜的训练可显著提高他们的数学能力．ANS精确性容易受到经验和环境的影响，个体从婴儿期到成人期，ANS精确性一直呈上升趋势直到30岁左右才达到顶峰[35]．已有文献中涉及到ANS的训练方案主要有两种类型，一种是非符号近似数量系统训练，另一种是符号近似数量系统训练．

4.1 非符号近似数量系统训练

学前儿童和成人可以通过短期的近似算术训练（approximate arithmetic training，简称AAT）提高近似数量表征能力和符号数学能力．Park和Brannon基于ANS的表征特点开发了非符号的近似加减法的训练任务，对大学生的训练结果显示，AAT有效的提高了大学生的算术技能，这一研究也发现了ANS与符号数学能力之间可能存在潜在的因果关系[36]．但由于AAT中涉及加减法，这种训练可能已经超出了ANS自身的工作范围．因此，Park和Brannon在此实验基础上进一步改善实验，排除了如视觉工作记忆、AAT训练期间隐藏的符号性算术技能、安慰剂效应等影响，AAT训练组的符号数学能力仍显著提高[37]，这说明ANS对符号数学能力可能有特殊的迁移作用．这项任务对提高低收入家庭的学前儿童的数学入学水平也有显著效果[38]．后来，Jacky在AAT的设计原理基础上进一步强化了非符号刺激训练，对57名18~35岁的成年人进行为期一周的训练，在控制了语言差异后，AAT实验组与对照组相比，实验组ANS数量距离效应变小精确性增加，而且算术的精确度也有所提高[39]．AAT的训练研究说明，符号数学能力和非符号数学能力可能有共同认知基础[40]，AAT任务提高ANS近似算术技能的同时，也提高了符号数学能力（算术技能）．另外，AAT任务为未来的研究提供了探究潜在机制的途径——借助AAT研究ANS精确性和算术技能对数学能力的贡献．

另外，van Herwegen运用感官刺激开发了一个学前儿童数学学习系统（the preschool number learning scheme，简称PLUS），这个项目也是用来训练儿童的非符号近似数量系统，目的在于提升学前儿童的ANS精确性．PLUS采用的是学龄前儿童熟悉的游戏（演奏乐器、玩多米诺骨牌游戏）和两种与ANS相关的游戏（估算、匹配大数字）．所有的游戏都从大比率1∶2开始，游戏呈现的数量比率随着时间的推移越来越小，难度逐渐增大．结果表明，5周后，与阅读组（控制组）相比实验组表现出较好的ANS精确性，可见为期5周每天10分钟的PLUS提高了学前儿童的ANS精确性[41]．

4.2 符号近似数量系统训练

为了探究非符号训练和符号训练哪种方法对数学学习困难的儿童更有效，Van Herwegen等人2018年设计了符号性的数字游戏（Digit Game）任务提升儿童的符号数学能力，与非符号性的PULS游戏进行比较．这个任务将学前儿童熟悉的加法和数字游戏分别改编为计数和数字匹配游戏．训练频率是为期5周每周两次10分钟的训练．结果显示，两个训练项目都提高了ANS精确性和早期数学能力并具有长期效应[42]．数学学习困难儿童的数学能力发展缺陷往往能追溯到学前教育阶段，学前阶段就应该重视以游戏的方式渗透符号和非符号数学能力的培养，使数学能力差的儿童受益，这在一定程度上能够预防未来的数学学习困难．

另外，Honoré和Noël也开发了基于ANS的符号或非符号比较训练（Symbolic training，Non-symbolic training），并比较了它们对学前儿童算术技能的影响．他们将56名5~6岁儿童随机分成3组：非符号ANS训练、符号ANS训练、故事理解训练，并进行实验前后测试．每周训练一次，一次30分钟，共10周．结果显示，两种训练计划都能有效提高ANS符号估计和非符号估计的精确性，但符号ANS训练比非符号ANS训练更能提高儿童的算术技能[43]．这项研究说明符号数学对算术技能的影响更大，同时研究进一步证明了非符号数学能力可以影响符号数学能力，这或许是因为符号数学通过非符号（如“点集合”）赋予符号以具体意义，并通过从非符号到符号的映射来调节符号系统．

以上这些ANS的训练主要集中在学前期进行，并且具有良好的训练效果．从4岁到小学一年级是儿童数学认知和能力增长的重要时期，这时针对儿童ANS精确性设计的游戏或训练方案能够改善他们的近似数量表征水平和数学能力，对其日后符号数学能力甚至更高层次的数学学习能力的发展都具有长远意义．然而，现有训练研究还没有考虑中介因素，如在训练方案融入执行功能、基数概念等因素，也没有研究证实训练ANS还是训练中介因素更能提高儿童的近似数量表征能力和数学能力．还需要从环境因素和个体认知因素两方面深入探究影响ANS与数学能力关系的适当训练因素，采用严谨的实验设计进行对比研究；现有研究中，还没能针对不同年龄段的儿童设计出相应的训练方案，还需要根据不同年龄儿童的ANS和数学能力的发展特点、学习方式等进行整体设计．

5 研究展望与教育建议

5.1 研究展望

近20年来国外出现了大量对ANS的研究文献，国内相关研究还比较少，近几年来相关研究出现了迅速增加的趋势．对ANS的研究已经成为一个热点问题．已有的研究关注了近似数量系统的发展特点、与数学能力的关系及可能的中介效应、训练方法等，这些研究为认识ANS打下一个坚实的基础，同时也为儿童数学教育提供了借鉴意义．结合当前数学领域研究的趋势，未来对ANS的研究还可以从以下3个方面进一步完善．

一是明确不同ANS测量工具的适宜年龄阶段．首先，目前常用的测量任务是非符号数量比较任务、近似加法比较任务、符号数量比较任务，但在已有研究中使用这3种测量任务得到的ANS的结果并不一定相关的．例如，成人的非符号数量比较任务和近似加法任务的得分不相关，而在5~11岁儿童中，两个任务的得分存在中等程度相关[44]．这些矛盾说明不同的ANS测量任务可能适用于不同的年龄阶段．其次，现有的测量工具应该针对不同年段的研究对象的特点进行优化，如非符号数量比较任务采用计算机呈现刺激，儿童通过按键盘上的按键进行选择，对于学前儿童而言，该任务有些枯燥无趣，对儿童的手指灵活性也有一定的要求，不适合精细动作发展不太完善的学前儿童．为此，ANS测量工具的开发或改进应该考虑研究对象的年龄特征，结合ANS发挥作用的大脑机制明确测量任务适用的年龄阶段及相应的数量比率、呈现时间，以提高信效度．

二是探讨ANS精确性与数学能力之间关系的内在机制．一方面，探究ANS精确性与数学能力各个维度间的相互关系，从认知神经科学的角度进一步厘清ANS影响数学能力发展的机制甚至细化到数学能力各维度上；另一方面，从发展性研究的角度，明确ANS精确性发展的关键期，进一步研究不同年龄的儿童ANS精确性与数学能力之间是否存在不同的中介效应，并分析中介变量之间有何种关联，以及中介变量是否存在发展性变化．

三是验证ANS训练的适宜性及其长期效应．在研究设计上，采用因果关系设计探究ANS精确性与数学能力之间的关系，在此基础上改进训练方法，根据不同年龄的儿童、不同类型的儿童（如数学学习困难儿童）设计符合其身心发展特点的方案，并检验方案的长期效应．未来的研究应多关注训练方案的适宜性，从认知神经科学的角度探究该训练方案之所以引起数学能力变化的内在机制，以及检验训练的长期效应，促进儿童的ANS精确性或数学能力发展．

5.2 教育建议

近似数量系统是人类数字核心系统的重要组成部分，它与精确数量系统共同解释了人类的基本数感．《数学课程标准（2011年版）》提到了10个数学核心概念，其中“数感”被摆在了首位，并明确指出：“建立数感有助于学生理解现实生活中数的意义，理解或表述具体情境中的数量关系．”这充分表明了帮助学生在数学学习过程中建立数感是课程标准十分强调和重视的问题．为此，教育者应注意以下3个方面．

首先，教育者要重视ANS精确性对儿童数学能力发展的价值．学前及小学低年级阶段是ANS精确性迅速发展的时期，在这一阶段重视儿童的数量表征，对儿童日后数学能力的发展具有重要意义．教育者应在学前和低年级数学课程中融入ANS精确性的内容，为儿童近似估计能力的发展提供支架．例如，在学前儿童的生活情景下结合实际多用“更多”“更少”或“长一些”“短一些”等表示近似量的词语与他们进行数学语言的沟通，引导他们判断一个物体或事件的量的大小，如距离、长度、持续时间、数、饱和度、亮度或其它量．在小学低年级阶段，教育者可运用实践教学法帮助儿童亲历近似表征的过程，在对比和活动中体验数感，在估算和解决问题中增强数感．这些方式都可能会加强儿童的近似数量表征能力，为儿童自然运用近似数量系统奠定基础．

其次，早期儿童的数学教育中可以渗透执行功能、视觉空间能力等一般认知能力的训练．学前期和小学低年级阶段的儿童是数感培养的最佳时期。这个阶段教师充分把握时机，在数的比较、数字的认识、数量关系或数的估算等知识的教学中，逐步提高和发展儿童的数感，为儿童数学核心素养的培养奠定坚实的基础．如果能够可以引领儿童联系自己身边具体、有趣的事物融入到儿童的数学学习，在教学设计中运用观察、计划、描述、空间记忆、解决问题等方法，既能培养儿童的执行功能和视觉空间等一般认知能力，也发展了儿童的数感．

最后，教育者可以借鉴或改进已有的ANS训练范式，提升数学学习困难儿童的ANS精确性和数学能力．机会公平是实现教育公平的关键，尤其是处于“弱势地位”的儿童也应有公平发展的机会．应该进一步关注早期数学学习困难儿童．儿童的数学学习困难一般可以追溯到早期数学能力缺陷，如ANS精确性较低，若个体从学前到小学一年级的数学学习就落后于同龄人，这种差距会随着年龄的增长继续持续扩大[45]．因此，早期对数学学习困难儿童进数学方面的训练具有非常重要的意义，可以在很大程度上提高儿童早期数学能力并降低未来数学学习失败的风险．

[1] JORDAN N C, KAPLAN D, RAMINENI C, et al. Early math matters: Kindergarten number competence and later mathematics outcomes [J]. Developmental Psychology, 2009, 45 (3): 850-867.

[2] IZARD V, SANN C, SPELKE E S, et al. Newborn infants perceive abstract numbers [J]. Proceedings of the National Academy of Sciences of the United States of America, 2009, 106 (25): 10 382-10 385.

[3] JANG S, CHO S. The mediating role of number-to-magnitude mapping precision in the relationship between approximate number sense and math achievement depends on the domain of mathematics and age [J]. Learning & Individual Differences, 2018 (64): 113-124.

[4] MAZZOCCO M M M, FEIGENSON L, HALVERDA J. Preschoolers’ precision of the approximate number system predicts later school mathematics performance [J]. Plos One, 2011, 6 (9): 1-8.

[5] 张继英．5~6岁儿童近似数量系统精确性和数学能力关系的研究[D]．上海：华东师范大学，2017：62．

[6] 杨志艳，周欣．儿童早期近似数量表征的发展与特点[J]．学前教育研究，2015（11）：44-55．

[7] 章雷钢．大、小数量表征的心理机制[D]．杭州：浙江大学，2007：76．

[8] 牛玉柏，张丽芬，肖帅，等．小学生近似数量系统敏锐度的发展趋势及其与数学能力的关系：抑制控制的中介作用[J]．心理科学，2018（2）：344-350.

[9] CHESNEY D, BJAKEBRING P, PETERS E. How to estimate how well people estimate: Evaluating measures of individual differences in the approximate number system [J]. Attention Perception & Psychophysics, 2015, 77 (8): 2 781-2 802.

[10] 牛玉柏，时冉冉，曹贤才．学前儿童近似数量系统敏锐度与符号数学能力的关系[J]．心理发展与教育，2016，32（2）：129-138.

[11]  SCHNEIDER M, BEERES K, COBAN L, et al. Associations of non-symbolic and symbolic numerical magnitude processing with mathematical competence: A meta-analysis [J]. Developmental Science, 2017, 20 (3): 572-584.

[12]  SOKOLOWSKI H M, FIAS W, MOUSA A, et al. Common and distinct brain regions in both parietal and frontal cortex support symbolic and nonsymbolic number processing in humans: A functional neuroimaging meta-analysis [J]. Neuroimage, 2017, 146 (28): 376-394.

[13]  AMALRIC M, DEHAENE S. Origins of the brain networks for advanced mathematics in expert mathematicians [J]. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113 (18): 4 909-4 914.

[14]  ARSALIDOU M, PAWLIW L M, SADEGHI M, et al. Brain areas associated with numbers and calculations in children: Meta-analyses of fMRI studies [J]. Developmental Cognitive Neuroscience, 2017, 132 (16): 1-12.

[15]  STARR A, LIBERTUS M E, BRANNON E M. Number sense in infancy predicts mathematical abilities in childhood [J]. Proceedings of the National Academy of Sciences, 2013, 110 (45): 18 116-18 120.

[16]  GOBEL S M, WATSON S E, LEVAG A, et al. Children’s arithmetic development: It is number knowledge, not the approximate number sense, that counts [J]. Psychological Science, 2014, 25 (3): 789-798.

[17]  HALBERDA J, FEIGENSON L. Developmental change in the acuity of the “number sense”: The approximate number system in 3, 4, 5, and 6-year-olds and adults [J]. Developmental Psychology, 2008, 44 (5): 1 457-1 465.

[18] 孔海燕，孙雨，宋广文．小学生近似数量表征系统和工作记忆与数学成绩的关系[J]．数学教育学报，2017，26（2）：14-18．

[19]  WANG J J, HALBERDA J, FEIGENSON L. Approximate number sense correlates with math performance in gifted adolescents [J]. Acta Psychological, 2017, 176 (38): 78-84.

[20]  PURPURA D J, Logan J A. The nonlinear relations of the approximate number system and mathematical language to early mathematics development [J]. Developmental Psychology, 2015, 51 (12): 1 717-1 724.

[21]  XINLIN Z, WEI W, YIYUN Z, et al. Visual perception can account for the close relation between numerosity processing and computational fluency [J]. Frontiers in Psychology, 2015 (6): 1 364-1 378.

[22]  BONNY J W, LOURENCO S F. The approximate number system and its relation to early math achievement: Evidence from the preschool years [J]. Journal of Experimental Child Psychology, 2013, 114 (3): 375-388.

[23]  MOORE A M, VANMARLE K, GEARY D C. Kindergartners’ fluent processing of symbolic numerical magnitude is predicted by their cardinal knowledge and implicit understanding of arithmetic two years earlier [J]. Journal of Experimental Child Psychology, 2016, 150 (56): 31-47.

[24]  MIYAKE A, FRIEDMAN N P. The nature and organization of individual differences in executive functions: Four general conclusions [J]. Current Directions in Psychological Science, 2012, 21 (1): 8-14.

[25] 康丹，李飞燕，文鑫，等．5~6岁潜在数学学习困难儿童数学和工作记忆的4周游戏训练效果[J]．中国心理卫生杂志，2018，32（6）：495-501．

[26]  RIBNER A, MOELLER K, WILLOUGHBY M, et al. Cognitive abilities and mathematical competencies at school entry [J]. Mind Brain & Education, 2017 (3): 1 026-2 037.

[27]  HARVEY H A, MILLER G E. Executive function skills, early mathematics, and vocabulary in head start preschool children [J]. Early Education & Development, 2017, 28 (3): 1-18.

[28]  PRICE G R, WILKEY E D. Cognitive mechanisms underlying the relation between nonsymbolic and symbolic magnitude processing and their relation to math [J]. Cognitive Development, 2017 (44): 139–149.

[29]  SELLA F, BERTELETTI I, LUCANGELI D, et al. Preschool children use space, rather than counting, to infer the numerical magnitude of digits: Evidence for a spatial mapping principle [J]. Cognition, 2017 (158): 56-67.

[30]  CUI J, ZHANG Y, CHENG D, et al. Visual form perception can be a cognitive correlate of lower level math categories for teenagers [J]. Frontiers in Psychology, 2017, 8 (32): 1 336-1 348.

[31]  ZHOU X, CHENG D. When and why numerosity processing is associated with developmental dyscalculia [M]. The Routledge International Handbook of Dyscalculia and Mathematical Learning Difficulties, 2014: 156-162.

[32]  CHU F W, VANMARLE K, GEARY D C. Early numerical foundations of young children’s mathematical development [J]. Journal of Experimental Child Psychology, 2015, 132 (15): 205-212.

[33]  PENG P, YANG X, MENG X. The relation between approximate number system and early arithmetic: The mediation role of numerical knowledge [J]. Journal of Experimental Child Psychology, 2017, 157 (32): 111-124.

[34]  LYONS I M, BEILOCK S L. Numerical ordering ability mediates the relation between number-sense and arithmetic competence [J]. Cognition, 2011, 121 (2): 256-261.

[35]  HALBERDA J, LY R, WILMER J B, et al. Number sense across the lifespan as revealed by a massive internet-based sample [J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109 (28): 11 116-11 120.

[36]  PARK J, BRANNON E M. Training the approximate number system improves math proficiency [J]. Psychological Science, 2013, 24 (10): 2 013-2 019.

[37] PARK J, BRANNON E M. Improving arithmetic performance with number sense training: An investigation of underlying mechanism [J]. Cognition, 2014, 133 (1): 188-200.

[38] PARK J, BERMUDEZ V, ROBERTS R C, et al. Non-symbolic approximate arithmetic training improves math performance in preschoolers [J]. Journal of Experimental Child Psychology, 2016, 152 (12): 278-284.

[39]  AU J, JAEGGI S M, Buschkuehl M. Effects of non-symbolic arithmetic training on symbolic arithmetic and the approximate number system [J]. Acta Psychologica, 2018, 185 (2): 1-12.

[40]  LUSSIER C A. Developmental bias for number words in the intraparietal sulcus [J]. Developmental Science, 2016, 20 (3): 1-18.

[41]  van J H, COSTA H M, PASSOLUNGHI M C. Improving approximate number sense abilities in preschoolers: Plus games [J]. School Psychology Quarterly, 2016, 32 (4): 428-436.

[42]  van J H, COSTA H M, NICHOLSON B, et al. Improving number abilities in low achieving preschoolers: Symbolic versus non-symbolic training programs [J]. Research in Developmental Disabilities, 2018, 77 (8): 1-11.

[43] HONORE N, NOEL M P. Improving preschoolers’ arithmetic through number magnitude training: The impact of non-symbolic and symbolic training [J]. Plos One, 2016, 11 (11): 1-22.

[44]  GILMORE C, ATTRIDGE N, SMEDT B D, et al. Measuring the approximate number system in children: Exploring the relationships among different tasks [J]. Learning & Individual Differences, 2014, 29 (1): 50-58.

[45]  MORGAN P L, FARKAS G, WU Q. Kindergarten children’s growth trajectories in reading and mathematics: Who falls increasingly behind [J]. Journal of Learning Disabilities, 2011, 44 (5): 472-488.

The Relationship between the Accuracy of Children’s Approximate Number System and Their Mathematical Ability

KANG Dan, ZHANG Li, CAI Shu, LIU Jiang-ping, LU Mei-yi, LIU Qiu-xiang

（Cognition and Human Behavior Key Laboratory of Hunan Province, College of Educational Science,Hunan Normal University, Hunan Changsha 410081, China)

The approximate number system (ANS) is regarded as the basis for the development of children’s mathematical ability. Previous studies have revealed that the ANS is a predictor of children’s mathematical ability. The mediating variables of the relationship between ANS and mathematical ability may involve executive function, visual spatial ability, and cardinal number concept. Moreover, the ability to represent approximate numbers can be improved with proper training. In future research, measurement tools for ANS should be standardized; then, the development of cognitive neuroscience may be beneficial for further elaboration of the intrinsic mechanism of the relationship between ANS accuracy and mathematical ability. Reliable evidence is needed to demonstrate the value of training with ANS and its long-term effects. We end this paper with several suggestions for educational implications of the studies. First, we should pay attention to the impact of ANS accuracy on children’s mathematical ability. Second, we need to foster the development of children’s cognitive abilities, such as executive function and visual spatial ability, in early childhood mathematical education. Third, children’s ANS accuracy and mathematical ability can be improved by refining existing ANS training programs.

approximate number system; executive function; mathematical ability

G610

A

1004–9894（2020）03–0019–06

2020–01–09

湖南省哲学社会科学一般项目——学前数学学习困难儿童的执行功能干预研究（15YBA266）

康丹（1981—），女，湖南醴陵人，副教授，博士，硕士生导师，主要从事早期儿童数学认知发展研究．

康丹，张利，蔡术，等．儿童近似数量系统精确性与数学能力的关系研究[J]．数学教育学报，2020，29（3）：19-24．

[责任编校：陈隽、张楠]