课题式教学法探析

曹广福，刘 丹

课题式教学法探析

曹广福，刘 丹

（华南农业大学 数学与信息学院，广东 广州 510640）

课时、学生知识积累、认知能力等多种因素的制约决定了课堂很难做到由学生自主地建立概念与定理，课堂只能以教师教为主．课题式教学要求课堂教学从宏观上把握学科产生与发展的来龙去脉，围绕促使理论产生的一系列问题展开，通过问题的发现、分析与解决从而完成数学的再创造．问题是科学的心脏也是课堂的心脏，教师在课堂上应该引导学生完成3件事：要做什么？为什么要做？以及怎么做？正确理解历史在课堂教学中的作用与意义．

课题式教学；问题驱动；再创造

1 问题提出

中国目前处在教育改革的关键时期，在双一流高校建设过程中，人才培养占有十分重要的地位，从学校的职能看，高校担负着创造知识、服务社会以及为国家培养高层次建设人才的重任．教育改革是一流大学建设必不可少的重要环节之一，正由于此，这些年来，面向课程改革、课堂改革的措施层出不穷，充分体现了国家对教育的重视，从教材改革、教学内容到课堂形式都发生了巨大变化．传统的大学教学无论是内容还是形式都难以跟上科学技术迅猛发展的步伐，改革是大势所趋．从课程体系的设置看，一个典型的特征是每门课程的课时量大大压缩，课程门类增多，课程信息量增大．这就带来一个十分棘手的问题，很多课程的课时数削减了一半甚至更多，教师是减少教学内容、降低教学要求还是改变教学方法？如果按照传统的方式进行教学，很难在给定的学时内完成整个课程的教学任务，如果降低课程要求，采用走马观花的科普式教学则达不到课程的要求，如果对内容有选择地进行教学，就会打乱课程完整的知识体系．教师面临的一个艰巨任务是在不降低课程要求、不减少课程内容的前提下如何用仅有原课程一半的课时讲完全部课程？这是值得每一个教师认真思考的问题．作者在多年实践的基础上提出了课题式教学法，它可以解决课时数与课程内容之间的矛盾，同时也是培养学生创造力的有效途径，体现了大学教育的本质．

2 再论教育的本质

马克思主义教育学认为，教育是一种社会现象，是人类特有的行为．动物也有“教育”，但动物的教育是基于本能的自发行为，动物不具备经验的积累并将之传递给后代动物的能力，动物教育的唯一目的是适应环境以生存，这是动物教育有别于人类教育的根本差别．人类教育的本质不是适应环境，而是培养人具备独立的人格与思考能力，做一个具有自由内心和灵魂的人，这就是孔子所说的“为己”，即塑造自己．卢梭和杜威都提出过“教育即生长”的观点，也就是说，教育的主要目的是让人的天性和能力得到健康长期的发展．

人是唯一有意识的高等智能动物，其教育形式不仅具有多样性（包括语言、文字、动作），还具有明确意识驱动下特定行为的特征．换言之，教育是有意识地以人的身心发展为目标的活动，他是为特定社会服务的，必然会打上特定社会意识形态的烙印，这是教育活动区别于其它社会活动的重要标志，这个标志自然地把教育归属于上层建筑范畴．

关于教育的范畴问题有多种观点，一种观点即上面所说的“教育属于上层建筑”，也有观点认为“教育属于生产力”“教育一部分属于生产力，一部分属于上层建筑”，等等，持不同观点的人也许关注了教育不同的特性．1978年3月18日，在全国科学大会上，邓小平同志在开幕词中指出，4个现代化的关键是科学技术现代化，要大力发展中国的科技教育事业．他着重阐述了“科学技术是生产力”这一马克思主义的观点．1985年3月7日，在全国科技工作会议上，他又再次重申了“科学技术是生产力”的论述．“科学技术是第一生产力”是邓小平基于唯物主义认识论，根据当代科技发展的历史总结出的科学结论．科学技术来自哪里？当然来自教育，来自通过教育激发人的创造力．从这个意义上说，“教育是生产力”的观点无疑是正确的．

教育的本质是什么？这是一个大的哲学问题，或许很难有统一的观点，但教育历来具有两个层面的多重特征，一个层面是人格的培养，即培养具有健全身心与独立人格的思想自由之人，另一个层面则是能力的培养，即培养在某个方面具有创造能力，能服务于社会、创造社会财富的有用之人．这就涉及到一个根本问题，课堂应该教什么？教什么是本质，怎么教是技术，因此教什么比怎么教要重要得多．爱因斯坦讲过：“当你忘记了课堂上学过的一切，剩下的才是教育．”应该如何理解这句话呢？这句话有其正确的一面，也带有一定的片面性，其意思是当你把课堂上习得的知识忘记了，留下的则是能力．比较全面的说法应该是，当把知识背后的思想与方法内化成自身的能力，这才完成了教育的过程．遗忘知识不是教育的特征，恰恰相反，有些知识是不可以遗忘的．例如，数学中的一些基本运算法则到任何时候都不该遗忘，有些知识因为经常使用也不会遗忘，只有那些不常使用或使用时无需具体细节的知识可以遗忘，必要时可以再行查找．教育是涉及教与学两个方面的系统工程，需要教与学两者的配合与协调才能完成．学校教育离不开几个基本要素：教材、课堂、教师、学生，这些要素之间的关系是什么？这是需要搞清楚的问题．在实际的教学过程中，一种普遍存在的现象是教师课堂上只负责传授教材中的知识，学生课内外学习、巩固教材中的知识，这样的现象不仅存在于各学科、各课程中，而且存在了相当长的时间，似乎成了一种普适的教学模式．

3 问题是科学的心脏也是课堂的心脏

何谓课题式教学？根据维基百科的解释：“课题式教学是将学习、设计、研究贯穿于课程教学始终的一种教学方法．也是不同于注入式教学的一种新的教学形式．它打破了旧模式下的‘满堂灌’和‘一言堂’．学生在教师指导下开展学习、研究、讨论和设计，把教、学和做3者有机地结合在一起．她重方法传授、重能力培养、重学生主体作用和学习主动性的发挥．通过这种教学形式，可以使学生的学习能力，设计能力、科研能力、创新能力、与人合作的能力、收集和整理资料的能力、文字和口头表达能力同时得到培养和提高．无疑，这种教学方法不仅是一种具体的教学方法，而且是一种蕴涵现代教学理念的教学思想．”字面上看，这段关于课题式教学的阐释似乎没有问题，那就回到课题本身，先看看什么叫课题．

所谓课题，指的是：“要研究、解决的问题，所以课题背景就是指该问题是在什么情况或条件下产生的，课题研究有什么意义，等等．”从这段话可以看出，课题的心脏是问题，要开展一个课题的研究首先需要搞清楚研究什么问题，为什么要研究这个问题．没有明确问题的课题如同没有心脏的人，失去了泵血的动力，这个课题也就死了．课题涉及的问题是什么样的问题？它包含这样几个方面：

（1）研究什么问题？

（2）为什么要研究这些问题，它的重要性体现在哪里？

（3）解决这些问题的关键是什么？

（4）寻求何种方法解决这些问题？

（5）这些问题的解决能给我们带来什么？

课题研究的目的正是为了解决上述问题，解决了上述问题便完成了该课题的研究．

再次回到课题式教学内涵的界定，在课题式教学的界定中，将重点放在了课堂的形式而非课堂的内容，忽视了科学研究与课堂教学中最重要的东西——问题．这就使得这个定义变得有些空洞，缺少实际的可操作性．

真正的课题式教学应该是什么？简而言之，把某个课程当成课题来研究，也就是弗赖登塔尔所说的把教学过程当成“再创造”过程，这个过程突出的是以问题为内核的探究过程而非形式上的热热闹闹．从教学形式上看，由于课时的限制以及学生知识积累与认知能力的局限，很难在有限的课时内以学生为主完成这种“再创造”过程，数学大师陈省身先生说：“课堂还是应该以教为主”讲的就是这个道理．学生的参与是必要的，应该正确理解学生的参与，课堂并非大家七嘴八舌就是互动了，真正的互动是学生能跟着教师一起在思维的世界里自由地翱翔！也就是说，教师在课堂上应该引导学生完成3件事：

（1）要做什么？

（2）为什么要做？

（3）怎么做？

这是所有学科教学需要解决的3个基本问题，如果不能很好地解决这3个问题，那就谈不上课题式教学，也很难说你的教学是成功的．

与课题不同的是，除了个别的前沿课程，大多数课程都是成熟的理论，学生手中也有教科书，有些学生可能会课前预习，有些学生也可能不预习，面对不同程度及不同学习习惯的学生，课堂该如何进行？这需要一个切实可行的实施方案．顺利开展课题式教学的前提是教师自身具有相关学科的相当素养与眼界，具备一定的研究经验积累，否则，所谓课题式教学注定是空谈．

（1）速度问题；

（2）光学与曲线的切线问题；

（3）面积分析；

（4）最大最小值问题．

微积分在发展的过程中由于自身理论发展与完善的需要，派生出很多问题，例如很多重要原理的产生便是源于微积分自身理论的需要．既然教育是一个再创造过程，教师首先要做的一件事便是追寻历史的足迹，搞清楚某个学科是如何产生的，源于什么样的问题，否则，所谓“再创造”便无从谈起．

然而，诚如在《问题驱动的中学数学课堂教学》（理论与实践卷）（参见文[2]）中所指出的，一个概念或理论的产生往往经历了非常复杂的过程，例如复数从最初的出现到形成一套对数学及自然科学产生重大影响的完整理论经历了两百年的历史，其间经历了众多的人物与历史事件，完全重现历史是不现实的．另一方面，囿于学生的知识积累与认知能力的局限性，有必要将学科的学术形态转换成教育形态以适应学生的认知能力．这就涉及到一个基本问题：如何设计合适的情境？历史上促使一个概念或原理产生的情境不一定适合学生，正如弗赖登塔尔所说：“数学教育要结合学生的生活经验与数学现实．”事实上，任何学科的教学都不宜超出学生的认知能力．所以有必要对促使概念、原理产生的情境作相应的替换，替换的关键是创设适应学生已有经验积累的合适情境，形成有效的问题情境，引导学生围绕着所创设的问题情境展开分析，进而找到解决问题的合适方法．在分析问题的过程中，有可能需要根据问题的难点设计一系列问题形成合适的问题链以分解难点引导学生逐步思考．可见驱动课堂教学的问题与引导学生思考的问题链是属于两个不同层面的问题，两者都是重要的，前者属于教什么的问题，后者则属于怎么教的问题．课题式教学的本质是结合教材以合适的方式再现学科发展的过程，通过问题的发现以及对问题的深入分析与解决建立一个概念或定理，通过这个过程培养学生善于观察各种现象并透过这些现象发现有规律性东西的能力，进而培养发现问题的洞察力、分析问题的思辨力、解决问题的推演力．

有一种观点认为，应该将历史融入课堂，这似乎已经成为广为大家接受的观点，有人喜欢课堂上穿插一些史实以活跃课堂，提高学生的学习兴趣，有人喜欢将历史上的真实情境融入课堂，也有人提倡按照历史的线索进行教学．

“我们研究了著名的威尔逊女子教会学堂的历史。女学生中有一小部分是没有父母的。”翻译把少佐的意思译得有礼有节，一副摊开来大家讲道理的样子。

多了解历史是必要的，但读历史的目的是什么？历史与课堂之间的关系是什么？不清楚这些问题的答案就无法真正将历史融入课堂．一个人完全可以做到在教学过程中看不到任何历史的踪迹，但却在本质上重现了历史，课堂在按照历史发展的逻辑展开！这就涉及前面提到的一个根本问题：“我们为什么要读历史？”读历史的目的并非为了课堂上用历史，而是通过历史搞清楚历史上一个概念为什么产生，一个定理为了解决什么问题，换句话说，要从历史中寻找或通过合情推理梳理出理论产生的根源！搞清楚数学是如何被创造出来的？问题是驱动一切科学产生与发展的源动力，一门学科如果不再有问题，这门学科也就该退出科学研究的历史舞台了！他或许继续被后人崇拜、学习甚至使用，但它已经失去了发展的动力．所以希尔伯特说过：“一门学科如果能不断提出问题，那她就充满活力．”从这个意义上说问题是一切科学的心脏，它也应该成为课堂教学的心脏．课题式教学正是以问题为核心，以解决问题为目的，在分析问题的思辨过程中闪现出数学思想的光芒，在解决问题的推演过程中体现出严密的数学思维．

由此可见，熟悉历史的根本目的不是为了把历史搬进课堂，也不是为了按照历史的线索来讲课，而是通过历史找到促使概念、定理产生的问题，这是课堂教学的第一步，完成了这一步，还需要结合学生的生活经验与已有的数学积累创设合适的情境，然后将找到的问题嵌入到该情境中形成问题情境．情境是为了让学生了解问题的价值，所以情境的真伪就显得很重要了．完成了这一步才正式进入教法层面，即课堂如何围绕着问题情境展开，透过情境对问题进行深入分析从而找到解决问题的方法，这才完成了概念或定理的初步教学，在这个过程中要完成“感知”“类比”“想象”“概括”“抽象”等环节，随之进入“固化”与“运用”环节．在整个教学过程中，由于情境是教师结合学情重新构造出来的，学生从问题情境中未必能看到历史的痕迹，但我们不能说这样的课堂与历史无关，它恰恰反映了概念与定理产生与发展的必然．

不应该机械地理解历史在课堂教学中的角色，例如在《问题驱动的中学数学课堂教学》（复数与三角卷）一书（参见文[4]）中对三角函数的引入使用的便是现代化的汽车仪表板的工作原理．只要遵循学科发展的规律，是否从真实历史的角度开展教学并不重要，历史的价值就在于它反映了学科发展的规律！

4 课题式教学法架构

任何学科都不是空中楼阁，必有其产生的背景，也有其产生的现实或科学意义，这些背景是什么？现实或科学的价值是什么？这是教师在讲授一门课程之前首先要回答的问题，这就好比课题的立项，你缘何选择这样的课题？它的意义与价值何在？如果这个问题不阐述清楚，别人对你的课题必然一头雾水不甚明了，不清楚你到底要干什么．课堂教学也是这样，所以教师在课程的开篇需要从宏观上对课程产生的背景以及意义做出明确的说明，让学生明白学习这门课程的价值何在（参见文[3]）．

在清楚了课程的意义以及需要解决的主要问题之后，将进入后续各章的学习，每一章既有相对的独立性，各章之间又有着重要的逻辑关联，特别是数学课程通常逻辑环环相扣、内容层层递进，所以在宏观上理清楚课程的来龙去脉之后，各章具体的教学环节如同一个个的子课题，在完成一章的教学之后，要找到不同章节之间的逻辑关系进而进入下一个章节（下一个子课题）的学习直到整个课程的完成．每一章都要面对同样的问题：（1）课题的意义；（2）在课程中的地位（或作用）；（3）需要解决的问题；（4）解决问题的途径．不同章节之间的逻辑关系要梳理清楚，即每一章节解决了上述4类问题后还需要进一步分析下一步需要进行的工作从而顺利进入下一个章节．整个课程的教学过程如同一个大的项目被分解成若干子课题层层推进，当完成整个研究过程后，课程的教学任务也就完成了．

课题式教学的内核是问题，教师对相关历史的了解程度，对这门课程产生的背景以及该课程在发展的过程中都面临着什么样的问题是决定课题式教学成功与否的关键．无疑，课题式教学给教师提出了更高的标准与要求，他不仅要求教师对所教的课程具有相当程度的理解，还必须清楚课程中许多重要概念、理论的来龙去脉与前世今生．课题式教学的基本架构如图1所示．

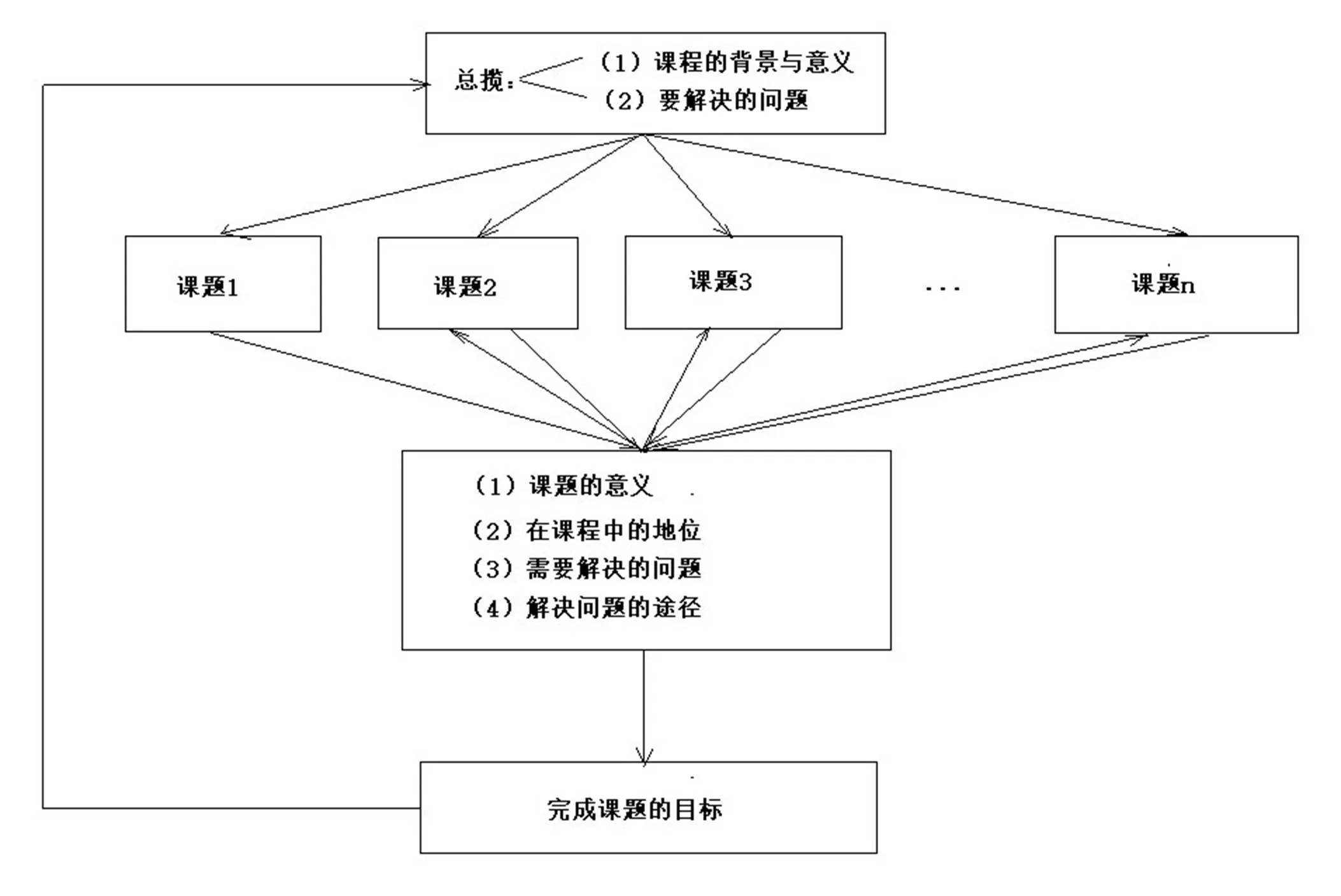
图1 课题式教学法基本架构

从这个架构图可以看出，一个完整的课题式教学是从总揽到课题1，通过课题1中的4类基本问题的研究完成第一章的教学，然后通过逻辑关系的梳理清楚下一步该做的工作，从而进入课题2（第二章）的研究，以此类推，直到完成课题（最后一章）的研究．当整个课题的目标达到后，再回到开始时抛出的问题，首位呼应，课程的教学就全部完成了，课程的教学过程就是课题的研究过程，这才是真正的课题式教学．

课题式教学过程好比踏着研究者的足迹将这门理论产生与发展的历程完整走了一遍，冰冷的符号再次变成了火热的思考．但它不是简单的理论重建，而是经过教师的精心策划、重构所进行的有限的再创造，在这个过程中离不开教师的主导作用．那种将课题式教学理解成“学生在教师指导下开展学习、研究、讨论和设计，把教、学和做3者有机地结合在一起”是对课题式教学的机械化理解．无论是中学还是大学，课堂都很难做到“以大家都动手”为主，必然是教师教为主．那种流于形式的“教、学和做3者有机地结合在一起”不仅难以带来学生能力的提升，还会大大影响教学效率．尤其是中学生正处于打基础的黄金时期，培养学生发现问题与分析问题的能力、提升思维能力才是中学教师的根本任务，而要做到这一点，必然需要以教师示范为主．大学课程则由于课时数有限，课堂容量比较大，很难有时间供学生独立地发现问题、分析问题并解决问题，也只能以教师教为主．可以在每个子课题（章节）的开始引导学生去发现问题，但分析问题的过程则需要以教师为主，让学生紧紧跟着教师的思路走，慢慢学会独立思考．在每个子课题的最后则可以组织学生进行反思，这个环节可以在教师引导下由学生来完成．

课题式教学不仅一改以传授知识为主的经典教学方式，而且极大增加了课堂教学的弹性，无论是少课时还是多课时的课程都可以按照这样的模式开展教学，对于少学时课程可以采取粗线条的方式，但需要学生课后花更多的时间，对于多学时课程，则可以围绕着问题深入剖析，细节化展示概念、定理的建立过程，这才是真正意义上数学的再创造．

[1] 弗赖登塔尔．作为教育任务的数学[M]．上海：上海教育出版社，1999：107–110．

[2] 曹广福，张蜀青．问题驱动的中学数学课堂教学（理论与实践卷）[M]．北京：清华大学出版社，2018：11–13．

[3] 曹广福．将教学过程当成科研过程[J]．中国大学教学，2015（12）：11–14．

[4] 曹广福，卢建川，沈威．问题驱动的中学数学课堂教学（复数域三角卷）[M]．北京：清华大学出版社，2019：45–72．

On Project-Based Mathematics Instruction

CAO Guang-fu, LIU Dan

(School of Mathematics and Information, South China Agricultural University, Guangdong Guangzhou 510640, China)

The constraints of class hours, students’ knowledge accumulation, cognitive ability, and other factors create challenges for students to independently construct concepts and theorems. Thus, classroom instruction must be led by teachers. Project-based instruction requires that classroom teaching take into account the historical origin and development of the subject from a global perspective and then build up a theory through exploring a series of problems. The process of rediscovering mathematics is completed through discovering, analyzing, and solving that series of problems. Problems are at the heart of science, as well as at the heart of classroom instruction. Teachers need to facilitate classroom instruction to address three questions: What do you want to do? Why would you like to do that? And how are you going to do that? It is important to appropriately understand and use history in classroom instruction.

project-based instruction; problem driven; rediscovery

G424.1

A

1004–9894（2020）03–0032–05

2020–04–07

国家应用数学中学粤港澳大亚湾应用数学中心资助项目——问题驱动的中小学数学教育研究（2020B1515310020）；华南农业大学教育教学研究和改革项目——新工科背景下高等数学混合式金课的研究与实践（JG19074）

曹广福（1960—），男，江苏海安人，教授，博士，博士生导师，首届国家教学名师奖获得者，入选第二批国家“万人计划”教学名师，主要从事数学研究与数学教育研究．

曹广福，刘丹．课题式教学法探析[J]．数学教育学报，2020，29（3）：32-36．

[责任编校：周学智、陈汉君]