综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷
2020-07-03张玉环
张玉环,周 侠
综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷
张玉环,周 侠
(河南大学 数学与统计学院,河南 开封 475004)
自2014年高考改革启动以来,公众对改革实施成果及高考考题质量愈发关注,因此,有必要从国际视野审视中国的高考.采用定性和定量相结合的方法,研究2015—2019年中国理科数学全国Ⅰ卷与法国本土的业士考试(也称毕业会考)试卷,进行难度分析和典型案例分析,结合中国新高考改革要求及学科核心素养,提出新高考命题建议:重视“过渡”,体现基础性;加强“整合”,体现综合性;注重“背景”,体现应用性;关注“开放”,体现创新性.
法国数学;高考试题;综合难度;比较研究
1 问题提出
2014年9月印发的《国务院关于深化考试招生制度改革的实施意见》标志着新一轮考试招生制度改革的全面启动[1],随着近年来高考改革的逐步深化,大众对高考试卷的关注度也逐步提升.2019年6月发布的《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》强调试题难度的设置要科学合理,符合课标与学生实际情况[2].2019年发布的《普通高等学校招生全国统一考试大纲》总纲也明确提出高考应具有适当的难度[3].
高考数学试题的难度一直以来都是老师、家长以及考生迫切关注的问题.对难度的研究可以更好地评估试卷的质量,帮助老师更透彻地解析试卷,也给学生和家长一些启示与导向.而且,从国际视野看高考考题难度可以全面、准确地认清难度定位,以便合理把控国内高考考题难度,同时为考题命题方式提供一些参考.
蔡元培先生认为:在世界各国之中,法国文化与中国最相契合[4].被誉为“伟大数学家摇篮”的法国,在现代也为数学界培养了众多菲尔兹奖得主,这在一定程度上反映出其教育与选拔制度的优越性.法国历史上有过多次教育改革,现已形成了一套完备的教育评价与选拔体系,而业士考试这一传统经过不断完善仍被保留了下来.业士考试(下面简称法国高考)在法国教育中的地位与作用类似于中国的高考,测试内容与测试对象与中国高考契合度也很高[5].国内关于法国高考的研究集中于法国高考制度与作文、哲学等学科,对法国高考数学考题的研究较少,如戴桂生对2006年数学理科试卷进行译注[6],龚妙昆对法国会考制度简介以及2007年试卷进行翻译[7],胡凤娟结合2014—2018年考题对法国主题式命题的特点加以介绍[8].对于法国数学试卷的难度研究寥寥无几.因此,可以通过中法高考的考题设置进行难度研究,并结合法国典型案例分析,为中国的高考改革提供一些参考建议.
2 研究设计
2.1 难度模型
总体难度的概念在2001年由Nohara提出,现今关于数学难度的研究已有一些成熟的结论与模型,其中国内较为认可的是鲍建生提出的数学习题评价的综合难度系数模型,常用于评价数学习题、教材与课程难度.王冰等人基于该模型,结合地理学科特点和学生认知发展特点构建了有关地理教材习题的综合难度模型,具有较强的学科专业性[9].武小鹏等人结合高考试题特点,对综合难度模型做出了改进,加入思维方向、有无参数两个因素,形成了更适合高考数学考题,同时也更契合数学学科核心素养的难度系数模型,这里将选取该模型来分析近5年来中法考题的难度[10].
由于课标要求不同,中国高考与法国高考在试题类型上有很大不同.法国高考没有选择与填空,考题由主观题的形式给出,共有4道大题,按照主题划分,总分20分,考试时间4小时.选做方面中有一道专业选做题与一道非专业选做题,难度往往不同(专业选修的数学课程权重系数为9,非专业选修的数学课程权重系数为7),由学生根据自身情况选做.而中国高考全国I卷试题有选择题、填空题、解答题3种题型,有2道或3道选做题,总分150分,考试时间两小时.鉴于二者题型与总题数的差距,难度系数的计算不仅要用到各因素、各水平的题目数,还要用到试卷的题目总数进行加权平均,以消除题目总数不一致带来的影响.
改进后的难度系数模型包含背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、认知水平这7个因素,不同因素各水平编码与权重具体见表1.
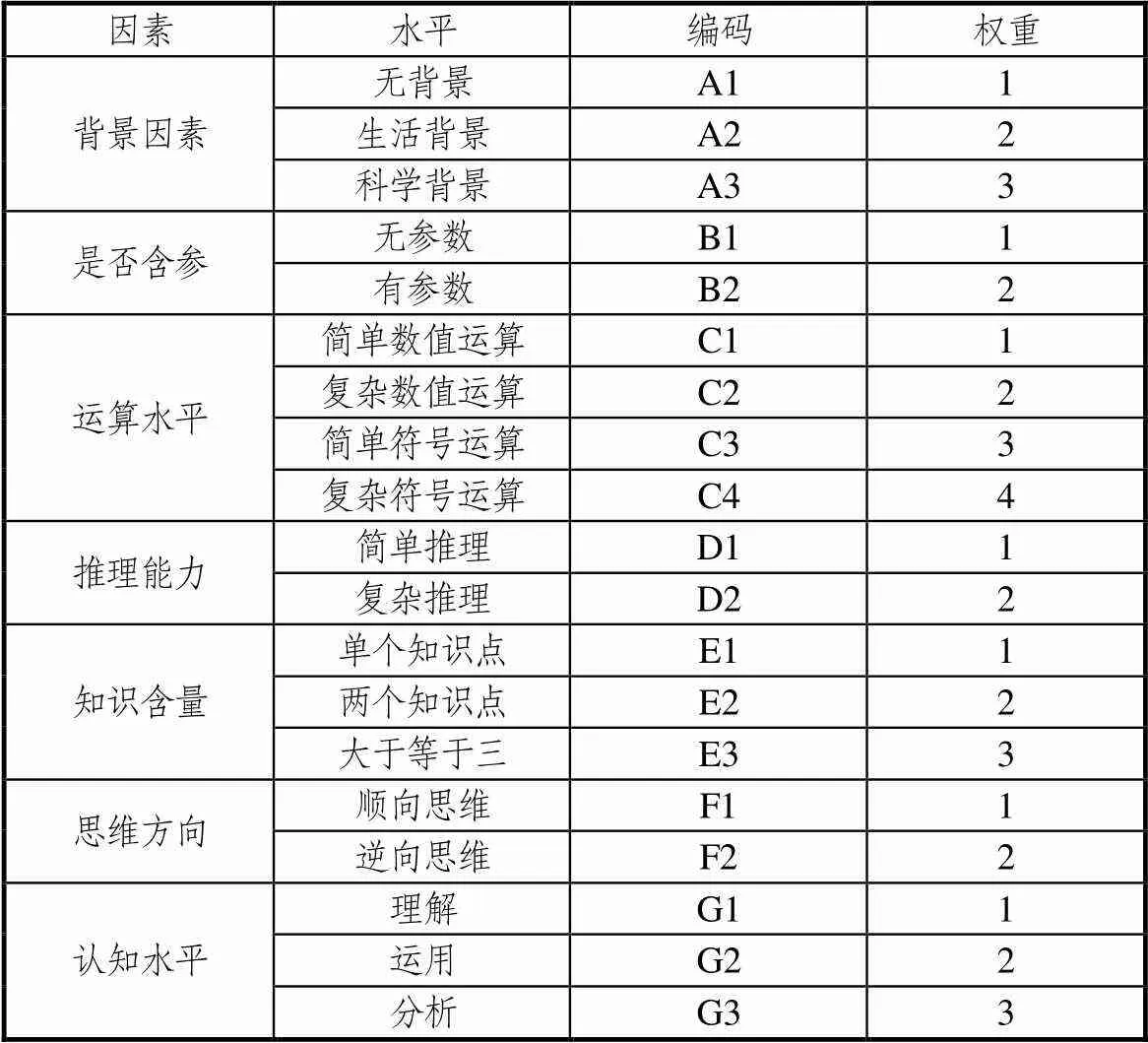
表1 综合难度系数模型的结构
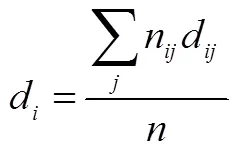
2.2 研究对象
为使研究结果更有代表性,研究对象选取适用考生最多、范围最广的试题.因此,选取2015—2019年的理科数学全国I卷与法国本土试卷,分别用CH和FR表示[11].由于法国有两道难度不同的选做题,故将“必做题+不同的选做题”看作不同套试卷,即“必做题+非专业选做题”(简称非专业选做试卷)、“必做题+专业选做题”(简称专业选做试卷)分别表示为FRI和FRII.
2.3 编码方法
按照难度系数模型的7个因素不同水平对考题进行编码,编码示例如下.
例1(2019全国I卷)
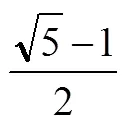
此题编码为A2(生活背景),B2(有参数),C1(简单数值运算),D1(简单推理),E1(单个知识点),F1(顺向思维),G3(分析).
例2(法国2016年高考中文译题)
某工厂采用两条生产线生产一电子元件.生产线A生产40%的元件,而生产线B生产剩余的部分.由于所生产的部分元件存在瑕疵,使得该工厂无法以预期的速度完成生产.其中,生产线A生产的产品中,20%的元件具有该瑕疵,而在生产线B的产品中只有5%存在该瑕疵.从这个工厂生产的元件中随机选择一个,假设:事件A:“该元件来自生产线A”;事件B:“该元件来自生产线B”;事件S:“该元件没有瑕疵”.证明:事件S发生的概率为(S)=0.89.
此题编码为A2(生活背景),B1(无参数),C3(简单符号运算),D1(简单推理),E2(两个知识点),F1(顺向思维),G1(理解).
3 研究过程与结果
下面主要分维度展示各因素的不同水平占比情况,首先依据2015—2019这5年数据的平均值,横向对比中法差异;再对二者差异显著的因素采取逐年对比分析的方法纵向观察其变化情况;最后整体对比分析中法试题的综合难度.
3.1 背景因素
法国高考的4道主观题围绕4个主题考查不同模块知识,以近5年试卷来看,至少两道主观题是围绕生活背景中的一个大情境展开的,且每年都有科学背景题目.以2019年试题为例,第一道题围绕“隧道型温室”的形状展开,考查函数相关知识;第二道题围绕某游戏平台的两类游戏展开,考查概率与统计相关知识;第三题中的第五小题是借助算法的结果来考查不等式内容的.即2019年试卷中的4道主观题中,有3道涉及到背景因素,有背景试题比例远高于中国,以下通过具体数据来说明这一情况.
背景因素分为无背景、生活背景、科学背景3个水平,中法高考试卷各水平的题目数占比如图1.
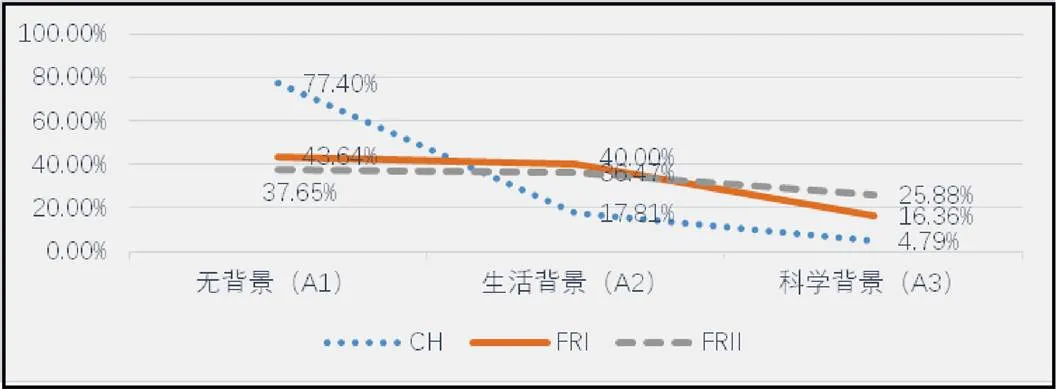
图1 背景因素不同水平中法折线对比
结合图1可以看出,背景因素方面,法国两套题呈现结果相似:无背景题目数与生活背景题目数近乎持平;科学背景题目所占比例远小于前两者,FRII卷较FRI卷比例稍高.对比法国,中国无背景试题较多,占比近八成;在生活背景题目所占比例上也表现出较大差距,法国生活背景题目占比超过中国的两倍;中国科学背景题目占比低于5%.
图2为背景因素各水平占比逐年变化图.从图2中可以看出,中国试题在背景因素方面,不同年份各水平占比情况较为稳定.其中,无背景因素占比均高于75%,低于80%.科学背景题目占比2015年与2018年、2019年较为一致,2016年与2017年相等,总体差别不大.法国则在不同年份上表现出一定差异,科学背景题目比例2015—2018年逐步提升,但在2019年骤减,另外两个水平也无明显规律.法国在科学背景方面,会穿插一些含有新的科学概念等的试题,如2016年出现的“有理线”,2017年出现的“几乎等腰直角三角形”(边长为、+1、的直角三角形,简称TRPI),2018年出现的“大对角线”“垂心四面体”等概念.
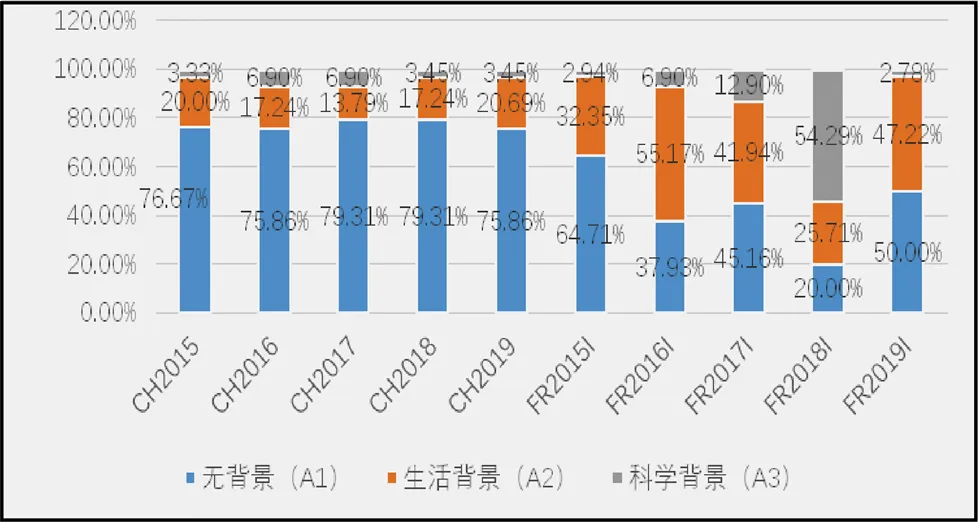
图2 背景因素不同水平占比逐年变化
为更细致地了解中法高考题目的背景因素,按照PISA2012情境的5个划分维度:健康、自然资源、环境、灾难、科技前沿[12],对中法近5年来试题的小题数进行统计,具体见表2.2019年中国试卷小题总数31,法国非专业选做试卷和专业选做试卷的小题目总数分别为36、37,各年总题数波动较小.两国试卷小题总数差别不大,具备对照分析的条件.
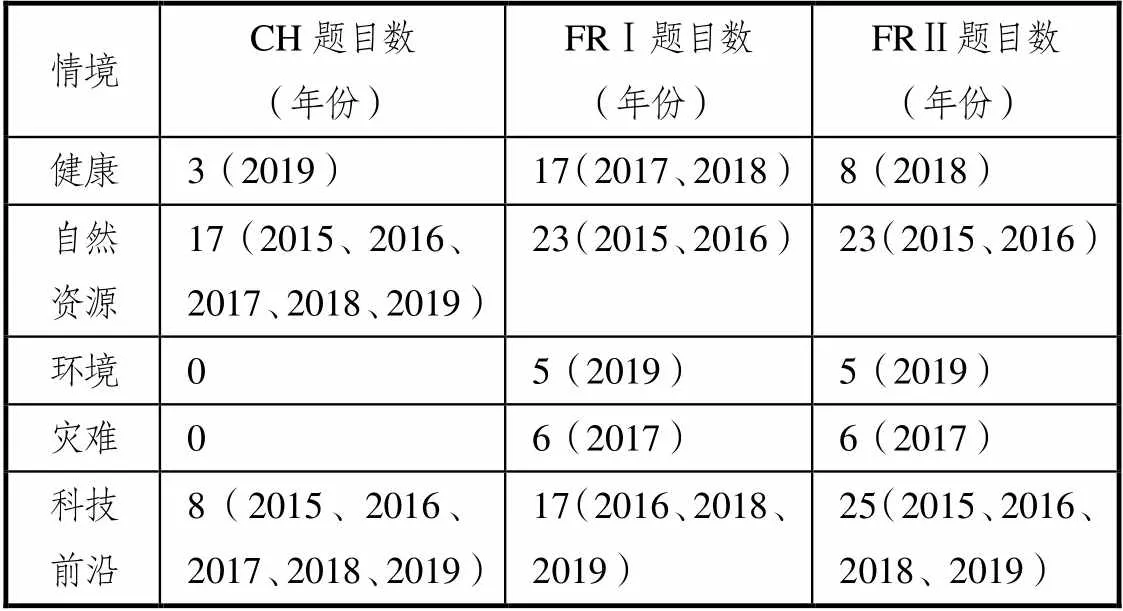
表2 中法具体情境划分
从表2中可以看出中国试题在背景涉及范围和数量上的表现逊于法国.具体背景如下,法国试题涉及健康维度的背景有传染病模型(2017、2018);自然资源维度下,涉及与生活质量因素相关的情境有工厂生产(2016)、商品销售(2015);环境维度下,涉及与环境影响有关的温室种植(2019);灾难维度下,涉及风险评估有关的气象探测(2017);科技前沿维度下,涉及运动与休闲因素有关的体育活动(2016)、游戏推广(2019)以及生活现象的数学解释(2018)等方面;中国试题背景多涉及自然资源维度与科技前沿维度,如工厂生产(2016、2017、2018)、古代文化(2015、2017、2018、2019),穿插以体育(2015)、交通(2016)等背景的题目.
3.2 有无参数
因素有无参数分为两个水平,中法高考的不同试卷各水平的题目数占比如图3.
在有无参数方面,中国卷和法国Ⅱ卷体现出高度的一致性,有参数题目占比近三分之二.法国包含非专业选做题的Ⅰ卷有参数比例较低于包含专业选做题的Ⅱ卷,但总体仍表现为有参数题目多于无参数题目.中法含参数题目多考查函数知识,另外,中国在选做题中专有参数方程题目.
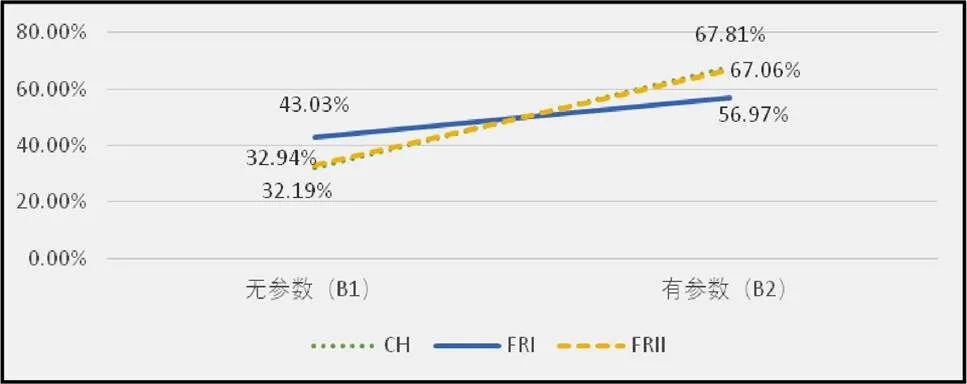
图3 有无参数因素不同水平中法折线对比
3.3 运算水平
因素运算水平分为4个水平,中法高考的不同试卷各水平的题目数占比及逐年对比情况如图4和图5.
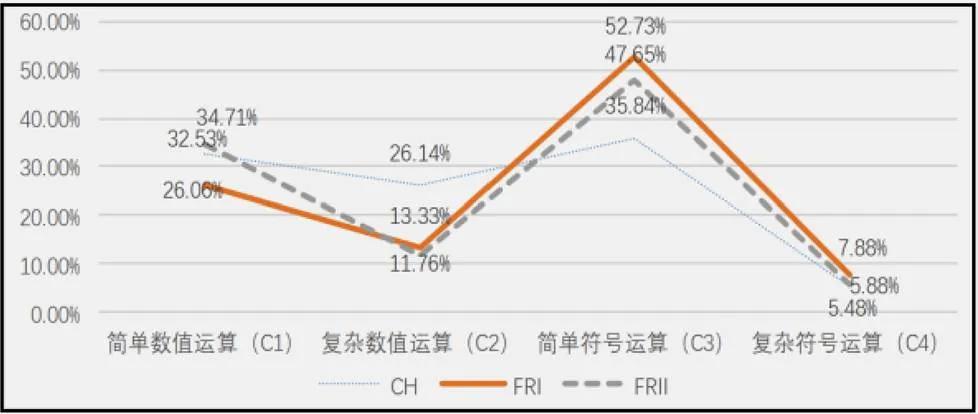
图4 运算水平因素不同水平中法折线对比
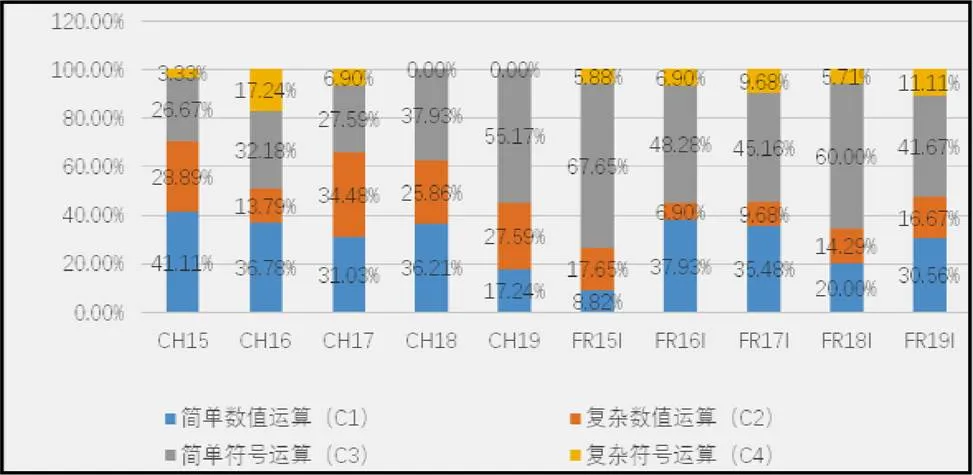
图5 运算因素各水平占比逐年变化
从图4中可以看出,中法试题在运算水平表现出的总体趋势一致:从低到高的比例依次是复杂符号运算、复杂数值运算、简单数值运算、简单符号运算.中法差别主要体现在复杂数值运算和简单符号运算上,前者中国试题比例近法国的二倍,后者法国卷占比较高.从图5中可以发现:中国简单数值运算的题目占比大体上逐年递减;复杂数值运算平均比例高于法国;简单符号运算题目比例有所上涨但多低于法国;复杂符号运算方面双方类似.
3.4 推理能力
因素推理能力分为两个水平,中法高考的不同试卷各水平的题目数占比及各年份占比情况如图6和图7.
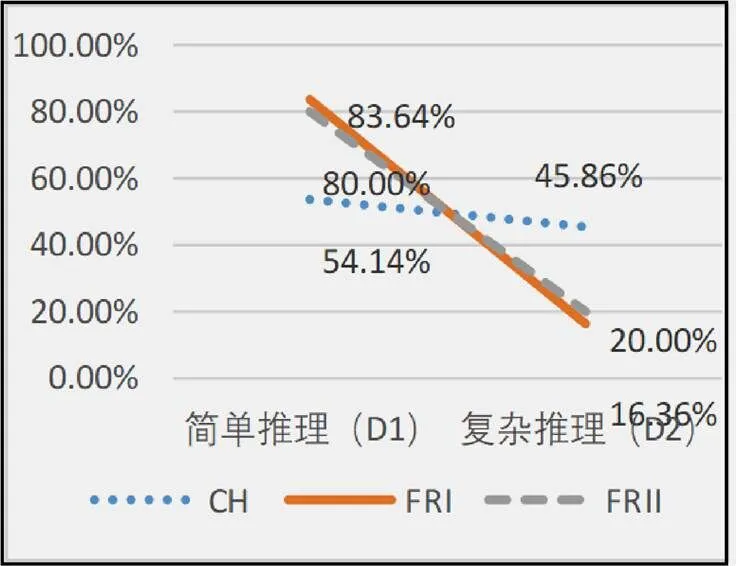
图6 推理能力不同水平中法折线对比
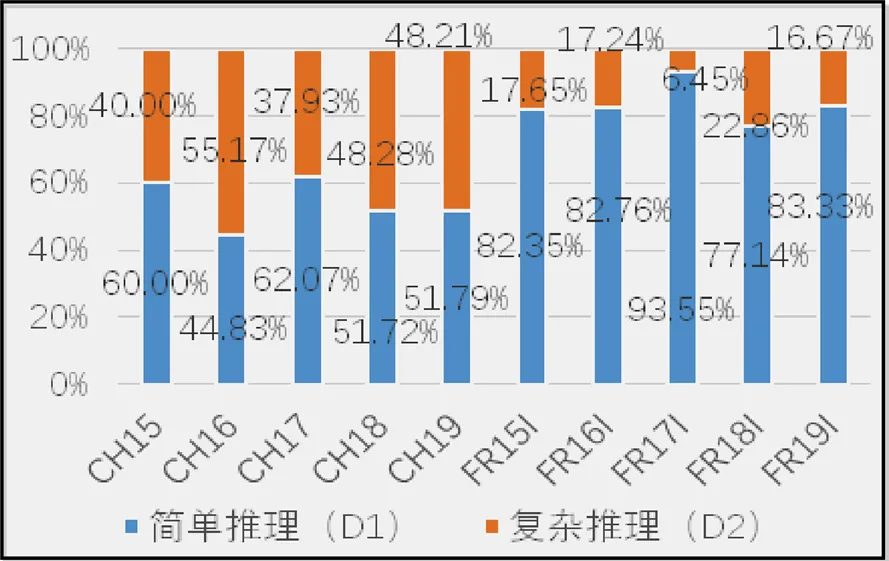
图7 推理能力各水平占比逐年变化
从图6中可以看出,推理能力方面,法国两套试卷结果相似:简单推理题目比例超过八成,远高于复杂推理题目比例.而中国卷简单推理题目比例略高于复杂推理,二者相对均衡.从图7变化趋势来看,中国各水平题目趋于稳定,占比趋于均衡;法国复杂推理题目比例近两年略有提升,但仍远低于中国.中法对比可以看出中国对考生推理能力严要求、高标准.
3.5 知识含量
知识点按照知识模块进行划分.由于两国课标不同,考查知识点有着一定差别.中国考查知识点可参考考试大纲,法国考点见表3.
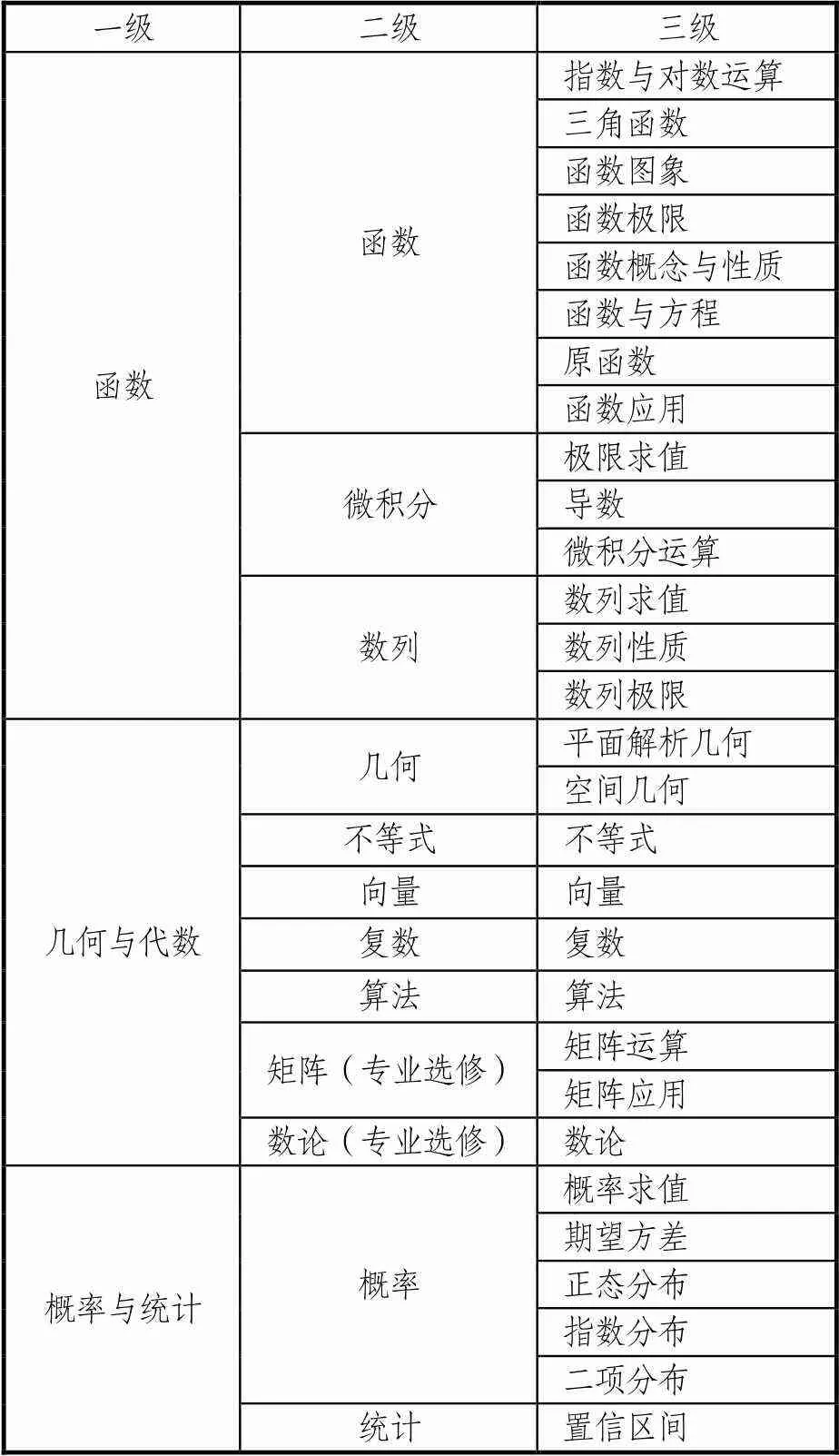
表3 法国考点
两国常考考点及所占分值比例都有很大不同.以2019年法国卷为例,总分为20分,其中函数大题6分,占30%;概率与统计大题5分,占25%;代数大题4分,占20%;选做I卷为几何,II卷为代数,计5分,占25%.中国以2019年全国I卷为例,总分为150分,概率与统计的考查为一道选择,一道填空与一道解答题,共22分,占总分14.67%,低于法国;几何部分为两道选择,一道填空与两道解答题,共39分,占26.00%,高于法国;其余考查代数与函数相关知识,包含选做题,为89分,共占59.33%.
中国常考考点为:集合运算、复数、函数图象与性质、圆锥曲线的几何性质、算法框图、平面向量的基本运算、导数、数列、坐标与参数方程、不等式、三角函数、分布列、线、面关系等.
法国常考考点为:数列极限、函数图象与性质、导数与积分、概率树、正态分布、数学归纳法、复数、解方程、算法、矩阵、线面关系、向量等.
因素知识含量分为3个水平,中法高考的不同试卷各水平的题目数占比如图8.
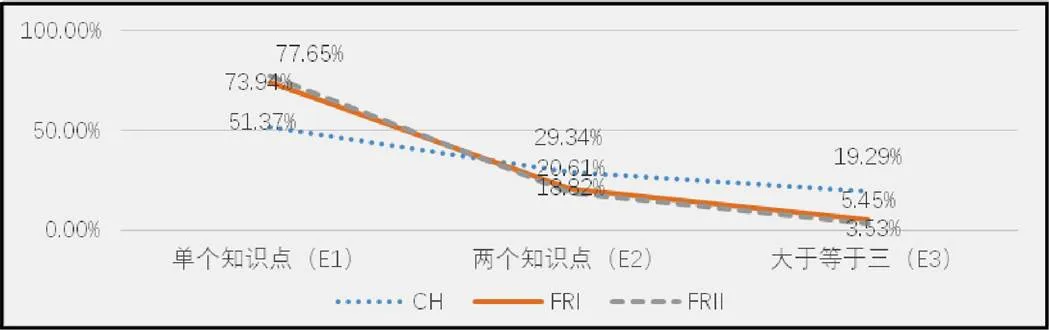
图8 知识含量不同水平中法折线对比
从图8中可以看出,中法试题在知识含量方面的总趋势为:单个知识点题目占比多于两个知识点,多于大于等于3个知识点题目.中国单个知识点的题目比例约一半,不同水平变化坡度小于法国.法国包含单个知识点题的比例超七成.而知识点含量大于等于3的题目,法国两套试卷占比均不超过6%.
从中国多知识点题目的比例中不难看出全国卷在命题时对知识综合的重视.在多知识点题目中,客观题所占比例较多,如集合运算常结合解不等式知识考查,曲线方程与向量知识常结合考查,三视图常与几何体面积、体积公式结合考查,平面的截面问题与直线、平面位置关系以及异面直线所成角几个知识点常综合考查,数列章节各知识点可交叉结合,坐标系的转化与不同几何图形之间位置关系可相结合.
总体来说,法国有较多考查单个知识点的题目,而中国倾向于知识的综合运用,有意识关注知识之间的关联.
3.6 思维方向
因素思维方向分为两个水平,中法高考的不同试卷各水平的题目数占比如图9.
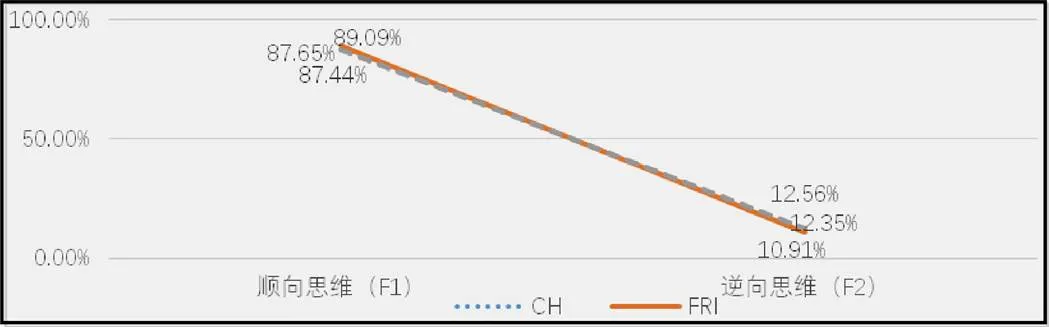
图9 思维方向不同水平中法折线对比
从图9可以看出,在思维方向上,中法试卷体现出高度一致性:以顺向思维题目为主,逆向思维题目为辅,其中顺向思维题目占比超过85%.
3.7 认知水平
因素认知水平分为3个水平,中法高考的不同试卷各水平的题目数占比及各年份变化如图10和图11.
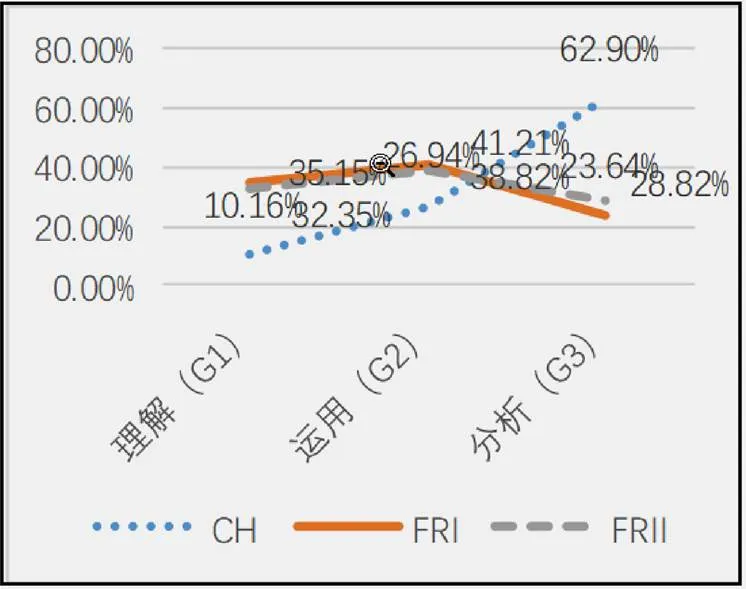
图10 认知水平不同水平中法折线对比
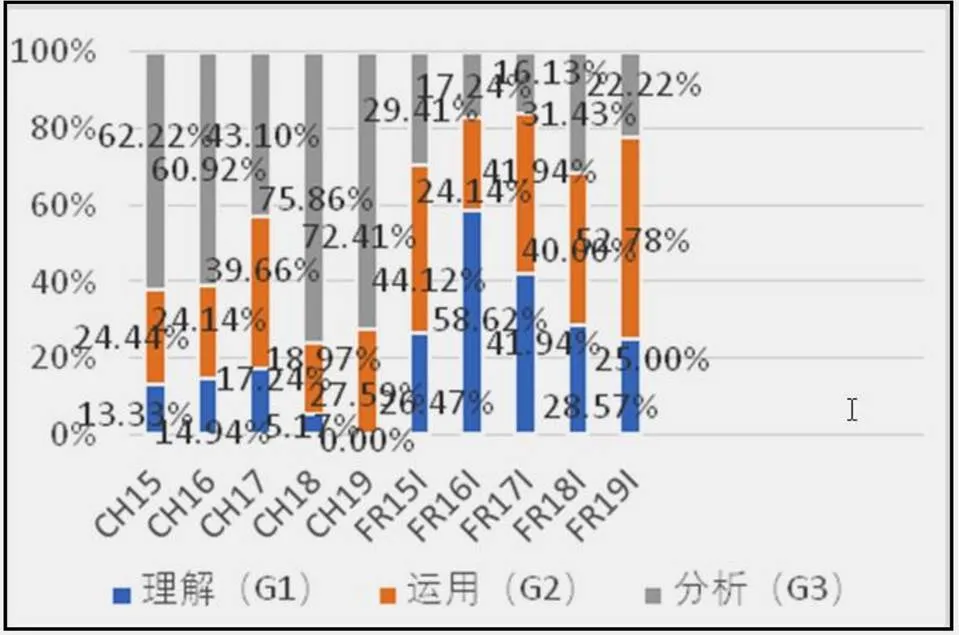
图11 推理能力各水平占比逐年变化
在认知水平方面,中法试题呈现出相反的结果.中国分析水平的试题占比最高,而理解水平试题占比很低,各水平落差较大.法国则是运用水平试题占比较大,分析水平占比较小,各水平试题比例相对均衡.从不同年份来看,中国理解水平试题占比先递增再递减,分析水平试题比例先递减再递增.法国理解水平试题近年呈现出递减的趋势,但总体占比超过中国.运用水平试题除2016年外,比例均相似.分析水平试题整体占比较低,但近两年较前3年在增多.
分析水平试题中题目暗含条件较多,需要深入挖掘、分析并综合运用各知识点,对学生知识掌握方面的要求比较高.中国分析层面的题目占比大,在很大程度上增加了全国卷的整体难度,也体现出中国对考生知识认知与运用水平的高度要求和考题的选拔性功能.
3.8 各因素综合难度
将近5年试题综合,可计算各因素难度及综合难度系数.CH、FRI、FRII综合难度系数分别为14.35、13.32和13.54,各因素难度系数的雷达图如图12.
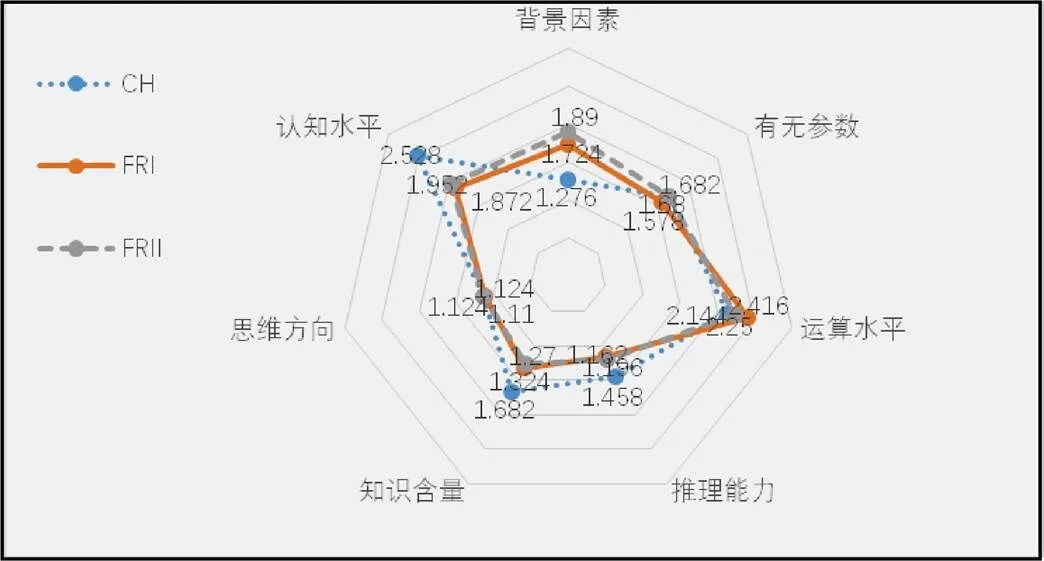
图12 不同因素难度系数雷达图
由图12可以看出,在有无参数、运算水平和思维方向上,中法体现出了一致性,背景因素方面中国难度明显低于法国,而推理能力、知识含量和认知水平上,中国难度更高.试卷的综合难度系数从高到低依次为:CH、FRII、FRI.
3.9 试卷综合难度
结合各因素的权重系数,按照综合难度系数计算方法可算得各套试卷的综合难度系数,见图13.
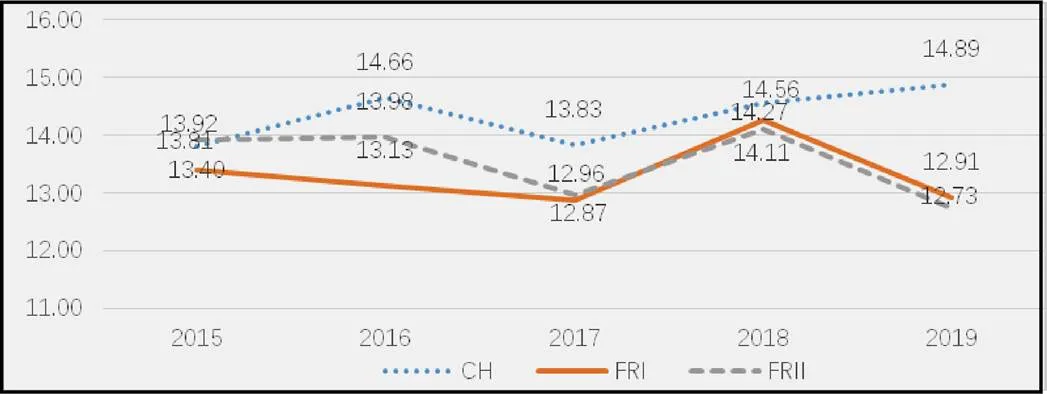
图13 中法各试卷综合难度系数
从图13中可以看出,除2015年综合难度略低于法国II卷外,其它年份中国卷的综合难度大于法国卷,法国卷2015年与2016年专业选做试卷的难度更大,而近3年专业选做试卷和非专业选做试卷难度相似(专业选做试卷的知识点包括矩阵、数论等,这些知识难度比较大,但在难度模型中很难量化计算).逐年对比可以发现,中国卷在开始的波动后近两年难度在上升,法国卷仍处于一个波动状态.中法近年来试题综合难度波动范围不超过1.5,总体均处于稳定状态.
4 典型案例
下面将通过典型案例分析中法两国高考的命题方式.
案例1(法国2019年高考中文译题)
计算机平台提供两类游戏:A类游戏和B类游戏.
Part A
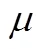
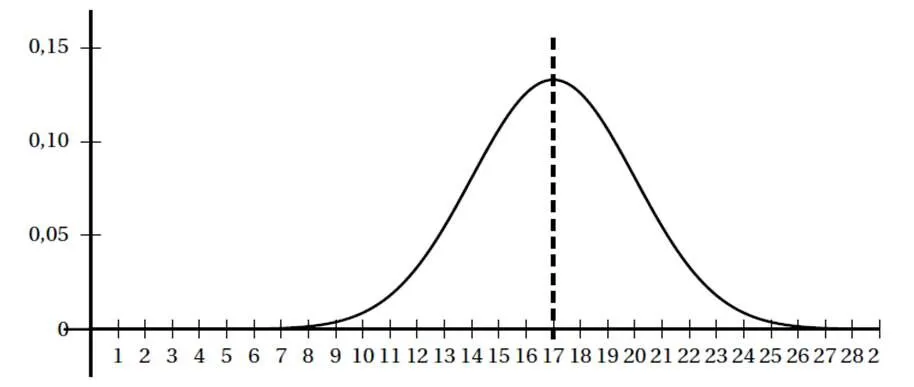
1.
1)计算玩A类游戏时长的均值.
2)根据上图求玩B类游戏时长的均值.
2. 随机选取一类游戏,求游戏时长低于20分钟的概率.(结果精确到百分位)
Part B
一旦玩家结束一场游戏,平台会给他推荐一种新游戏.
——如果该玩家玩的是A类游戏,平台再次给他推荐A类游戏的概率是0.8;
——如果该玩家玩的是B类游戏,平台再次给他推荐B类游戏的概率是0.7.
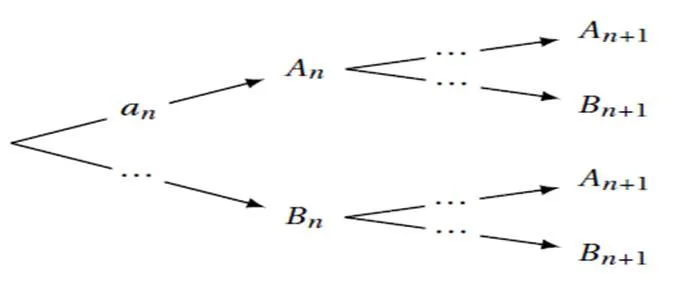
1. 在答题卡上画出并完善概率树.
证明:对于任意非零自然数,成立:
记玩家在第一局选择A型游戏的概率为,其中是区间[0, 1]上的实数.
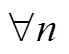
2. 特例研究.本题设=0.5.
1)用数学归纳法证明:对于任意非零自然数,成立:0≤a≤0.6.
2)证明:数列{a}单调递增.
3)证明数列{a}收敛,并求其极限.
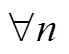
1)证明:数列{u}为等比数列.
3)求数列{a}的极限.该极限是否取决于的值?
4)平台打算在两类游戏的开头各投放一个广告,喜欢玩电子游戏的玩家观看次数最多的广告应该是哪一个?
案例2(法国2015年高考中文译题)
连锁企业希望通过向特权客户提供代金券来留住客户,客户会收到一张绿色或红色的印有其价值的代金券.每个商店分到四分之一的红色代金券和四分之三的绿色代金券.抽到价值为30欧元的绿色代金券概率为0.067,价值在0到15欧元之间的绿色代金券概率未知;抽到价值为30和100欧元的红色代金券概率分别为0.015和0.010,价值在10到20欧元之间的红色代金券概率未知.
该连锁企业的一家商店的200名特权客户中,有6人抽到了价值大于或等于30欧元的代金券.店长认为这个数字不足,并对从连锁店向各个商店代金券的随机分配产生怀疑.他的怀疑合理吗?
背景方面,案例1的背景为游戏平台,案例2的背景为商店抽奖,可以看出,法国高考命题时注重题目的背景与知识的运用,培养学生数学抽象能力与数学应用意识.
分析与推理方面,法国考题的鲜明特点是:注重理解层面基础知识的考查,题目层层铺垫,前面的题为后面的题提供思路,增多了题数,减小了难度.如案例1的Part B,题1的1)可根据题意来完善概率树,考查对题目的理解;2)则可根据1)中的数据和全概率公式来证明,1)中的数据为2)的解答提供基础.题2中1)在题目中给出了方法指引,2)中要证明数列递增,只需计算前后两项之差,判断其正负:
即可推出数列{a}单调递增.而3)的证明则利用题1)和2)的数列递增且有上限的结果.每一步都为下面的题提供思路,连起来就是一个完整的思路与知识体系.
知识点方面,概率树是法国高考的一个高频考点,而中国对此涉及较少;数列求极限问题是中国高中课标选修的内容.正态分布、数列性质等也是法国常考考点.考点综合方面,以Part A的题1为例,先考查均匀分布的均值,再考查正态分布的均值,两道题都是对基础概念的理解.一道题只考查单个知识点在法国考题中是常见的,而中国更注重知识的综合,将两个及以上考点结合抽象出一道考题.
开放性方面,案例2是一道开放性试题,学生可以选择合适的置信度,答案言之有理即可,这可以帮助培养学生的创新思维与应用意识.而中国则缺少这样的开放性试题.
另外,法国考试形式较之中国更加多元化,设置有数学活动与口试.数学考试时间长于中国,为4个小时,对学生的做题速度要求较低.这些都在一定程度上降低了法国高考的难度.
5 讨论与展望
5.1 对中法高考研究的拓展
现有的法国高考研究多集中于其制度改革,穿插试卷翻译,以及对其主题式命题方式的研究,对难度没有涉及.从难度视角和国际视野下看高考,通过横向、纵向对比与典型案例分析,同时结合国家政策及核心素养对高考改革提建议的研究方式,为高考研究提供了新的视角.
5.2 研究的局限与展望
首先,采取的难度模型各因素所占权重人为给出,具有一定的主观性,缺乏强有力的理论与数据支撑.其次,高中数学核心素养中的直观想象能力在模型中未能有很好的体现.另外,考试的时间会在很大程度上影响试卷综合难度,在该模型中未能考查.最后,试题所考查的知识内容本身难度不同,但缺少统一的量化标准,难以量化,在难度模型中也未能考查.在今后的研究中,希望能进一步优化数学难度模型,使其更适用于高考研究.同时,对中法高考从知识点层面进行更深度的考查.
6 思考与建议
2014年9月国务院颁布了《关于深化考试招生制度改革的实施意见》,2016年教育部考试中心在此基础上明确了“一体四层四翼”的高考评价体系,其中,“四翼”为新时代高考内容改革的考查要求,即“基础性、综合性、应用性、创新性”,回答素质教育下“怎么考”的问题.而2019年《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》中提出深化考试命题改革的方向,比如创新试题形式;加强情境设计;注重联系社会生活实际;增加综合性、开放性、应用性、探究性试题,都与“四翼”牢牢贴合,因此,高考命题建议把握好以下4个方面.
6.1 重视“过渡” 体现基础性
关于推理与分析因素,中国试卷的复杂推理题目比例远高于法国,理解水平试题占比较之法国非常少,综合难度方面,全国卷的综合难度高于法国卷,且难度在提升.同时,受考试时间与考查形式的影响,中国试题体现出来的特点是难度高,不够基础.这使得中国考生对数学考题有畏惧心理,甚至“望数学生怯”.而法国简单推理试题较多,从基础知识点开始,层层铺垫引导,帮助学生解题.
推理能力在数学核心素养中体现为逻辑推理,高中涉及推理大体有合情推理与演绎推理两种.一套完整的试题,二者都必不可少,前者有铺垫引导作用,培养逻辑思维.后者旨在开发学生思维,避免定式.黄志华与渠东剑通过调查南京市学生得出,高中学生的逻辑推理处于中等水平[13].故在提问形式中给学生一些过渡,提供思路的推理题更易被接受.另外,理解水平试题是对基础知识的直接考查,学生分析题目能力的提升离不开对基础知识的理解[14],课程目标由“双基”转向“四基”,基础知识一直占据重要地位,其对现代数学教育的重要程度可见一斑.因此,高考在发挥其选拔性作用的同时,也要考虑到考题过难对学生造成的心理负担,更多考查学生的基础性知识,帮助学生打好基础的根基后,再增加难度,搭建知识高楼.
高考命题需要调节好理解、应用与分析水平试题的比例,把握好合情推理与演绎推理的比例.可尝试在主观题中增加小题数量,考查水平由基础理解到问题分析,设置铺垫和引导,为学生完成全题创造条件.采用多选和填空题分两空的新题型,可增加中间得分,有效降低试卷整体难度.任子朝等人对新题型调查研究发现,师生对该类新题型的接受度较高,反响很好[15].这样可以改善数学考题给人的复杂和高难度的刻板印象,实现考题的有机均衡.
6.2 加强“整合” 体现综合性
在知识含量方面,法国单个知识点题目比重很大,而中国多个知识点的题目比例明显多于法国,即一道题考查多个知识点,注重知识间的交叉、渗透和整合.
2014年3月教育部印发的《关于全面深化课程改革落实立德树人根本任务的意见》提出“核心素养体系”,强调教学中将不同学段的相关内容整合到一起,组成大的知识群,结构化呈现[16].《2019年普通高等学校招生全国统一考试大纲——理科数学》中也着重突出了高考命题的综合性考查要求[17].
命题应与教学相辅相成,一题含多个知识点可以帮助学生在学习时构建完整的知识体系,培养学生的分析、总结与知识迁移能力.各章节内容独立,但又可以通过试题联系起来,体现知识的独立与统一.因而,在命题中应继续保证多知识点题目的数量与比例,在命题中体现出数学知识的综合性特点,帮助学生构建出完整、系统的知识体系.
6.3 注重“背景” 体现应用性
中国在背景因素方面无背景题目所占比例比较大,与法国形成鲜明对比.法国试题在命题上注重结合生活情境,科学背景题目占比也明显优于中国,看重对学生问题解决能力的培养与思维的开发.在考题与生活结合方面,中国近年来情况有所改善,如2019年中出现的“断臂维纳斯”,以此可以窥见全国卷试题与实际背景结合的命题改革方向,但有背景试题的数目与涉及的情境范围较之法国略显不足.
背景因素在数学学科的核心素养中有直接体现,表现形式为数学建模中的求解模型和检验结果.把现实抽象为数学,用数学解释现实.事实上,常磊和鲍建生通过对数学核心素养的具体分析表明:情境的设计直接影响对六大核心素养的有效评价[18].数学源于生活,又用于生活,背景因素的融入可以帮助学生提高应用意识,感受数学在实际生活中的价值,从而发现数学的魅力.
因此,在高考命题中,情境的融入可以围绕以下几个方面:(1)关注健康问题,比如可以结合2020年初出现的新型冠状病毒的传播与防治情况建立模型,通过感染概率、传播高峰等问题考查概率统计和函数知识;(2)关注自然资源,如结合人口数量变化、能源的供应问题来考查函数、优化、统计相关知识;(3)关注环境,比如结合垃圾分类与处理、气候的变化设计题目;(4)关注灾难,如地震预测原理的数学解释、战争中的运输优化问题;(5)关注科技前沿,如针对最新科技成果(比如5G、智能机器人、飞行模拟机、仿生鱼)中蕴含的基础数学知识合理改编来设置情境,在改编的同时要考虑到高中生的知识基础与认知水平,同时要考虑情境与考查知识的适切性,情境服务于知识的考查;(6)关注历史文化,如借助经典的“四色问题”“七桥问题”考查基础知识、结合中国古代优秀传统文化设计题目.也可以采取高等数学、竞赛数学知识来开阔学生视野,关注学科交叉体现数学实用性,对教材经典习题合理改编等手段来设计题目.
总之,命题情境在融合数学内容时,需要明确题目立意,合理设置目标任务;注意与数学素养的关联,考查学生数学素养的发展水平;恰当把握情境的复杂程度,考查不同层次的数学素养水平;合理建构真实的情境,排除与核心素养及知识无关因素的干扰.
6.4 关注“开放” 体现创新性
在过去的高考命题中,中国高考对开放性试题未作考查,而法国这方面的成果要优于中国.开放性试题给学生以自由发挥的空间,有利于培养学生积极思考、主动质疑的思维品质以及创新意识和能力,更符合当代社会的需要.
创新是民族的灵魂,党的十九大报告提出要建设创新型国家,培养创新型团队.中学阶段是培养创新思维与意识的关键时期,因此,高考命题中应有导向地培养学生创新意识,比如适当渗入一些需要学生做出判断的不确定性知识[19],开放性试题也可以成为其手段之一.
因此,在高考命题中,可以加入方法开放或是结果开放的试题[20],培养开放性思维.也可以设置创新型情境,让学生在情境中感知创新.或是从高等数学视角入手,登高望远,更好把握全局,也实现高考为高等教育培养人才的目的[21].
[1] 国务院.国务院关于深化考试招生制度改革的实施意见[J].人民教育,2014(18):16–19.
[2] 国务院办公厅.国务院办公厅关于新时代推进普通高中育人方式改革的指导意见[J].人民教育,2019(Z2):10–13.
[3] 教育部考试中心.2019年普通高等学校招生全国统一考试大纲[EB/OL].(2019–01–31)[2019–11–12].http://www. neea.edu.cn/res/Home/1901/86158689c683971ff0d198b6a80e5eb3.pdf.
[4] 张玉环,吴立宝,曹一鸣.法国初中数学教材特点剖析及启示[J].数学教育学报,2016,25(6):32–37.
[5] 何珊云.法国高中学业水平测试及启示[J].教育测量与评价,2010(7):49–53.
[6] 戴桂生.2006年法国中学毕业会考数学试卷(理科)[J].中学数学月刊,2007(7):43–44.
[7] 龚妙昆.2007年法国高中毕业会考(暨高等学校人学考)数学试题[J].数学教学,2008(11):46.
[8] 胡凤娟.主题式命题:来自法国数学高考试题的启示[J].中学数学教学参考,2019(25):74–78.
[9] 王冰,揭毅.基于综合难度系数模型的2018年高考地理试题评析[J].教育测量与评价,2018(12):40–48.
[10] 武小鹏,张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报,2018,27(3):19–24.
[11] Ministère de l’Education Nationale. Baccalauréat général session 2015—2019 mathématiques séries [EB/OL]. (2019–07–01) [2019–07–10]. https:// www.education.gouv.fr/examens-et-diplomes-41459.
[12] 王湖滨.PISA测试的“情境”及其带来的启示——大型国际教育评价项目对“情境”的述评[J].外国中小学教育,2014(1):8–14.
[13] 黄智华,渠东剑.高中生逻辑推理能力的调查研究——以南京市为例[J].数学通报,2018,57(6):28–33.
[14] 张斌,苟斌娥.基于核心概念的数学测评解析与教学建议——以重庆市2018年中考数学试题(A卷)为例[J].数学教育学报,2019,28(4):61–65.
[15] 任子朝,章建石,陈昂.高考数学新题型测试研究[J].数学教育学报,2015,24(1):21–25.
[16] 中华人民共和国教育部.关于全面深化课程改革落实立德树人根本任务的意见[EB/OL].(2014–03–30)[2019–11–12].http://www.jswxedu.com/html/jyfw/zgzj/190.html.
[17] 教育部考试中心.2019年普通高等学校招生全国统一考试大纲——理科数学[EB/OL].(2019–01–31)[2019–11–12].http://www.neea.edu.cn/res/Home/1901/d722242b1b7b3b4eed7d217dc782789a.pdf.
[18] 常磊,鲍建生.情境视角下的数学核心素养[J].数学教育学报,2017,26(2):24–28.
[19] 喻平.发展学生学科核心素养的教学目标与策略[J].课程·教材·教法,2017,37(1):48–53.
[20] 于涵,任子朝,陈昂,等.新高考数学科考核目标与考查要求研究[J].课程·教材·教法,2018,38(6):21–26.
[21] 张金良.高中数学创新题编制的几个入手处[J].中国数学教育,2019(18):11–17.
A Comparative Study of Chinese and French College Entrance Examination Mathematics Items (2015—2019): A Focus on Overall Difficulty——Based on the Chinese and French College Entrance Examination Mathematics Papers for 2015—2019
ZHANG Yu-huan, ZHOU Xia
(School of Mathematics and Statistics, Henan University, Henan Kaifeng 475004, China)
Since the launch of the reform of the college entrance examination in 2014 in China, the public has been increasingly concerned about the status of the reform and the quality of college entrance examination items. To understand the quality of the examination items, the Chinese college entrance examination items were analyzed from an international perspective. Qualitative and quantitative methods were used to analyze the examination items from the National Mathematics I for Natural-Science- Oriented Area in China and the French national baccalauréat exam (also known as the Graduation Examination) from 2015 to 2019. We analyzed both the overall difficulty of the examination items and conducted case studies. We draw on the reform requirements for the new Chinese college entrance examinations and ideas about developing students’ mathematical core competencies and make several suggestions for the improvement of college entrance examination items: The “transition” to the new examination items shall be a gradual process, and the items still need to pay attention to assessment of the basics; the examination items should increase the overall difficulty to assess students’ knowledge and thinking comprehensively; the examination items shall emphasize “situations” to assess applications of knowledge; and the examination items shall be “open-ended” to assess students’ innovativeness.
French mathematics; college entrance examination questions; comprehensive difficulty; comparative study
G40–059.3
A
1004–9894(2020)03–0043–08
2020–01–23
河南省2019年度教师教育课程改革研究项目——新手、熟手、专家型数学教师课堂教学行为的比较研究(2019-JSJYYB-005);河南大学2019年度本科教育教学改革研究与实践项目——数学师范类课程线上线下混合式教学的实践与研究(HDXJJG2019-20);河南大学研究生教育创新与质量提升计划项目——学科教学(数学)教学案例库建设和实践(SYL19040114)
张玉环(1983—),女,河南商丘人,副教授,博士,硕士生导师,主要从事数学教育、教师教育研究.
张玉环,周侠.综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷[J].数学教育学报,2020,29(3):43-50.
[责任编校:周学智、陈隽]
