基于最小二乘支持向量回归的划片刀刃长控制优化*

崔庆安， 段焕姣， 张 迪,， 乔 帅， 董 峰

(1. 郑州大学 管理工程学院， 郑州 450001)(2. 上海海事大学 经济管理学院， 上海 201306)(3. 郑州磨料磨具磨削研究所有限公司， 郑州 450001)

划片刀是集成电路、分立器件等半导体晶圆制造过程中进行切割与开槽的重要工具，主要由铝轮毂和刀刃等2部分组成，其中由金刚石磨料和镍基结合剂构成的刀刃是进行划切工作的主要部分，如图1所示。刀刃长度直接影响划片刀的使用性能：刀刃过长会导致刚度变差而引起切割缝蛇形弯曲；刀刃过短会导致使用寿命降低。因此，在划片刀的批量生产过程中，如何优化刀刃长度控制技术已成为重要的研究课题。

(a) 划片刀整体图Overall view of dicing blade(b) 划片刀剖视图Cutaway view of dicing blade 图1 划片刀结构图Fig. 1 Structure of dicing blade

现有研究大多是通过优化划片刀切割参数或某一质量特性等方式来提高划片刀的使用性能。李东亚等[1]对切削硅晶片用划片刀的车削工艺、电镀工艺和后续加工工艺进行研究，通过改变进刀速度优化了划片刀的切割参数；SU等[2]通过解决划片刀崩刃的关键问题，优化了划片刀的切割性能；YUAN等[3]以划片刀的径向磨损量、继电器电流、大于50 μm的切屑数量和最大切割尺寸作为试验参数进行试验，优化了划片工艺；尹韶辉等[4]通过单因素试验法研究了装夹紧固方式、划片刀种类、切割水流量对K9光学玻璃划切性能的影响。以上研究在一定程度上提高了划片刀的使用性能，但关于通过优化划片刀刃长控制技术，以优化划片刀使用性能的研究较少。

在划片刀生产工艺流程(图2)中，刀刃出露是控制刀刃长度的关键工序，且在连续生产中需要一次生产多片，片与片之间的刀刃长度存在波动性。因此，在相同工艺条件下，从批量生产的刀刃长度稳定性角度考虑，将刀刃出露工序的划片刀刃长极差作为响应，选取影响划片刀刃长控制的3个工艺参数作为影响因子进行试验，通过机器学习建模寻优实现划片刀刃长控制技术的优化。

图2 划片刀生产工艺流程图

考虑到试验复杂，选择了所需试验点少，且样本具有代表性的正交试验设计方式，同时选择适合小样本的最小二乘支持向量回归为建模方式进行研究。首先简单介绍正交试验设计和最小二乘支持向量回归的理论知识，然后给出刀刃出露工序中划片刀刃长控制优化分析的实现步骤，并输入工艺参数优化结果，验证工艺参数优化方法的有效性。

1 试验条件与方法

1.1 试验条件

试验用轮毂型电镀超薄金刚石划片刀，其厚度要求15～20 μm，刃长要求380～510 μm。刀刃出露过程是将已机械加工的23片划片刀串成1串，安装在带有旋转电机的主轴上，并将整串划片刀放入NaOH溶液中匀速旋转，通过腐蚀划片刀铝轮毂，最终使刀刃得以出露。使用带测量标尺的工业显微镜测量刀刃出露长度，每片圆周方向均等分测量3个点取平均值并记录。

1.2 正交试验设计

正交试验设计是一种常用的高效、快速、低成本的试验设计方法，可在多因子、多水平的全面试验中挑选出具有代表性的“关键点”[5]，形成新的试验集进行试验，所选择的点分布均衡[6]，比较适合成本较高或者试验结果不易取得的试验。

1.3 最小二乘支持向量回归

支持向量机(support vector machine，SVM)是基于统计学习理论提出的一种机器学习方法[7]，被认为是小样本建模和预测的最佳理论[8]。而SVM用于解决回归问题即为支持向量回归 (support vector regression，SVR)[9]，是通过有限样本集的学习来寻找最优超平面、建立近似模型，是一种基于结构风险最小化的非参数学习方法，不易在样本量较小时产生“过拟合”等问题[8]。

假设训练集为S0={(x1,y1), (x2,y2), … , (xN,yN)}，则对应的支持向量回归方程如式(1)所示：

f(x)=wT×φ(x)+b

(1)

式中：f(x)是理论回归方程;wT是权重向量;φ(x)是低维空间向高维空间映射的非线性函数;b是偏差值。

(2)

式中：n为训练集的样本量；xi为训练集中的参数向量；yi为对应的响应值；ε为随机误差。

最小二乘支持向量回归(least squares support vector regression，LS-SVR)是支持向量回归(SVR)的一种扩展[10]，通过将式(2)的不等式约束变为等式约束，在保留SVR优势的基础上，提高了求解效率。其表达式为：

(3)

式(3)的拉格朗日函数为：

b)-yi-ξi)

(4)

其中：αi为拉格朗日乘子。

对式(4)求偏导可得：

(5)

令α=[α1,…,αn]T，y=[y1,…,yn]T，Ω=[Ωij]n×n，Ωij=φ(xi)Tφ(xj)，则：

(6)

令Z=Ω+γ-1In，可得：

(7)

式中：1n=[1，1，…，1]T。

可得对应的LS-SVR回归方程为：

(8)

式中：k(xi,x)为核函数，可用来衡量样本之间的相似性。

1.4 划片刀刃长控制优化的算法设计

基于LS-SVR的划片刀刃长控制优化问题设计的基本思路为：首先，选择影响划片刀刃长控制的关键因子，根据正交设计获得试验方案；其次，依据试验方案进行试验，测量出各试验点对应子组中划片刀的刀刃长度，求出极差，形成响应样本集；再次，进一步对样本集进行LS-SVR建模，获得因子与响应的近似模型；最后采用粒子群算法对模型进行寻优，获得优化后的刀刃出露工艺参数与划片刀刃长极差。

2 试验设计

从划片刀刀刃出露工序的工艺参数中选择影响刀刃长度的溶液温度、溶液浓度、工件旋转速度3个因子作为试验因子进行试验。各因子及可行域见表1。

表1 试验因子及可行域

在可行域内，进一步对每个因子设置5个水平，具体见表2。依照L25(56)正交试验表安排试验。此正交表最多可安排6个因子，而本次试验只有3个因子，因此将3因子放在正交表6列的任选3列中，并将正交表中各列对应的水平序号换成具体水平，最终形成25组试验点。

表2 因子水平设置

3 算法实现

3.1 进行试验获得样本集

为了避免试验因子外的其他因子或试验区组对试验的影响，采用抽签的方式随机决定试验顺序，然后在25组试验点下再依次进行子组试验。在实际生产中每轮腐蚀23片，因此将子组的容量设置为23。划片刀试验样品制作完成后，在圆周方向3等分点测量刃长3次，取平均值作为刀刃长度值，测量结束后将子组刃长的极差作为响应，获得25组样本集，见表3。

3.2 利用样本集进行机器学习建立LS-SVR模型

3.3 模型寻优获得优化参数

在模型建立后，为寻找模型对应的最优参数值，选择粒子群算法实现寻优。粒子群算法(particle swarm optimization, PSO)的本质是一种随机搜索算法，该算法能以较大的概率收敛于全局最优，且参数较少，容易实现，与传统优化算法相比，具有较快的计算速度和更好的全局搜索能力。首先将粒子群算法工具箱放在目标路径下；其次利用Matlab编程，定义待优化的目标函数；最后调用PSO算法的核心函数，设置好初始参数，运行即可快速获得优化的溶液温度、溶液浓度、工件旋转速度3个工艺参数值与刃长极差值。

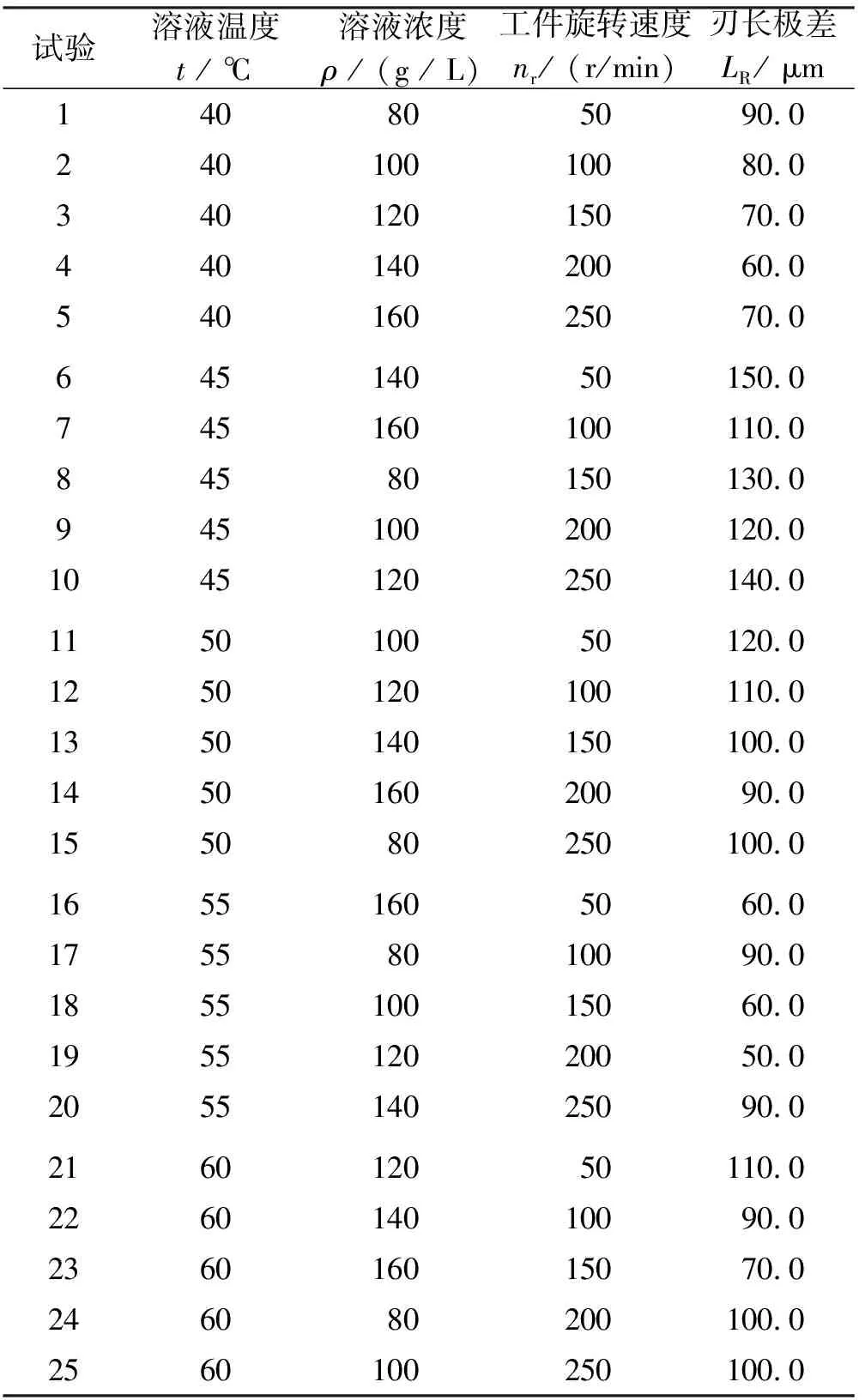
表3 样本集

3.4 验证并讨论参数优化的有效性

将工艺参数寻优的结果作为输入，进行3组重复试验，子组容量同样设置为23，求出每组刃长极差，取其平均值为试验验证结果，见表4。

表4 建模寻优结果与实际试验结果对比

从表4可以看出：在溶液温度为55.4 ℃，溶液浓度为114.8 g/L，工件旋转速度为184 r/min的工艺条件下，建模的最优刃长极差为46.2 μm；而在实际验证中，3个子组的刃长极差分别为50.0、47.0、48.0 μm，均值为48.3 μm。二者的差值较小，仅为2.1 μm，验证了建模确定最优刃长极差的可行性。

4 结论

针对划片刀刀刃出露工序批量生产中刀刃长度波动性的问题，将生产工艺过程中同一子组的刃长极差作为响应，选取影响刃长的溶液温度、溶液浓度、工件旋转速度3个关键因子，进行正交试验设计，并采用最小二乘支持向量回归建立模型，进一步利用粒子群算法对模型寻优，实现了划片刀刀刃出露工序刀刃长度稳定控制技术的优化，实际验证试验结果和建模寻优结果的划片刀刃长极差的差值仅为2.1 μm，验证了利用建模确定最优刃长极差的可行性。