考虑密封垫表面工作状态的盾构隧道接缝防水能力数值模拟研究

张亚洲

(上海市政工程设计研究总院(集团)有限公司， 上海 200092)

0 引言

随着城市建设的快速推进及交通需求的增加，我国盾构法施工隧道不断朝大直径、高水压方向发展[1-3]。因盾构隧道由预制管片逐块、逐环拼装而成，管片块间、环间存在大量接缝，使得接缝防水问题已成为制约盾构隧道技术发展的重要因素。目前我国的管片接缝防水构造中，三元乙丙橡胶(EPDM)弹性密封垫是最重要、最常用的防水材料，其主要依靠橡胶密封垫的弹性压密，以接触面的表面接触应力来止水。弹性密封垫生产出厂后，运输至盾构隧道施工现场，经临时存放、槽口粘贴、随管片下井拼装直至其发挥防水作用，整个过程中诸多环节都影响密封垫表面工作状态，成为密封垫防水能力的影响因素。

当前国内外对接缝弹性密封垫防水能力的研究方法主要有试验研究和数值模拟。文献[4-10]结合实际工程对接缝的防水性能要求，对弹性密封垫进行了一字缝、T字缝防水试验和闭合压缩力试验。文献[11-16]基于不可压缩橡胶材料Mooney-Rivlin本构模型，利用数值分析软件对弹性密封垫在不同形状及压缩量下的变形特征、接触面应力分布及压缩力进行数值模拟分析，取得了大量研究成果。在考虑弹性密封垫工作状态上： 刘建国等[17]对密封垫防水机制进行阐述，对孔壁失稳与闭合压缩的过程及孔洞气囊效应进行探索；孙廉威[18]建立弹性密封垫受水压作用下的数值模型，对弹性密封垫在不同张开量下的防水性能、接触应力分布以及防水失效模式进行研究，提出基于施加水压的防水性能评价方法。

目前在密封垫的试验及数值模拟研究中，普遍忽略了密封垫表面工作状态，如： 密封垫底部与管片粘接状态、密封垫顶面涂抹水性润滑剂状态、弹性密封垫沾水浸湿状态等。本文以上述学者的研究为基础，结合现场施工时出现的多种工况，建立弹性密封垫数值计算模型，探讨密封垫多种表面工作状态下的防水能力。

1 密封垫施工过程及表面工作状态分析

1.1 密封垫施工过程

依据设计断面形式，弹性密封垫在工厂由三元乙丙橡胶挤出硫化成型后，加工成棱角分明的框形，环、纵向尺寸与管片防水槽口尺寸相匹配。通常情况下，弹性密封垫经生产至随管片拼装就位发挥防水作用，会经过如下几道施工工序：

1)密封垫运输及存储。批量的框形弹性密封垫运输至施工现场暂时存储。

2)管片防水槽口清理。采用铲刀、毛刷及稀释剂等清除管片防水槽口表面的泥沙、粉尘、浮浆、水渍、油污等杂质。

3)密封垫粘贴。将框形密封垫套在管片上，在密封垫底面及防水槽口涂刷胶黏剂；采用四角定位法将密封垫粘贴在防水槽内，并用橡胶锤击打密封垫，使其粘贴牢固。

4)涂刷润滑剂。为减少封顶块管片插入时弹性密封垫间的摩擦阻力，封顶块与邻接块两侧防水密封垫在拼装前涂表面润滑剂。

5)养护及下井拼装。养护12 h后，随管片下井至盾尾拼装就位，在千斤顶顶压(环缝)或管片自重(纵缝)作用下压实，经螺栓初拧、复拧后，相邻两密封垫产生接触应力。

6)在隧道后续施工及正常运营期间发挥防水作用。

1.2 密封垫表面工作状态影响因素

根据1.1节分析可知，密封垫表面工作状态存在以下影响因素：

1)密封垫粘贴质量难以控制。潮湿的基层表面、界面清理不佳，粘结剂涂刷不饱满，养护时间不够等均无法保证管片密封垫的粘贴质量。

2)根据弗雷克利等[19]的研究成果，干燥状态的橡胶具有很高的摩擦因数，但当橡胶用水湿润后其摩擦大大降低。对于封顶块及邻接块接缝，密封垫顶面摩擦状态受水性润滑剂涂刷情况影响，当涂抹水性润滑剂后，摩擦性能降低显著。对于标准块接缝，密封垫摩擦状态受施工时的天气状况、拼装时是否浸水等情况的影响。

3)密封垫随管片拼装就位后，迎水面直接与水接触，背水面暂时处于干燥状态，随着隧道长期沉降、变形及水的缓慢渗透作用，密封垫表面及内部可能受潮，从而影响工作状态。

基于上述分析，本文建立密封垫有限元数值计算模型，重点研究密封垫底部粘贴、顶部涂抹润滑剂及沾水湿润等状态的影响，并讨论长期工作状态下的密封垫防水能力。

2 数值计算方法构建密封垫槽口和弹性密封垫

2.1 有限元模型

根据图1所示密封垫槽口和弹性密封垫断面形式建立相应的二维有限元模型[18]。模型中混凝土密封垫槽口采用刚体进行模拟，弹性密封垫则采用实体单元进行模拟。网格采用四边形单元，共划分3 214个单元。弹性密封垫有限元网格划分如图2所示。

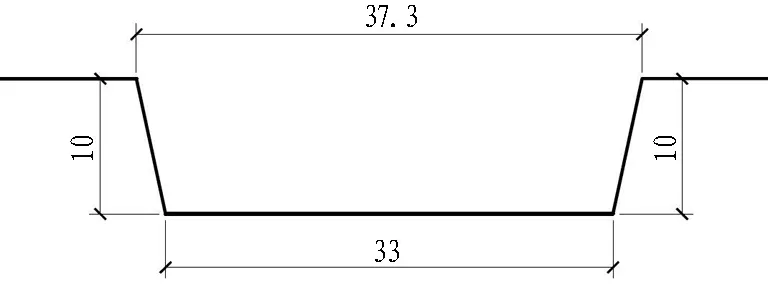
(a) 防水槽口断面

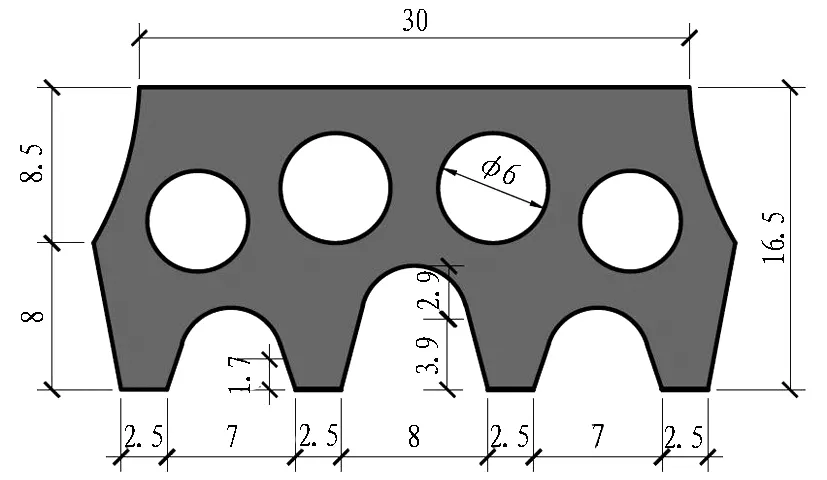
(b)密封垫断面形式

Fig. 1 Cross-sections of waterproof notch and sealing gasket (unit: mm)[18]

图2 弹性密封垫有限元网格

2.2 工作状态设定

根据上文密封垫表面工作状态的分析，将密封垫分为顶面U、底面D、外侧(迎水面)O、内侧(背水面)I以及内孔C 5个区域，如图3所示。

图3 密封垫分区示意图

根据具体工况的不同，模拟密封垫与槽口之间及密封垫自身的相互作用(绑定或接触)。绑定约束(TIE)将2个区域进行绑定，防止发生分离或相对滑动。接触作用设定为法向硬接触，切向采用罚接触，切向摩擦因数根据情况设定，且允许接触分离。

图4为相互作用设置示意图,设定主要原则如下：

1)对于顶面U涂抹水性润滑剂的情况，考虑润滑剂润滑作用，设定上、下密封垫间接触摩擦因数为0.1。密封垫干燥状态时，摩擦因数设定为0.5[15, 18]；沾水时考虑摩擦因数的降低[19]，设定为0.25，如图4(a)所示。

2)对于底面D，若考虑粘贴作用，密封垫8个梳形齿底部与槽口间设置为绑定(TIE)作用，如图4(b)T1～T8所示； 底部开放孔与槽口间及底部开放孔自身接触摩擦因数为0.5，如图4(c)和4(d)所示。若不考虑粘贴作用，密封垫底部与槽口间接触摩擦因数及密封垫底部自接触的摩擦因数根据是否沾水分别设定为0.25、0.5，如图4(h)和4(i)所示。通常，水性润滑剂在密封垫已牢固粘贴于槽口后涂抹，故不考虑密封垫底部接触摩擦因数为0.1的工况。

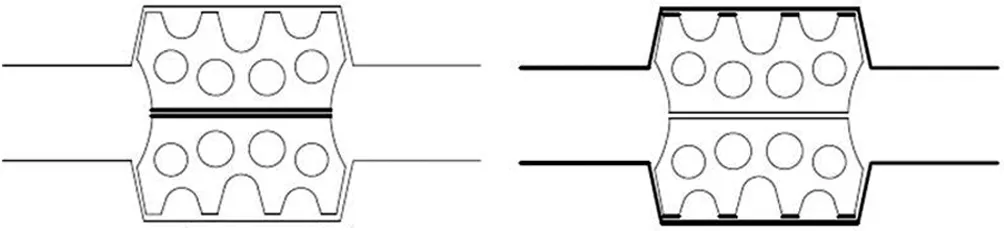
(a) 密封垫顶面接触U (b) 密封垫底部绑定T1～T8

(c) 密封垫底部与槽口接触 E1～E6 (d) 密封垫底部自接触E7～E12

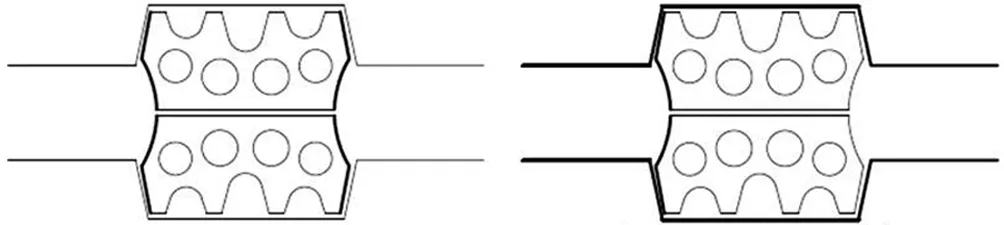
(e) 密封垫内、外侧自接触I1、I2、O1、O2(f) 密封垫外侧与槽口接触O3～O6

(g) 密封垫内侧与槽口接触I3～I6 (h) 密封垫底部与槽口接触D1、D2

(i) 密封垫底部自接触D3、D4 (j) 密封垫内孔自接触C1～C8

图4相互作用设置示意图

Fig. 4 Interaction settings

3)对于外侧(迎水面)O、内侧(背水面)I，考虑过量涂抹水性润滑剂工况、干燥工况及沾水工况，接触摩擦因数分别设定为0.1、0.5、0.25，如图4(e)—(g)所示。

4)对于内孔C，根据长期高水压工作下水是否浸润，其接触摩擦因数分别设定为0.25、0.5。实际施工时，涂抹于密封垫表面水性润滑剂较少，不会渗透入内孔中，故内孔不存在接触摩擦因数为0.1的工况，如图4(j)所示。

为研究上述不同相互作用组合情况对密封垫防水能力的影响，设定A1—A14共计14项计算工况，各计算工况的接触条件如表1所示。

表1 计算工况的接触条件

注： 数值为摩擦因数。

2.3 材料本构及计算参数

橡胶材料应力与应变之间的非线性关系主要通过应变能函数来定义。对于盾构隧道防水用三元乙丙橡胶密封垫，工程上通常采用Mooney-Rivlin模型来模拟，该模型需明确C01与C102个密封垫参数。基于橡胶材料的不可压缩性，其泊松比μ=0.5，弹性模量E、剪切模量G及泊松比μ与密封垫计算参数C10、C01之间关系如下：

(1)

Gent[20]采用理论分析后建议橡胶材料Mooney-Rivlin本构模型材料参数：C10=4C01，G=10C01。

通常采用试验将对C10、C01的确定转化为对E或G的确定。在不进行试验的情况下，可根据E或G与橡胶硬度的关系来确定，目前文献中常见以下3种计算公式。

E=(15.75+2.15HA)/(100-HA)。

(2)

式中HA为邵尔硬度[20-21]。

G=0.086×1.045H。

(3)

式中H为橡胶硬度[15, 22]。

郑明军等[23]根据弗雷克利等[19]提出的橡胶材料IRHD硬度Hr与E的试验数据拟合得到

lgE=0.019 8Hr-0.543 2。

(4)

目前，我国大直径盾构隧道三元乙丙弹性橡胶密封垫指标要求多采用邵尔(Shore)A硬度指标，式(4)采用的国际硬度(IRHD)指标不适用。硬度HA范围值多为60～70，采用式(2)和式(3)计算得到的C01、C10均相差不到1.5%，相差很小。本文采用式(2)，取三元乙丙橡胶硬度值为65，代入式(2)得C01=0.148 MPa，C10=0.592 MPa。

2.4 边界条件及荷载工况

在本文计算中，密封垫槽口采用刚体进行模拟，初始边界条件为： 在下部槽口的参考点2处(见图2)约束其竖向、侧向和转动位移；在上部槽口的的参考点1处约束其侧向和转动位移，利用其竖向位移使弹性密封垫进行压缩。

弹性密封垫压缩后，会在其与槽口及密封垫间的接触面处产生接触应力。由于弹性密封垫间的接触应力分布是不均匀的，通常密封垫的防水能力介于平均接触应力和最大接触应力之间。为简化考虑，从安全角度出发，本文采用密封垫顶部接触面的平均接触应力评价密封垫的防水能力。

2.5 模型验证

孙廉威[18]采用有限元软件对图1所示的弹性密封垫进行了压缩情况下的接触应力分析，得到了弹性密封垫在张开6 mm时的密封垫顶面接触应力分布，如图5中蓝线所示。为了验证本文建立的模型的合理性，提取本文模型(工况A14)计算得到的在张开6 mm时的密封垫顶面接触应力，如图5中红线所示。

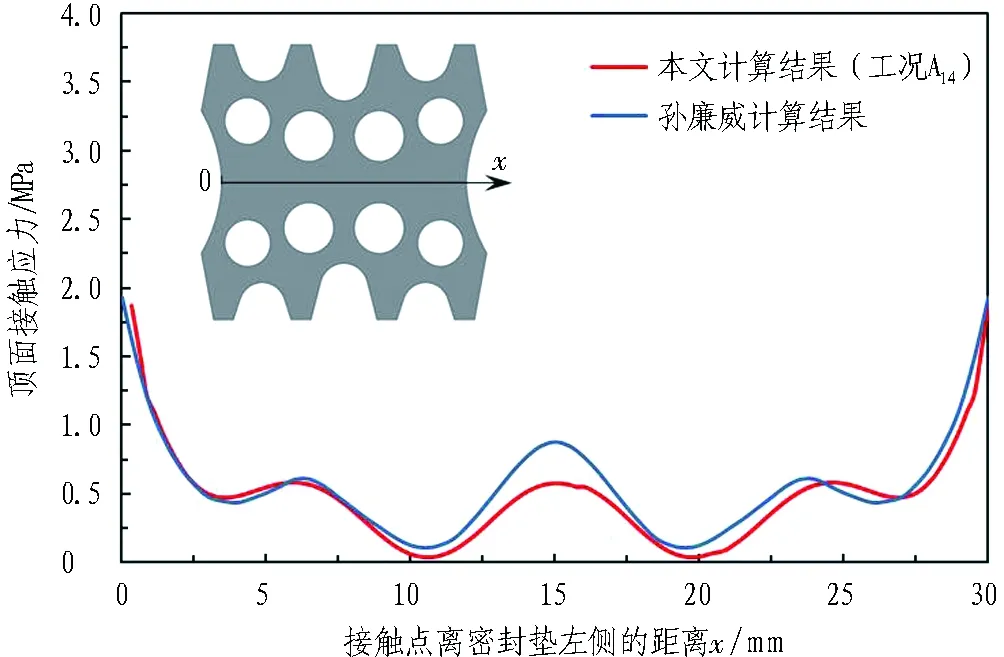
图5 本文模型与孙廉威[18]计算模型结果比较

从图5中可以看出，用本文模型计算得到的接触应力与孙廉威[18]计算结果在趋势上吻合较好，具体数值稍有差异，但总体差异不大，这主要是由于密封垫计算参数(C01、C10)选取有所区别。这在一定程度上验证了本文模型的合理性，为后续分析弹性密封垫在不同表面工作状态下的防水能力分析奠定了基础。

2.6 考虑密封垫表面状态的计算与常规计算对比

表1所示计算工况中，工况A1及A14为目前文献中最常见的2种计算方式： A1仅考虑了密封垫底部与槽口的粘贴(TIE)作用，未考虑顶部润滑作用、雨水浸润状态；A14为密封垫干燥状态，不考虑密封垫底部与槽口的粘贴作用、顶部润滑作用、雨水浸润状态。A3为考虑密封垫表面工作状态(顶面涂润滑剂、底面与槽口粘贴、外侧临水湿润、内侧干燥)的计算工况。A1、A14、A33种工况计算结果如图6所示。

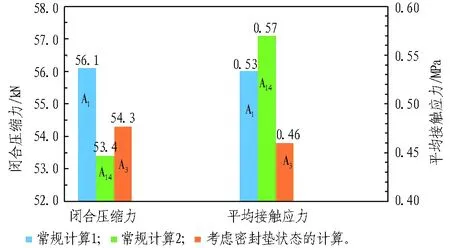
图6 考虑密封垫表面状态的计算与常规计算结果对比

Fig. 6 Comparison between calculation results considering gasket surface conditions and conventional calculation results

由图6可知，是否考虑密封垫表面工作状态对计算结果有一定影响，闭合压缩力误差相对较小(约为3.3%)，平均接触应力误差相对较大(约为23.9%)，考虑密封垫表面工作状态的平均接触应力小于常规方法的计算结果。因此，采用常规方法计算平均接触应力评价密封垫防水能力时，可能存在不安全因素，而考虑密封垫表面工作状态的计算则较为安全、合理。

3 密封垫表面工作状态的影响

3.1 密封垫底部粘贴效应的影响

为考虑底部粘贴效应的影响，选取3组具有单一变量的对比工况组(即A3与A6，A4与A7，A5与A8)，计算得到的闭合压缩力及平均接触应力如图7和图8所示。

由图7和图8可知，考虑密封垫底部粘贴效应的闭合压缩力及平均接触应力均大于不考虑底部粘贴效应时的结果，其中闭合压缩力的影响值范围为3.1%～19.9%，平均接触应力影响值范围为0～24.5%。这主要是因为粘贴剂的约束，密封垫在压缩过程中脚部不易“失稳”、“倾倒”，且底部粘贴效应约束了密封垫底部的横向变形，一定程度上增大了双向受压效应，使接触面应力、闭合压缩力更大，防水更可靠，如图9(a)所示；而不考虑粘贴剂作用时，由于脚部在约束过程中容易“失稳”、“倾倒”，且横向约束作用较弱，使得接触面应力、闭合压缩力更小,如图9(b)所示。

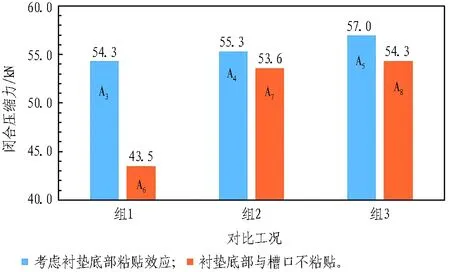
图7 密封垫底部粘贴效果对闭合压缩力的影响

Fig. 7 Influence of sticking effect at bottom of gasket on closed compression force

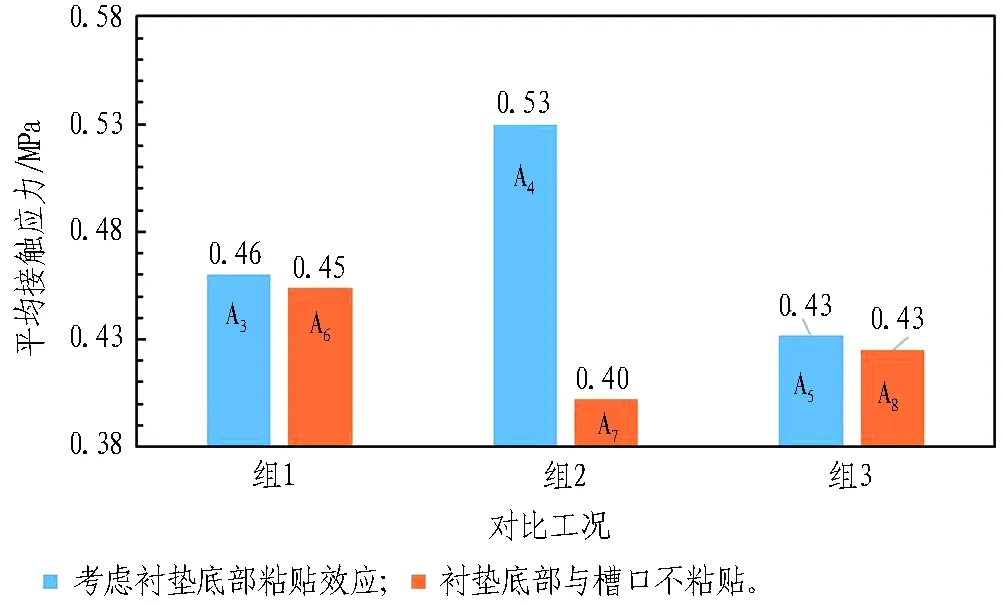
图8 密封垫底部粘贴效果对平均接触应力的影响

Fig. 8 Influence of sticking effect at bottom of gasket on average contact stress

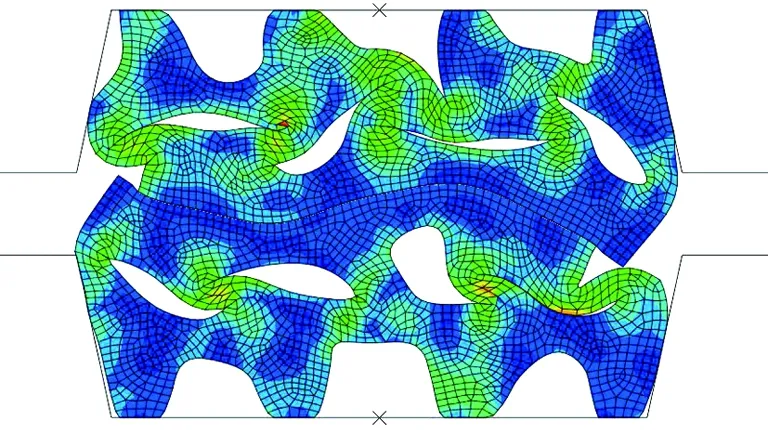
(a) 底部粘贴状态下张开量为5 mm时的变形应力状态

(b) 底部未粘贴状态下张开量为5 mm时的变形应力状态

Fig. 9 Influence of sticking effect at bottom of gasket on gasket deformation

3.2 水性润滑剂的影响

为研究密封垫顶部是否涂抹水性润滑剂的影响差别，选取3组具有单一变量的对比工况组(即A3与A5，A6与A8，A9与A11)，计算得到的闭合压缩力及平均接触应力如图10和图11所示。为考虑密封垫顶部润滑剂涂抹过量工况，另将A2组计算结果列出。

图10 密封垫顶部涂抹润滑剂对闭合压缩力的影响

Fig. 10 Influence of painting gasket top with lubricant on closed compression force

图11 密封垫顶部涂抹润滑剂对平均接触应力的影响

Fig. 11 Influence of painting gasket top with lubricant on average contact stress

由图10和图11可知，密封垫顶部涂抹润滑剂能够减小闭合压缩力、增加接触面平均接触应力，影响值范围为4.7%～19.9%、6.5%～11.1%。同时，由工况A2与A3的对比可知，润滑剂涂抹过量对闭合压缩力及平均接触应力影响较小，主要原因在于本文设定的润滑剂涂抹过量工况考虑在密封垫前、后两面，在密封垫压缩过程中接触面积小，因而影响较小。

3.3 密封垫沾水的影响

密封垫施工过程中，由于保存不当、不文明施工等情况，导致密封垫沾水，如： 雨中施工或仰拱块浸在盾构拱底水中，密封垫底部与槽口粘贴效果不佳，但密封垫顶部的水性润滑剂仍能发挥正常作用，即表1中A13所示工况。工况A13计算结果与正常施工工况A3的计算结果如图12所示。

由图12可知，表面沾水时，密封垫闭合压缩力由54.3 kN变为38.5 kN，降低29.1%；接触面平均接触应力由0.46 MPa降低至0.42 MPa，降低8.7%。

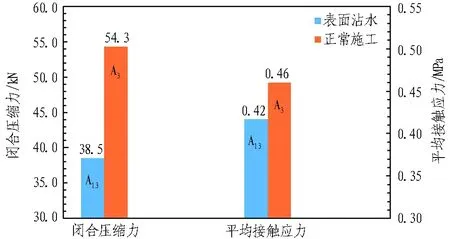
图12 表面沾水对闭合压缩力及平均接触应力的影响

Fig. 12 Effect of wet surface on closed compressive force and average contact stress

3.4 长期工作状态下的防水能力分析

通常情况，密封垫粘贴于管片槽口、顶部涂抹润滑剂，随管片拼装就位后，迎水面直接与水接触，背水面暂时处于干燥状态(A3工况)；随着隧道长期沉降、变形，密封垫在高应力及水的缓慢渗透作用下，密封垫表面润滑剂逐渐消失(A5工况)，密封垫表面可能受水浸润(A4)，密封垫底部粘贴作用逐渐失效(A7、A10)，内部封闭孔洞受潮(A12)，其表面工作状态一直处于动态变化中。因此，将上述密封垫表面工作状态发展的各阶段平均接触应力计算结果列出，如图13所示。

图13 平均接触应力随密封垫工作状态发展的变化

Fig. 13 Development of average contact stress with working state of gasket

由图13可知，在长期工作情况下，由于密封垫表面接触状态的不断变化，密封垫平均接触应力整体呈下降趋势，由初始的0.46 MPa下降至最终的0.35 MPa，下降约23.9%。值得说明的是，由于管片一开始已拼装就位、密封垫开始发挥防水作用，分析长期工作状态下的闭合压缩力意义不大，故本次未计算。

4 结论与建议

1)是否考虑密封垫表面工作状态的闭合压缩力、平均接触应力计算结果差异分别为3.3%、23.9%，评价密封垫防水能力时应考虑密封垫表面工作状态。

2)由于粘贴效应约束了密封垫底部的横向变形，且脚部不易失稳、倾倒，考虑密封垫底部粘贴效应的闭合压缩力及平均接触应力计算结果均大于不考虑底部粘贴效应时的计算结果，影响值范围分别为3.1%～19.9%、0～24.5%。密封垫顶部涂抹润滑剂能够减小闭合压缩力、增加接触面平均接触应力，影响值范围分别为4.7%～19.9%、6.5%～11.1%。表面沾水时，密封垫闭合压缩力降低29.1%；接触面平均接触应力降低8.7%。

3)在长期工作情况下，由于密封垫表面接触状态的变化，密封垫平均接触应力整体呈下降趋势，最终下降约23.9%。

4)本文仅从理论上分析了密封垫表面工作状态对防水能力的影响，忽略了密封垫表面状态所导致的施工质量缺陷。如： 在实际工程中，若密封垫粘贴不牢或表面沾水，将导致密封垫脱落从而形成直接的渗水通道；封顶块不涂润滑剂，将导致密封垫挤出、拉断或堆叠，导致闭合压缩力过大、防水失效等问题。

参考文献(References)：

[1] 朱祖熹. 盾构隧道管片接缝密封垫防水技术的现状与今后的课题[J]. 隧道建设, 2016, 10(36): 1171.

ZHU Zuxi. State-of-art and developing direction of waterproofing technology for sealing gasket of shield tunnel segment joints [J]. Tunnel Construction, 2016, 10(36): 1171.

[2] 张亚洲, 夏鹏举, 魏代伟, 等. 南京纬三路过江通道泥水处理及全线路废弃土再利用技术[J]. 隧道建设, 2015, 35(11): 1229.

ZHANG Yazhou, XIA Pengju, WEI Daiwei, et al. Slurry treatment and waste muck recycling use in construction of Weisanlu Yangtze River crossing tunnel in Nanjing[J]. Tunnel Construction, 2015, 35(11): 1229.

[3] 朱伟, 闵凡路, 姚占虎, 等. 盾构隧道开舱技术现状及实例[J]. 现代隧道技术, 2015, 52(1): 9.

ZHU Wei, MIN Fanlu, YAO Zhanhu, et al. Technical status and case study on intervention in the shield chamber[J]. Modern Tunnelling Technology, 2015, 52(1): 9.

[4] LI Xue, ZHOU Shunhua, DI Honggui, et al. Evaluation and experimental study on the sealant behaviour of double gaskets for shield tunnel lining[J]. Tunnelling and Underground Space Technology, 2018, 75: 81.

[5] GIRNAU G. Lining and waterproofing techniques in Germany[J]. Tunnels and Tunnelling International, 1978, 10(3): 36.

[6] SHALABI F I. Behavior of gasketed segmental concrete tunnel lining[D]. Urbana: University of Illinois, 2001.

[7] 陆明, 雷震宇, 张勇, 等. 上海长江隧道衬砌接缝和连接通道的防水试验研究[J]. 地下工程与隧道, 2008(4): 12.

LU Ming, LEI Zhenyu, ZHANG Yong, et al. Waterproofing test of lining joint and cross passage of Shanghai Yangtze River Tunnel[J]. Underground Engineering and Tunnels, 2008(4): 12.

[8] 赵运臣, 肖龙鸽, 刘招伟, 等. 武汉长江隧道管片接缝防水密封垫设计与试验研究[J]. 隧道建设, 2008, 28 (5): 570.

ZHAO Yunchen, XIAO Longge, LIU Zhaowei, et al. Experiment study and design on the watertight seal for reinforced concrete segment joint of Wuhan Yangtze River Tunnel[J]. Tunnel Construction, 2008, 28(5): 570.

[9] 何太洪, 周冠南, 刘训华, 等. 杭州地铁1号线越江隧道管片防水密封垫优化研究[J]. 地下工程与隧道, 2009(增刊): 41.

HE Taihong, ZHOU Guannan, LIU Xunhua, et al. Optimization of elastic gasket of Hangzhou Metro Line 1 cross-river tunnel[J]. Underground Engineering and Tunnels, 2009(S): 41.

[10] 丁文其, 赵伟, 彭益成, 等. 盾构隧道防水密封垫长期防水性能预测方法研究[C]//水下隧道建设与管理技术论文集. 北京: 中国公路学会, 2013： 20.

DING Wenqi, ZHAO Wei, PENG Yicheng, et al. Long term waterproof performance of shield tunnel sealing gasket[C]//Proceedings of construction and management technology of underwater tunnel. Beijing: China Highway & Transportation society, 2013： 20.

[11] 向科, 石修巍. 盾构管片弹性密封垫断面设计与优化[J]. 地下空间与工程学报, 2008, 4(2): 361.

XIANG Ke, SHI Xiuwei. Design and optimization of elastic gasket section of shield tunnel lining[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(2): 361.

[12] 罗驰, 雷震宇. 孔洞排布型式对盾构隧道橡胶密封垫的受力差异及稳定性分析[J]. 城市轨道交通研究, 2015, 18(5): 44.

LUO Chi, LEI Zhenyu. Stress difference and stability of shield tunnel rubber sealing gasket induced by different hole arrangements[J]. Urban Mass Transit, 2015, 18(5): 44.

[13] 雷震宇. 盾构隧道管片橡胶密封垫的优化设计方法[J]. 地下空间与工程学报, 2010, 6(4): 770.

LEI Zhenyu. An optimal design approach for the rubber sealing gasket in shield tunneling[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(4): 770.

[14] 王湛. 水下盾构隧道弹性密封垫防水失效数值模拟研究[J]. 隧道建设, 2015, 35(11): 1164.

WANG Zhan. Numerical study on waterproof failure mechanism of elastic sealing gasket of underwater shield-bored tunnel[J]. Tunnel Construction, 2015, 35(11): 1164.

[15] 曾格华, 梅宇. 防水失效的盾构隧道管片环收敛变形控制标准研究[J]. 路基工程, 2017(1): 53.

ZENG Gehua, MEI Yu. Research on control criteria of convergence and deformation for the waterproofing and failed shield tunnel segment ring[J]. Subgrade Engineering, 2017(1): 53.

[16] 龚琛杰, 丁文其. 大直径水下盾构隧道接缝弹性密封垫防水性能研究: 设计方法与工程指导[J]. 隧道建设(中英文), 2018, 38(10): 1712.

GONG Chenjie, DING Wenqi. Waterproof properties of elastic sealing gaskets used in segmental joints of large-diameter underwater shield tunnels: Design methodology and engineering guidance[J]. Tunnel Construction, 2018, 38(10): 1712.

[17] 刘建国, 周顺华. 考虑气囊效应的盾构隧道密封垫压缩性能分析[J]. 建筑材料学报, 2013, 16(6): 993.

LIU Jianguo, ZHOU Shunhua. Analysis of the performance of the shield tunnel gasket compression considering the balloon effect[J]. Journal of Building Materials, 2013, 16(6): 993.

[18] 孙廉威. 基于施加水压的盾构接缝防水机制数值分析[J]. 隧道建设(中英文), 2018, 38(4): 603.

SUN Lianwei. Numerical analysis of waterproof mechanism of shield tunnel joint based on applied water pressure[J]. Tunnel Construction, 2018, 38(4): 603.

[19] 弗雷克利 P K, 佩恩 A R. 橡胶在工程中应用的理论与实践[M]. 杜承泽, 唐宝华, 罗东山, 等译. 北京: 化学工业出版社, 1985.

FREAKLEY P K, PEIN A R. Theory and practices of engineering with rubber[M]. Translators: DU Chengze, TANG Baohua, LUO Dongshan, et al. Beijing: Chemistry Industry Press, 1985.

[20] GENT A N. Engineering with rubber: How to design rubber components[M]. 2nd ed. Munich: Hanser Publisher, 2001.

[21] 王伟, 邓涛, 赵树高. 橡胶 Mooney-Rivlin 模型中材料常数的确定[J]. 特种橡胶制品, 2004, 25(4): 8.

WANG Wei, DENG Tao, ZHAO Shugao. Determination for material constants of rubber Mooney-Rivlin model[J]. Special Purpose Rubber Products, 2004, 25(4): 8.

[22] BATTERMANN W, KÖHLER R. Elastomeric suspension, elastic bearing: Basics engineering calculation and construction[M]. Berlin: W Ernst, 1982.

[23] 郑明军, 王文静, 陈政南, 等. 橡胶Mooney-Rivlin 模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8): 462.

ZHENG Mingjun, WANG Wenjing, CHEN Zhengnan, et al. Determination for mechanical constants of rubber Mooney-Rivlin model[J]. China Rubber Industry, 2003, 50(8): 462.