矩形巷道围岩弹性变形能积聚特征分析1)

2020-07-02杨丹刘洋

力学与实践 2020年3期

杨丹刘洋

∗(大同煤炭职业技术学院，山西大同037000)

†(中煤能源研究院有限责任公司，西安710054)

随着浅部煤炭资源逐渐枯竭，煤炭资源开发不断走向地球深部(我国约53%的煤炭资源埋深超过1000 m)，千米深井的深部煤炭资源开采逐渐成为煤炭资源开发新常态。然而，进入深部开采，煤炭资源赋存的地质条件复杂、地应力增大、煤岩体破裂程度加剧等因素带来煤矿冲击地压等动力灾害更加严重。而我国目前的煤矿冲击地压主要发生在巷道中[1-3]，其主要原因之一就是巷道围岩积聚了大量的弹性能。因此，巷道围岩弹性变形能积聚特征研究对降低巷道支护成本和防治巷道冲击地压具有重要的科学意义和应用价值。

近年来，随着我国矿井进入深部开采，在应力等作用下巷道稳定性越来越低，危险性越来越高[4-7]。理论与实践表明，若要全面准确地认知巷道围岩的结构特征及应力影响范围，对其进行有效控制，预防围岩变形、破坏，同时保证巷道围岩稳定性，必须掌握巷道围岩能量积聚特征，这是地下工程急需解决的基础课题。目前，国内外学者针对巷道围岩的结构及其影响范围进行了大量研究，李铀等[8]应用塑性力学进行了圆形巷道破损区、地层残余强度等方面的研究；侯公羽等[9]使用水泥砂浆矩形巷道围岩试件模拟矩形巷道在不同开挖卸荷速率条件下的变形规律和声发射特性研究；李为腾等[10]以赵楼煤矿巷道为工程背景，开展地质力学模型试验，研究深部厚顶煤巷道围岩变形破坏特性及其机制；袁亮等[11]针对淮南矿区深部岩巷围岩的复杂赋存条件，提出淮南矿区深部围岩稳定控制的技术措施体系及施工安全控制的成套技术；李树忱等[12]利用Hamilton 时域变分原理，得出隧道围岩体扰动应力、应变和位移的解答函数式；董春亮等[13]针对深部高地应力条件下巷道开挖，基于弹性卸荷理论，运用留数定理和拉氏逆变换的延滞性给出动态开挖卸荷应力解析解；谢良涛等[14]采用数值模拟方法，验证了不同开挖方式下围岩应变能积聚对岩体损伤区及岩爆孕育的影响。而巷道断面尺寸、采深及煤层厚度等对巷道围岩弹性能积聚影响的研究还不够深入，因此，针对巷道围岩能量积聚特征开展研究具有重要的工程意义。

1 巷道冲击破坏失稳能量准则建立

巷道冲击地压是巷道周围煤岩体能量突然、瞬间释放过程。巷道周围煤岩体释放能量主要来源于震源传递到巷道的能量和巷道围岩弹性变形积聚能量[2]。

如震源初始能量为Ez，震源到巷道中心的距离为d，震源与巷道中心两点连线与巷道边界交点到巷道中心距离为r，震动波在煤岩中传播的能量衰减指数为η。则巷道周围煤岩体来源于震源传递到巷道的释放能量Ezh为

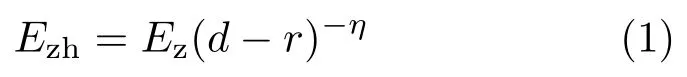
巷道围岩在原岩应力场中积聚的弹性变形能为

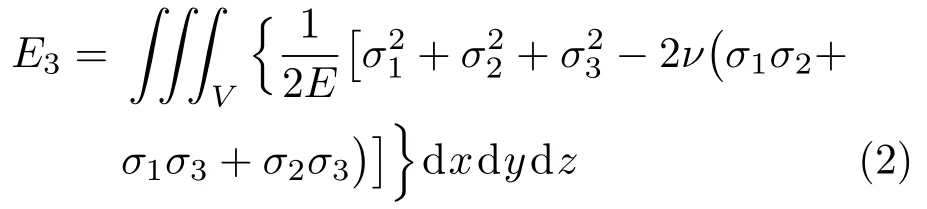
巷道开挖过程中岩体的塑性变形、围岩节理面间相对滑移等会产生部分能量耗散。一旦巷道围岩破坏启动，煤岩体受力迅速由三向变为单向。根据能量转移遵循最小能量原理，煤岩体破坏所需能量为单向应力状态下的破坏能量，即最小破坏能量Emin为

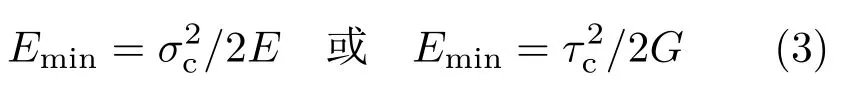
则巷道周围煤岩体来源于巷道围岩弹性变形积聚释放能量Ep为

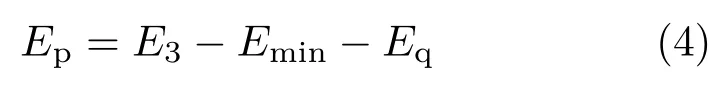
由式(1)和式(4)可得冲击地压发生时，巷道周围煤岩体释放能量

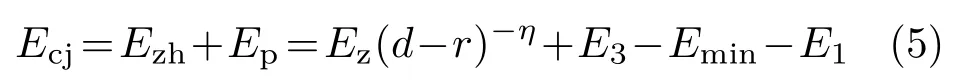
冲击地压发生时，巷道周围煤岩体释放能量一部分被巷道支护结构吸收，另一部分以煤岩动能形式向巷道释放。

假设在围岩压力下，巷道支护结构最大变形量为δ，巷道支护结构能承受冲击载荷为Fzf，则巷道支护结构弹性变形吸收能量为

假设冲击地压发生时，以煤岩动能形式向巷道释放的能量为Ez。

根据能量守恒定律可得

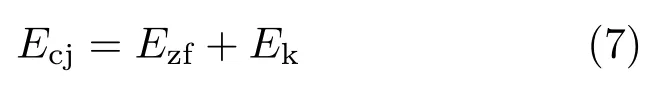
即

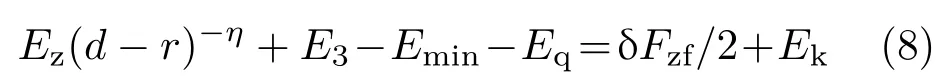
为防止巷道发生冲击地压，需要以煤岩动能形式向巷道释放的能量Ek等于零。如Ek大于零，即

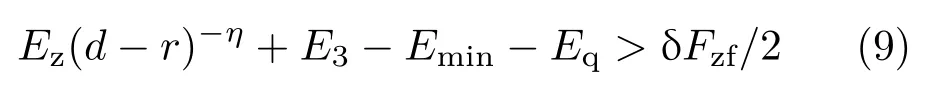
说明巷道支护结构不能完全吸收冲击地压释放能量，剩余能量Ek就会以煤岩动能形式向巷道释放，造成支护结构破坏、围岩垮塌。因此，式(9)是巷道冲击破坏失稳能量准则。

调查发现，造成伤亡事故的冲击地压现场巷道高度大多在1.0 m 以下，冲击地压发生后如果巷道高度仍保持在2.0 m 以上时基本不会造成人员伤亡。所以在冲击地压发生时，为保证煤矿工人生命安全，需要确保支护结构收缩量不大于某个极限值。因此，要使巷道支护结构吸收能量多，只能增加支护强度，这将导致巷道支护成本增加。震源一般未知，震源传递到巷道的能量不确定，为降低巷道支护成本，就需要避免巷道围岩弹性变形量积聚。因此，研究巷道围岩弹性变形积聚能量特征对降低巷道支护成本具有重要科学意义和应用价值。

2 矩形巷道围岩能量积聚计算模型

假设E为单位长度矩形巷道围岩积聚的弹性能，J；V岩为单位长度矩形巷道围岩中积聚弹性能的岩层体积，m3；ρ岩为岩层的能量密度，J/m3；V煤为单位长度矩形巷道围岩中积聚弹性能的煤层体积，m3；ρ煤为煤层的能量密度，J/m3。则单位长度矩形巷道围岩积聚弹性能为

矩形巷道围岩情况复杂，但以下三种类型具有一定代表性。第一种类型：煤层厚度等于巷道高度，如图1(a)。第二种类型：煤层厚度大于巷道围岩影响范围高度，如图1(b)。第三种类型：煤层厚度大于巷道高度，但小于巷道围岩影响范围高度，如图1(c)。论文以这三种类型为例，分析采深、巷道断面尺寸和煤层厚度等因素对矩形巷道围岩能量积聚影响规律。假定图1 中a为矩形巷道断面长度，m；b为矩形巷道断面高度，m；L为矩形巷道顶底板受影响范围，m；D为矩形巷道左右帮受影响范围，m；h为煤层厚度。

(1)第一种类型

单位长度矩形巷道围岩中积聚弹性能的岩层体积为

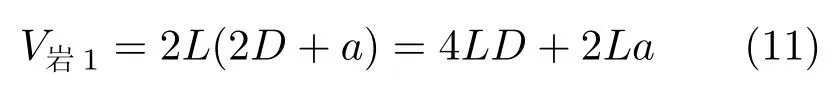
单位长度矩形巷道围岩中积聚弹性能的煤层体积为

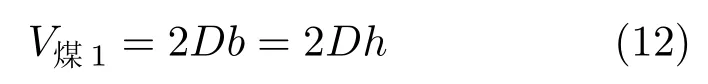
单位长度矩形巷道围岩积聚的弹性能为

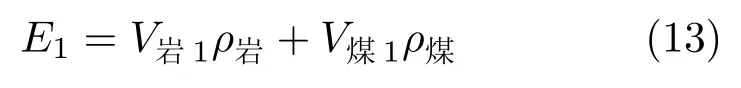
(2)第二种类型

单位长度矩形巷道围岩中积聚弹性能的岩层体积为

单位长度矩形巷道围岩中积聚弹性能的煤层体积为

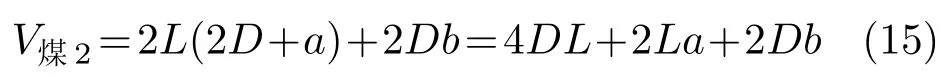
单位长度矩形巷道围岩积聚的弹性能为

(3)第三种类型

单位长度矩形巷道围岩中积聚弹性能的岩层体积为

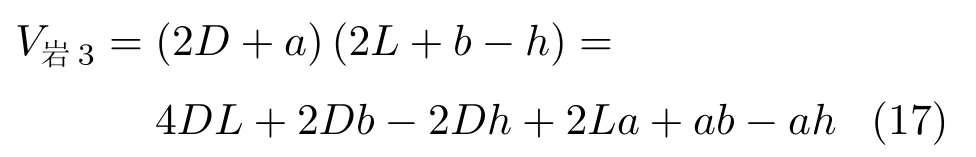
单位长度矩形巷道围岩中积聚弹性能的煤层体积为

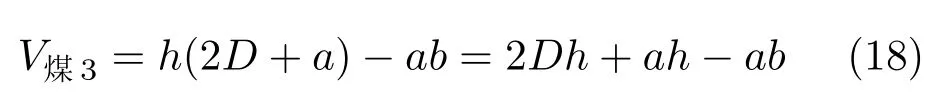
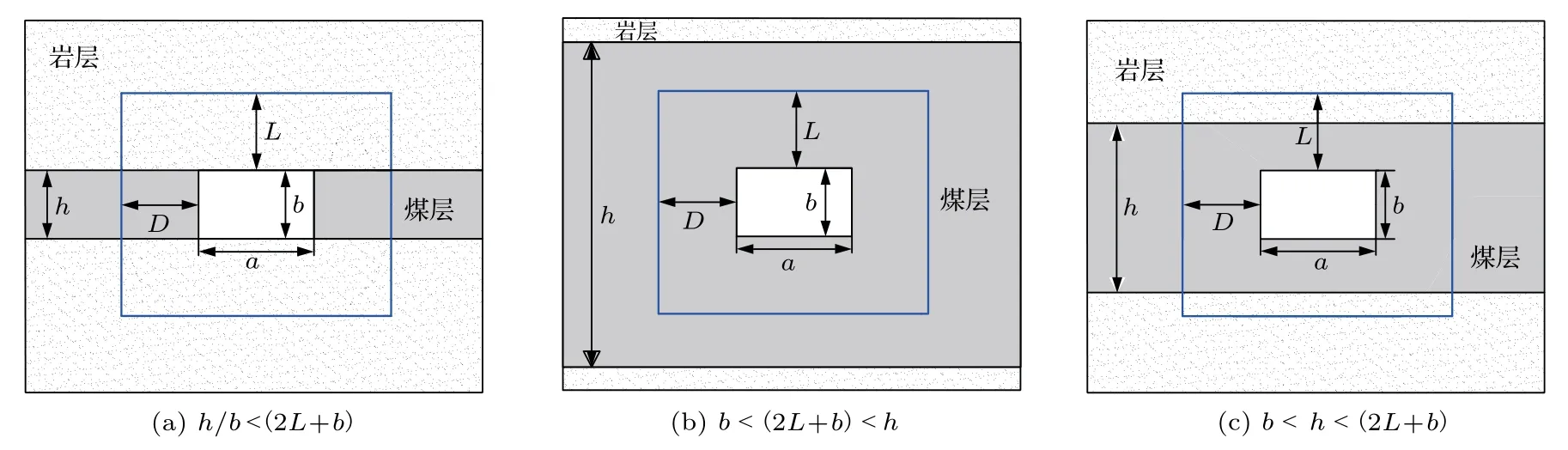
图1 矩形巷道围岩类型图

单位长度矩形巷道围岩积聚的弹性能为

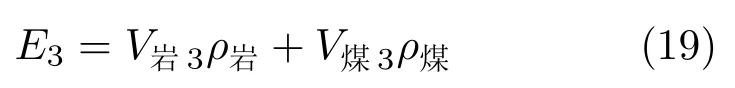
3 矩形巷道围岩能量积聚特征分析

地表以下埋深为H的煤岩层受到的自重应力[15-16]为

式中，σ为自重应力，Pa；γ为岩体容重，N/m3；H为上覆岩层厚度，m。

以平顶山十一矿矩形巷道为研究对象，取煤岩层容重为25.00 kN/m3。通过对煤岩样进行力学性质测试，计算出不同埋深条件下煤层与岩层的能量密度及自重应力，如表1。

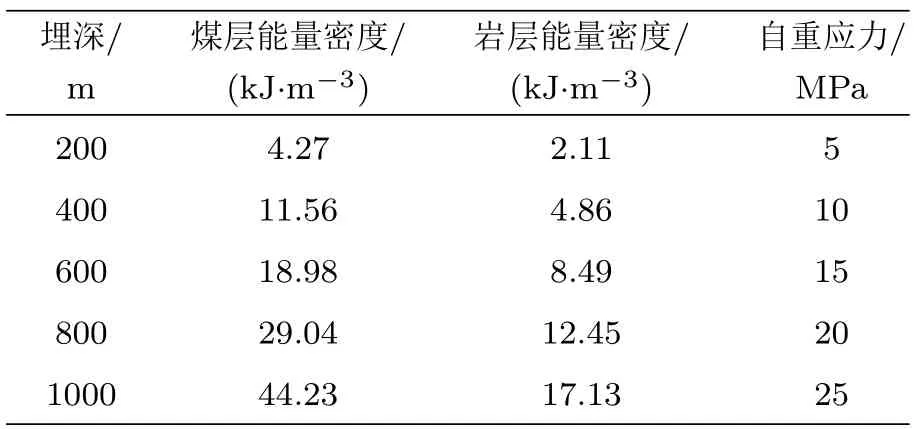
表1 不同埋深条件下煤层与岩层的能量密度

3.1 采深对巷道能量积聚影响规律

(1)采深对第一种类型巷道能量积聚影响规律

取巷道断面长度a= 5.00 m，高度b= 4.00 m，左右帮受影响范围D=5.00 m，顶底板受影响范围L= 4.00 m，煤层厚度h= 4.00 m，将参数代入式(13)，可得

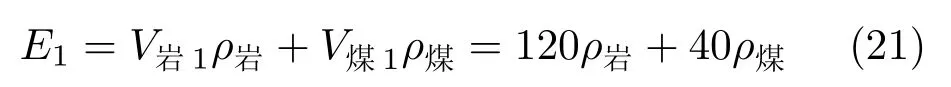
(2)采深对第二种类型巷道能量积聚影响规律

取巷道断面长度a= 5.00 m，高度b= 4.00 m，左右帮受影响范围D=5.00 m，顶底板受影响范围L= 4.00 m，煤层厚度h= 15.00 m (巷道在煤层中部)，将参数代入式(16)，可得

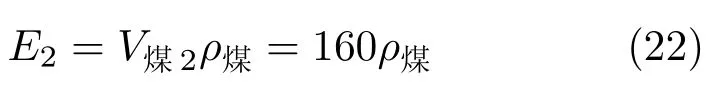
(3)采深对第三种类型巷道能量积聚影响规律

取巷道断面长度a= 5.00 m，高度b= 4.00 m，左右帮受影响范围D=5.00 m，顶底板受影响范围L= 4.00 m，煤层厚度h= 5.00 m (巷道在煤层中部)，将参数代入式(19)，可得

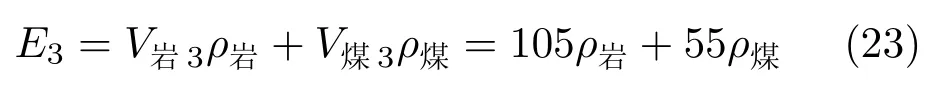
将不同埋深的煤岩能量密度分别代入式(21)，式(22)和式(23)，可得三种类型围岩巷道在不同埋深下单位长度矩形巷道围岩积聚的弹性能，如表2。采深对三种类型单位长度巷道能量积聚影响规律如图2。

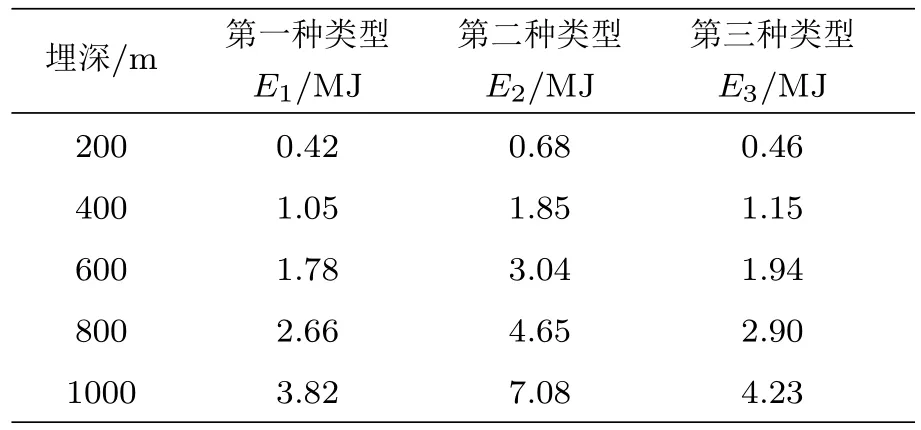
表2 不同埋深下单位长度巷道围岩积聚的弹性能

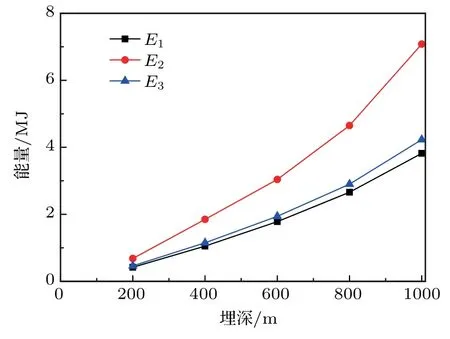
图2 采深对单位长度巷道能量积聚影响规律

从表2和图2可得：

(1)埋深为200 m，400 m，600 m，800 m，1000 m时，第一种类型单位长度积聚的弹性能分别为0.42 MJ，1.05 MJ，1.78 MJ，2.66 MJ，3.82 MJ；第二种类型单位长度积聚的弹性能分别为0.68 MJ，1.85 MJ，3.04 MJ，4.65 MJ，7.08 MJ；第三种类型单位长度积聚的弹性能分别为0.46 MJ，1.15 MJ，1.94 MJ，2.90 MJ，4.23 MJ。

(2)采深小于600 m时，三种类型矩形巷道单位长度积聚的弹性能均随采深的增加而线性增加；采深大于600 m 时，三种类型矩形巷道单位长度积聚的弹性能均随采深的增加而非线性增加。E2的增长速率最大，E1的增长速率最小。

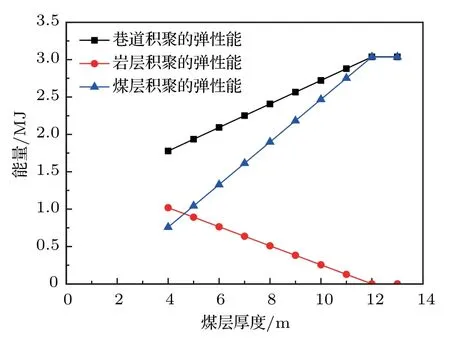
(3)相同采深时，三种类型矩形巷道单位长度积聚的弹性能E1

3.2 断面尺寸对巷道能量积聚影响规律

假定巷道埋深600 m，即ρ煤= 18.98 kJ/m3，ρ岩=8.49 kJ/m3。顶、底板受影响范围L均等于巷道断面高度b，左、右两帮受影响范围D均等于巷道断面高度长度a。以第二种类型为例，煤层厚度h= 15 m (巷道在煤层中部)，选取3 种不同巷道断面尺寸，分析断面尺寸对巷道能量积聚影响规律。3种巷道断面尺寸分别为：a=3 m，b=2 m；a=4 m，b=3 m；a=5 m，b=4 m。将参数代入式(16)，可得3种断面尺寸下单位长度巷道积聚能量，如表3。

表3 不同断面尺寸下单位长度巷道积聚能量

从表3可以得出，巷道断面面积为6 m2，12 m2，20 m2时，单位长度巷道积聚能量分别为0.89 MJ，1.78 MJ，2.96 MJ。巷道尺寸大，围岩积聚能量也增大，但巷道尺寸小又不利于巷道维护。因此，在满足巷道使用条件下，可以减小巷道断面尺寸。

3.3 煤层厚度对巷道能量积聚影响规律

假定巷道埋深600 m，即ρ煤= 18.98 kJ/m3，ρ岩= 8.49 kJ/m3。巷道断面长度a= 5 m，高度b=4 m，顶、底板受影响范围L均等于巷道断面高度b，左、右两帮受影响范围D均等于巷道断面高度长度a。研究煤层厚度分别为4 m，5 m，6 m，7 m，8 m，9 m，10 m，11 m，12 m，13 m 时，巷道能量积聚规律(巷道在煤层中部)。根据不同情况，将参数代入式(13)或式(16)或式(19)，得出不同煤层厚度下单位长度巷道积聚能量，如表4。不同煤层厚度下单位长度巷道积聚能量、岩层积聚能量和煤层积聚能量如图3。