深度学习在飞行器动力学与控制中的应用研究综述

程 林 蒋方华 李俊峰

(清华大学航天航空学院，北京100084)

中国航空航天经过60余载的奋力发展，在几代双航人的努力拼搏下，通过打造长征、神州、嫦娥等系列工程，跻身于世界强国行列。然而，我国航空航天也面临着总体布局大而不强，部分技术与欧美强国存在巨大差距的现状。飞行器控制系统是航空航天飞行器调度各分系统的“大脑”，直接决定了整个飞行任务的形式和质量。提高飞行控制的自主性、鲁棒性和智能化水平是飞行器动力学与控制技术研究的主题。

传统上，受到机载计算机软硬件技术限制，飞行器控制系统难以实现飞行剖面的实时规划。工程上，多以离线标称轨迹设计和在线标称轨迹跟踪相结合的跟踪制导方式实现飞行任务。以经典控制理论为基础发展起来的PID(proportion-integralderivative)控制技术和以极点配置、滑模控制[1]、自适应控制[2]、鲁棒控制为代表的现代反馈技术能够基于当前状态解析计算控制指令，具有算法简单易实现、实时性好、稳定可靠的优势，至今被绝大多数飞行任务所采用。然而，此类方法基于当前状态(非全局)生成指令，导致其对全局约束和性能指标的考量不足。当飞行任务包含复杂约束和最优指标时，飞行控制系统往往需要离线设计好的标称轨迹作为飞行参考，PID 技术和现代反馈控制技术用于标称的轨迹跟踪和姿态调整。由于标称轨迹离线设计所得，此类标称轨迹跟踪制导方式的自主性和鲁棒性较差，尤其是当飞行环境存在较大的不确定性时。随着任务需求的不断发展，未来飞行任务的控制复杂性也日益提高。例如，高超声速飞行器再入飞行轨迹实时规划的需求、末制导中多个终端约束的严格限制、以太阳帆为代表的欠驱动控制模式、小行星着陆任务中的远程通讯限制等都对未来飞行控制系统全局自主决策能力和智能化水平提出更高的要求。从技术的发展趋势来看，为满足未来强不确定性、欠驱动、多约束、通讯限制等任务特点，需要发展新型动力学与控制技术，以实现控制任务自主性、鲁棒性、多约束满足和实时智能决策等性能的全面提升。

近年来，人工智能技术的飞速发展为飞行器自主智能飞行的实现提供了新的可能[3]。人工智能是计算机科学的一个分支领域，主要研究人类智能活动的规律，构造具有一定智能的人工系统，也就是研究如何应用计算机的软硬件来模拟人类某些智能行为的基本理论、方法和技术[4]。人工智能属于应用范畴，在算法层面主要依赖机器学习算法。机器学习又可分为监督学习、非监督学习和强化学习[4]。其中，深度神经网络飞跃式发展促进了近年来机器学习研究的再次活跃，引领了第三次人工智能的浪潮。深度神经网络映射能力好、学习能力强、适应性广、纯数据驱动的优点使其在图像识别、自然语言处理、健康医疗等任务中具有超过人类的表现[5]。深度学习主要实现数据的函数映射功能，可用来解决智能中的辨识问题。不同的是，强化学习针对Markov决策问题，通过与被控对象的不断交互和迭代学习，生成可供全局决策的最优策略，可解决智能中的决策问题[6]。深度神经网络为强化学习的智能存储提供了强大记忆载体。应运而生的深度强化学习技术适合于解决复杂且难以建模的应用场景问题，其有效性在围棋AlphaZero算法中得到验证[7]。深度强化学习技术已经在工业自动化、数据科学、神经网络优化、医学等方面逐渐开展应用[8]。总而言之，人工智能基于存储、记忆、预训练的应用模式为传统学科难题的解决提供了新途径。近年来，人工智能技术应用于飞行器动力学与控制，用以提升飞行控制的自主性和智能化水平，尤其备受关注。

本文基于课题组前期研究成果和参阅国内外知名学者的部分研究，以提升飞行器控制自主性和智能化水平为研究主题，总结和梳理了深度学习应用于动力学、最优控制和任务设计中的研究思路，并针对研究思路的总体实现方案、优缺点和部分代表性成果进行综述，希望对相关研究同行提供一定的参考。深度学习应用于航空航天的研究方兴未艾，新的成果更是层出不穷，论文未能提及之处，敬请谅解。

1 深度学习在动力学中的应用

为提高飞行器自主飞行控制质量，可以从以下两方面入手。第一，提高飞行在线智能决策能力；第二，建立更加精确的飞行器动力学模型。精确的动力学模型是实现飞行器运动规律推演的基础，也是控制器智能决策的重要依据。传统动力学以牛顿力学和分析力学为基础，结合一定力学经验和工程要求，建立飞行器飞行动力学模型。然而，受到模型不匹配、测量手段不足、精确建模成本过高、模型迁移等诸多因素影响，实际工程中难以获得飞行器精确动力学模型。例如，小行星着陆过程中，小行星参数不确定会导致引力场计算模型的不准确；基于理论分析和风洞试验获取的临近空间飞行器气动模型也存在较大不准确，以及风干扰因素也难以建模；软体机器人目前还没有系统的动力学建模方法等。飞行器动力学模型的一般形式为

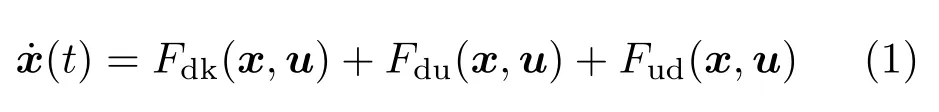
其中，模型分为确定性部分(deterministic)和不确定性(undeterministic)部分。确定性部分表示在相同的状态下具有确定的动力学特性，具有可复现性，例如推力或者重力等影响因素。不确定性部分表示在相同状态下动力学呈现不确定特征，例如飞行器的风干扰等。表达式Fdk(x,u)表示动力学模型中确定且已知(known)部分，Fdu(x,u)表示动力学模型中确定但未知(unknown)部分，Fud(x,u)则表示不确定性部分。

目前深度学习在动力学建模的应用主要包括：(1)提升计算效率；(2)构造智能动力学模型；(3)动力学反问题的学习。

1.1 提升计算效率

在某些控制问题中，动力学部分Fdk(x,u)尽管已知，但是计算量庞大。在这种情况下，机器学习算法可用于拟合动力学Fdk(x,u) 部分，在保证精度的前提下实现计算效率的提升。例如，Furfaro等[9]采用极限学习机(extreme learning machines)学习不规则小行星的引力场，在确保一定拟合精度的同时大幅提高了引力场计算效率。Song 等[10]采用深度神经网络拟合不规则引力场，并将其应用于小行星着陆轨迹规划中，取得了良好的效果。Cheng等[11-12]进一步将神经网络引力场模型应用于小行星着陆轨迹的快速同伦和智能着陆控制器学习中。此外，Wei等[13]采用Serendipity(偶然)插值技术来拟合小行星引力场的起伏，从而获得高计算效率、高精度的小行星引力场模型。

1.2 构造智能动力学模型

为了进一步提升飞行器动力学建模的精度，深度神经网络也可用来学习动力学的未知部分Fdu(x,u)。文献[3]中提出一种智能动力学模型

其中，深度神经网络模块Netdu(x)用来表征动力学中的Fdu(x,u)部分，ϵf表示拟合误差。为了实现模型的自我学习，文献[3] 基于扩张观测技术提出了一种模型迭代学习算法，并给出了详细的算法稳定性证明。值得说明的是，文献[3]为了保证后续间接法的求解需要，只考虑动力学Fdu(x,u)与控制变量u无关的情况。式(2)也被尝试应用于小行星绕飞过程中的引力场在线学习。小行星探测器前期绕飞中，通过一定的反演算法，推算出当前位置下的引力场修正值。观测的引力场修正值与地面雷达或者光学估算值(例如多面体算法[14])进行数据融合，从而实现智能动力学模型的在线调整与学习。基于引力场的学习效果，研究者还可以进一步对探测器绕飞轨道进行优化。当前，针对反演算法、数据融合算法、绕飞轨道的优化还在技术攻关中。

与此同时，相关学者也在设想更加一般性的智能动力学模型。例如，考虑Fdu(x,u)与控制变量u相关，且也可应用于间接法的动力学模型

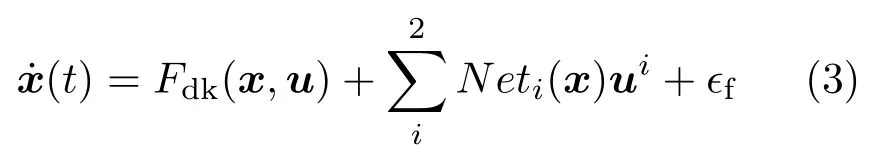
其中，i=0,1,2；Fdu(x,u)的拟合为一元三次表达式，三个网络Neti(x)分别表征一元三次表达式的三个拟合系数。考虑到动力学中可能存在不确定项，也可考虑含正态分布随机项的动力学模型

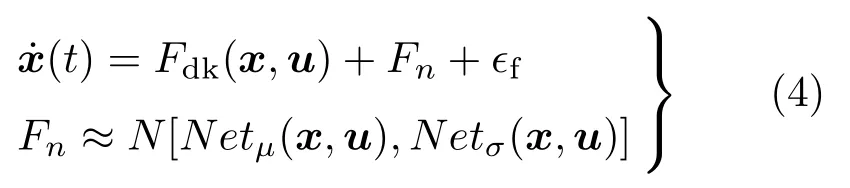
其中，函数N(µ,σ)表示正态分布函数，µ=Netµ(x,u) 表示正态分布的期望，σ=Netσ(x,u)表示正态分布的方差。

作者认为，精确动力学建模是实现飞行器智能飞行不可缺少的关键技术之一。目前，计算机领域崇尚Model-free 的学习策略，即在不需要对被控对象精确建模的前提下，通过智能体与被控对象的不断交互和经验积累，最终实现智能体最佳控制策略的学习。近年来，深度强化学习领域出现的代表性算法也多为Model-free算法，例如DDPG (deterministic policy gradient algorithms)[15]，A3C (actorcritic)[8]，区域信赖策略优化(trust region policy optimization, TRPO)[16]，PPO (proximal policy optimization)[17]等。尽管Model-free的学习策略在实践中简单易执行且具有良好的收敛性，但是Modelfree 强化学习算法也存在明显的缺点，包括随机动作探索引发的学习效率低下、约束无法严格保障、以及训练样本的海量需求。在不解决以上难题的情况下，作者认为Model-free 强化学习算法难以直接应用于飞行控制器的设计任务中。

另一方面，基于模型的策略学习在飞行控制任务中具有以下优势。第一，基于牛顿力学或分析力学可获取动力学模型的基本形式和解析表达式，这些先验信息的充分利用可有效降低问题的复杂性和学习样本的需求量。例如，速度和位置的关系是明确的、解析的。第二，精确构建被控对象的动力学模型，可有效降低智能控制器与实物的交互需求，从而降低学习成本。当然，被控对象动力学模型越准确，与实物交互的需求降低效果越明显。这也间接说明了打造具有自学习能力的智能动力学模型的必要性。在最新ANYmal 四足复杂机器人智能控制系统构造中，数字动力学模型就被用于训练控制策略，并取得非常好的实际控制效果[18]。近五年，Model-based 深度强化学习的研究也备受学者关注，其中构建精确的表征模型也是其关键技术之一[13,19]。文献[20]基于高斯处理技术打造贝叶斯神经网络模型(Bayesian neural network dynamics model)跟本文式(4)具有相同的研究思路。区别在于，式(4)包含传统动力学模块Fdk(x,u)，是一种复合模型，具有继承动力学理论分析结果的优势。

1.3 动力学反问题的学习

飞行器控制的主要目的是根据任务需求调整控制指令实现预定的控制规律。从具体实现途径来看，主要有反馈控制(基于李雅普诺夫稳定性定理)、最优控制(基于极小值原理)和深度强化学习(基于贝尔曼最优性原理)三种实现途径。其中基于当前状态解析生成控制指令的反馈控制具有易于实现、实时性好、稳定可靠的优点。反馈控制又可细分为Error-based 方法(误差反馈方法，包括PID 和增益调度PID等)和Model-based方法(模型反馈方法，包括动态逆、滑模、自适应控制等)[21]。Error-based方法不依赖被控对象的精确模型，方法简单易于实现，是目前工程中应用最为广泛的控制手段。与此同时，基于现代控制理论发展起来的Model-based控制方法能够根据被控对象动力学特点，精确控制被控对象状态的微分变化过程，从而能够充分发挥被动对象的动力学特性，实现更快、更稳的控制效果。图1 给出了Model-based 反馈控制方法的示意图。Model-based 反馈控制的实现可分为两个操作：第一，算法根据反馈回来的状态和想要的控制目标设计出想要的状态微分变化，其中状态微分变化的不同设计策略也是动态逆、滑模等方法的主要区别；第二，算法根据微分动力学模型和想要的状态微分变化值反向计算需要的控制指令。然而，由于实际飞行控制中被控对象的动力学模型难以精确获得，这极大限制了Model-based 方法在工程中的应用。为了解决此类问题，Model-based 方法主要朝着两个方向改进，一个是提高算法的自适应性，即通过在线观测理想模型和实际模型的偏差∆F，并在反馈控制中实时补偿；二是提高算法的鲁棒性。

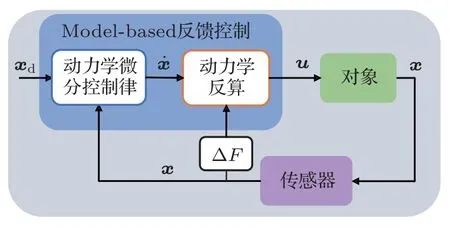
图1 Model-based 方法示意图

Model-based 反馈控制方法依赖精确动力学模型反向计算控制指令，而工程上又难以实现。深度学习有望解决这一难题。图2给出了一套解决方案。方案主要包括三部分。第一，采用扩张观测器对未知状态和状态微分在线辨识，获取精确状态是对状态进行精确控制的前提；第二，基于极点配置方法配置稳定可控的状态微分变化规律，此部分主要继承于传统Model-based 方法；第三，神经网络根据状态微分变化规律预测具体的控制指令。考虑到在没有任何先验信息的情况下，神经网络一开始的输出是随机的、错误的，因此可加入一个PI反馈控制器进行神经网络的引导学习。具体过程为：被控对象的指令u由神经网络的预测指令unet和PI 控制器的∆u复合而成。初始，由于神经网络的输出不准确，被控对象的实际状态微分˙x和理想状态微分˙xd存在差距。在这种情况下，PI控制器会根据差距产生补偿指令∆u，缩小神经网络指令unet的误差。与此同时，神经网络会根据补偿指令∆u的大小对自身参数进行调整，使其输出unet尽可能趋向于修正后的u。当算法稳定后，unet→u，∆u →0。在这种情况下，尽管Fdu(x,u)不知，状态微分以及unet→L−1(Fdk(x,u)+Fdu(x,u)) (L−1表示反求u，即动力学问题的逆)。详细的方法设计和稳定性证明会在后续的文章中给出。

图2 智能控制器示意图

2 深度学习在最优控制中的应用

飞行控制的技术实现途径主要包括反馈控制、最优控制和强化学习。反馈控制基于当前状态解析计算控制指令，具有良好的实时性和算法收敛性，但是算法没有全局规划能力，对过程约束、终端约束和优化指标难以考量。飞行控制问题本质是最优控制问题，常见的最优控制数值求解方法包括间接法和直接法[22]。间接法利用Pontryagin 极小值原理推导出最优控制的一阶必要条件，进而得到求解最优轨迹的两边边值问题[23]。从优点来看，间接法求解的结果精度比较高，且解满足一阶最优性。但是，在实际中，两边边值问题求解难度比较大，尤其是当控制量和状态量均存在约束时。除此之外，它还具有推导过程繁琐、通用性差、初始值难以估计、收敛域小等缺点。近年来，包括同伦技术[24]、协态归一[25]、启发式初始值搜索[25]等策略用来改进间接法的性能，并取得良好的效果。得益于计算机性能的提升和数值仿真技术发展，自20 世纪70 年代以来，最优控制数值求解的另一重要分支——直接法得到兴起并被普遍采用[26]。直接法采用剖面参数化的方法将最优控制问题转化为参数优化问题，并采用非线性规划方法进行求解。根据对控制量和状态量是否参数化，直接法又可细分为只离散控制剖面的直接打靶法、同时离散控制剖面和状态剖面的配点法，以及只离散状态剖面的微分包含法[27]。直接打靶法是轨迹设计中常用的一种形式，大量方法(包括依赖梯度的最优化算法和随机启发式算法)都曾结合直接打靶法用来解决最优控制问题[28]。然而，由于直接打靶法中状态剖面只能靠弹道积分得到，整个算法的实时性比较差。近年来，以伪谱法[29-30]和凸优化[31-33]为代表的配点法凭借收敛速度和可靠性等优势而备受学者关注。然而，配点法面临维度爆炸、收敛域小、求解时间和精度严重依赖于初始猜测值等难题。总而言之，最优控制数值求解方法是目前最优控制问题的主流求解方法，求解稳定性和速度上也在逐年完善。然而，由于仍然不能满足飞行器在线控制的实时性要求，最优控制数值求解方法目前主要应用于离线的标称轨迹设计以及在线的标称轨迹紧急重构。

强化学习作为当今人工智能研究的一个重要研究方向，在解决连续动作空间的最优控制问题上优势不断凸显，并在机器人控制、自动驾驶等方面展现出很好的应用前景[34]。强化学习算法是机器学习算法的三大分支之一，它主要研究在交互环境下，智能体根据当前状态不断尝试动作并总结得失，最终实现累计效益最大化的控制策略(如图3所示)。

图3 强化学习交互过程

强化学习基于动态规划方法的贝尔曼最优性原理，它与传统最优控制数值求解方法(间接法和直接法)的区别主要体现在：

(1) 最优控制数值求解方法：前期不需要训练，每次求解都试图得到整个动作序列(离散问题)或者控制剖面(连续动作问题)，由于求解维度很大，求解实时性普遍不足；

(2) 强化学习方法：强化学习基于最优性原理将多级决策问题转化为一系列单级决策问题，具体公式为：当前状态的好坏=当前动作的奖励＋下一个状态的好坏[6]。强化学习以离线反复学习为代价，根据状态和动作对应的价值函数来优化动作指令，经过反复训练得到最优控制策略；在在线应用阶段，训练得到的最优控制策略无需求解最优控制问题，能够根据状态查询得到最优指令，因此具有显著的实时性优势。

深度强化学习是采用深度神经网络做函数拟合的一类新兴强化学习算法，特别适合解决复杂大维度应用场景问题，并已经在围棋AlphaZero 算法中得到技术验证[7]。在连续动作空间最优控制问题上，2014年，Deepmind团队在总结DQN[35]和Actor-Critic 方法基础上，提出了DDPG 方法[15]，实验表明，DDPG 算法在连续动作空间任务中表现稳定，且计算量远远低于同水平DQN。Schulman等[16]于2015 年提出了TRPO方法，此方法通过强制限制同一批次数据新旧两种策略预测分布的KL差距，避免参数更新中策略发生太大改变，从而提高了算法的收敛性能。2016年，Deepmind团队提出了A3C异步强化学习架构，其在采用深度强化学习Actor-Critic 框架基础上，利用多个智能体共同探索，并行计算策略梯度，维持一个总的更新量[8]。针对TRPO 标准解法计算量过大的问题，OpenAI 于2016 年提出了利用一阶梯度的PPO算法，并用随机梯度下降的方法更新参数[17]。Google 在此启发下，基于PPO 算法提出了分布式的DPPO (distributed proximal policy optimization)，并取得了优异的结果[36]。鉴于PPO 算法依旧沿着策略梯度方向进行参数更新，2017 年8 月，多伦多大学和纽约大学联合提出ACKTR 算法，其通过引入计算参数的自然策略梯度来加速PPO算法的收敛速度[37]。

强化学习起源于离散多级最优决策问题，将其推广到连续飞行控制问题中，现有强化学习算法主要面临着以下三个挑战：(1)策略学习效率问题：现有强化学习动作选择大多采用随机探索策略，虽然一定程度上保证了算法的探索能力，但是同样导致算法计算效率低下和复杂问题难以收敛等不足。(2)收益函数设计：现有强化学习的价值函数难以考量约束满足情况，单纯以惩罚函数的形式来评价策略的实现情况，很容易导致问题的病态，此难题导致强化学习难以在约束较强的最优控制问题上应用；(3)学习成本问题:无模型依赖引发海量样本训练需求。

从目前技术途径来看，无论是最优控制数值方法还是深度强化学习在飞行器实时自主控制中都存在着不足。作者认为传统学科与新兴人工智能的关系并非取代关系，而应该相辅相成。实现传统飞行控制与人工智能技术的创新性结合，是实现智能控制发展的重要方向。目前深度学习与传统控制方法相结合的研究可概括为以下三个方面：(1)深度学习拟合控制指令；(2)智能初值生成策略；(3)交互强化学习。

2.1 深度学习拟合控制指令

虽然最优控制数值求解方法在在线飞行控制中实时性不足，但是其求解效率高、算法收敛性好。在动力学模型已知的情况下，可以通过收集最优控制数值方法生成的飞行控制样本，离线训练深度神经网络，并应用于在线飞行控制中。这是人工智能应用于飞行控制中最为直接的方案之一。针对着陆控制问题，Sanchez-Sanchez 等[38-39]基于间接法生成的求解数据，采用监督学习的方式训练深度神经网络，仿真表明，训练得到的智能控制器能够实时驱动被控对象完成比较精确的着陆。在月球着陆控制任务中，Furfaro 等[40]采用GPOPS 产生训练数据训练卷积神经网络(convolutional neural networks,CNN) 和循环神经网络(recurrent neural networks,RNN)，训练得到的智能控制器能够基于图像数据自主决策控制指令。文献[41-44]将类似方案应用于小行星着陆、火星着陆以及小推力多圈轨迹转移、四旋翼无人机机动中，都取得不错的仿真效果。Izzo等[45]讨论了深度学习对控制指令、价值函数、协态(价值函数梯度)的三种拟合策略，并得出对控制指令和协态进行拟合的策略表现更好的结论。在文献[46] 中，训练好的神经网络被用来实时决策飞行器姿态脉冲发动机的开关，验证了此方案在离散控制决策问题上的可能性。

为实现智能控制器任意状态的拟合，神经网络的训练往往需要大量数据支持。如何快速产生大量数据需要一定的技巧。在间接法生成训练数据中，文献[39]采用如下策略：首先，在上一个状态周围随机产生下一个样本状态；然后，以上一个状态的协态值作为下一个状态协态求解的初始猜测。周而复始逐步生成样本集。在此基础上，文献[47]采用了一种遍历状态空间的样本生成策略，在保证样本快速生成的前提下，确保了样本集对搜索空间的覆盖性。同样，同伦技术也可用来提升样本的生成效率[41]。Izzo 等[45]基于极小值原理，提出了基于反向积分快速获取样本的思路。虽然该套方法在样本覆盖性、搜索空间边界上还需要进一步开展研究，但是通过单次轨迹反向积分即可获取最优轨迹的策略在算法效率上表现出无与伦比的优势。

神经网络应用于飞行控制中最受诟病的一点是，神经网络是一个黑盒子，其控制效果难以解析分析。为了提升智能控制器的可靠性，文献[48]在太阳帆轨迹转移中，采用多个尺度的神经网络相互配合，从而保证神经网络能够识别10−7量级的状态误差，最终实现飞行器高精度入轨。在月球着陆任务中，文献[49]提出智能控制和反馈控制复合的控制策略，从而保证飞行器在大范围机动中呈现最优性而在最后着陆阶段又兼具高可靠性。

总体来看，最优控制数值方法产生训练样本，深度学习离线训练智能控制器并应用于在线控制的方案，既利用了最优控制方法在求解质量和效率上的优势，又解决了传统最优控制方法在线控制中实时性不足的难题。然而，该套方案依赖精确动力学建模，这极大限制了这一方案的通用性。动力学建模的不准确或者动力学的迁移都将导致训练好的控制器作废。为了解决此问题，该方案可以结合本文动力学部分中的智能动力学模型进行复合应用。

2.2 智能初值生成策略

在以上深度学习拟合控制指令的策略中，传统最优控制方法产生训练样本，神经网络学习样本并被应用于在线控制。整个策略中，最优控制方法是“辅助”角色，而人工智能算法是“主要”角色。然而，当动力学模型存在不确定时，深度学习拟合控制指令的策略会失效。针对此问题，更加保守但可靠的思路是人工智能算法退居“辅助”角色。一种切实可行的方案是离线训练好的神经网络为最优控制数值方法提供求解初值，促进其求解效率和速度。在离线状态下，当动力学模型(1)中存在未知项时，可以基于动力学模型

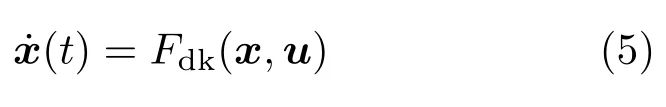
产生样本并训练网络。在线状态下，且未知动力学项已经探明后，原问题(1)的解可由问题(5)的解延拓得到。文献[47]针对小行星着陆问题给出了一套解决方案。在此论文中，通过模型简化和线性转换，小行星着陆问题可被简化为一个二维空间转移问题。间接法离线求解二维空间转移问题，产生的控制样本用来训练神经网络。仿真表明，神经网络可为二维转移问题提供100%收敛的初始解。在此基础上，原小行星着陆问题可基于反向模型延拓技术而快速求解。此外，论文还设计了初值生成备用策略，进一步提升求解的可靠性。

由于未知动力学部分可以在神经网络离线训练中临时舍弃，等动力学探明之后再补充进来，所以算法的适应性比较好。例如文献[47]，由于忽略了小行星的自转和引力场，因此训练好的神经网络适用于在任何小行星任意地点的着陆任务。与此同时，由于神经网络只是为最优控制方法提供初值，单纯起辅助作用，因此整套方案的可靠性也有所保障，这一点在工程中尤为重视。

2.3 交互强化学习

Model-free 强化学习算法不依赖被控对象的数学模型，智能体通过不断与被控对象的交互，总结动作的收益情况最终形成最优控制策略。Model-free强化学习算法在通用性和易用性上具有诱人的应用前景。然而，正如前文提到，Model-free 强化学习算法在飞行控制中应用，存在收敛效率、约束管理和学习成本三个难题。在不解决以上难题的情况下，作者认为Model-free 强化学习算法难以直接应用于飞行控制器的设计任务中。要想降低飞行控制中强化学习算法的学习成本，一种可行的方案是构建被控对象的数学模型(model)，通过Model-free强化学习算法与数学模型的交互完成智能控制器的训练。例如，文献[50] 将Model-free 强化学习算法应用于火星着陆任务中。仿真试验表明，学习的智能控制器能够在六自由度控制中自主决策控制指令，并具有一定的控制鲁棒性。然而，终端等式约束和飞行最优性指标是以罚函数的形式添加到强化学习的Reward 函数设计中，导致训练好的控制器只能实现约束和最优性的折衷。在已知动力学模型情况下，Model-based强化学习的研究也备受关注[19]。

鉴于最优控制数值方法相比Model-free 强化学习算法在求解效率和约束满足情况都有显著的优势，文献[48]提出一种Actor–Indirect method 交互式策略学习架构。在此架构中，间接法(indirect method)求解飞行控制问题，提供样本训练神经网络Actor(神经网络既学习控制指令又学习协态)，而神经网络Actor 反过来为间接法提供良好的协态初值从而促进间接法的打靶效率。在交互式策略学习架构中，随着学习的深入，神经网络Actor 辅助间接法求解的作用不断强化。仿真表明，在太阳帆轨迹转移、小行星着陆任务中，神经网络Actor 后期可为间接法提供收敛率接近100%的良好初值。虽然此交互式学习策略能不能算作Model-based 强化学习算法尚待学术界商榷，但是最优控制数值方法和神经网络之间的相互强化作用却是明确的。

为了进一步解决动力学模型中可能存在的未知部分，文献[3]进一步构建智能动力学Identifier 模块。借助于算法与实物的交互，不断提升数字模型的准确性。从而在减少与实物交互的情况下尽可能提升策略的学习效果。文献[3]最终提出新型Identifier–Actor–Optimizer 交互式策略学习架构，如图4所示。新型架构在模型依赖、算法学习效率、应用灵活性上都具有一定优势。

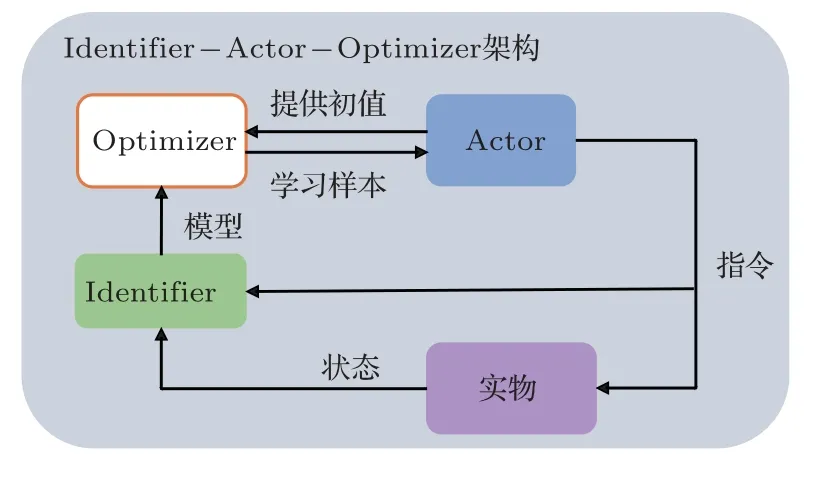
图4 Identifier–Actor–Optimizer 架构

3 深度学习在任务设计中的应用

人工智能算法在飞行任务设计方面同样具有出色的应用前景。传统上，需要对整个飞行问题进行确定性的求解，才能评估任务执行的总体性能。虽然预估精度可以保证，但是整个过程往往耗时耗力。机器学习基于历史经验数据，能够近似拟合状态和总体性能之间的非线性函数关系。基于机器学习算法的总体性能快速预估对于整个任务优化效率的提升具有显著效果。机器学习算法尤其适用于对飞行性能预估精度有一定容忍、但是对预估快速性具有较高要求的任务设计场景。由于飞行任务优化问题的各式各样，深度学习在任务设计中的具体应用形式也呈现多样性。文献[51-53]运用深度神经网络拟合小推力轨迹转移中的质量消耗，实现了良好精度的燃料消耗快速预估。Song 等[54]利用深度神经网络拟合太阳帆转移中的最小时间，为太阳帆的小行星探测序列快速规划提供依据。在文献[55]中，深度学习被用来支持飞机防碰撞预警系统的决策。基于历史观测数据，深度学习可用来提升卫星轨道的预测精度[56]。此外，深度学习还被用于小推力探测器轨道转移可达性的预测任务中[53]。深度学习在飞行器射程的预测、小行星轨道的稳定性分析、卫星可达域的预测、卫星的碎片预警等任务中也呈现出色的应用潜力。

4 总结与展望

深度学习是目前人工智能领域最受关注的研究方向之一，也是飞行器智能飞行控制系统中最有可能用到的机器学习算法之一。深度学习用以解决飞行器飞行动力学与控制难题具有显著的学术和应用前景，同时也衍生出一系列需要进一步解决的难题。基于前期研究经历，在此分享四点建议。

(1) 经典动力学与控制技术、新兴人工智能技术各自具有优势和不足，他们之间不应是取代关系，而应是通过双方的交叉融合实现优势的互补。经典动力学与控制技术发展到今天，存在一定的技术瓶颈。百尺竿头更进一步，动力学与控制技术应当充分认识和吸收人工智能的优势，尤其是深度学习的存储、记忆、预训练的应用模式。与此同时，围绕飞行控制设计任务，纯人工智能算法忽视被控对象自身动力学和控制规律、信奉纯数据驱动的“懒汉”策略也注定是低效的、无用的。围绕经典动力学、控制技术与新兴人工智能技术创新性结合的研究将是飞行器智能控制领域重要研究方向。

(2) 深度学习为传统学科难题的解决提供新的工具，但它也仅仅是工具而已。从应用上看，深度学习为传统学科提供了存储、记忆、预训练的新应用模式，解决了传统技术目前遇到的一些难题，尤其是实时性难题。然而从数学上来看，神经网络也仅仅是承担了数据间的函数拟合功能。在飞行智能控制器的设计中，人工智能算法的实现往往并非最大的技术瓶颈，而真正的关键技术往往在于，如何通过一系列建模和简化手段，将原飞行控制问题转换成一个人工智能算法可以解决和善于解决的问题。实践表明，转换后的问题越明确、越简单，就越有助于智能策略学习效率和收敛性的提升。

(3) 人工智能当前仍处于计算智能阶段，训练好的神经网络只是在训练集范围内具有可靠的表现，目前无范围外的推演能力。考虑到飞行控制问题大多是非线性控制问题，因此训练好的神经网络在数据集范围外的效果并不能保证。如何构建问题及确定训练集的边界，保证训练数据的覆盖性也是未来研究的重要议题。

(4) 智能动力学模型是未来智能飞行控制实现的关键之一。目前人工智能与飞行控制的结合更多关注的是控制本身，而对动力学部分关注比较少。以Model-free 强化学习为代表的方法甚至试图直接忽略被控对象的动力学特征，单纯靠数据驱动来实现最优控制策略的学习。不可否认，此类方法在某些特殊问题上是适用的，例如没有交互成本的虚拟游戏、难以动力学建模的互联网交互活动。但是在飞行控制中，考虑到学习效率和交互成本，动力学模型依然无可替代。与此同时，比起不同控制器不同参数对控制规律的影响的复杂性，动力学模型是推演未来飞行规律的基础，更加易于人工智能算法学习的实现。

本文以提升飞行器飞行控制自主性和智能化水平为研究主题，在总结动力学与控制技术当前存在难题的基础上，梳理了深度学习应用在飞行器动力学、控制和任务设计的研究思路，并针对研究思路的总体实现方案、优缺点和部分代表性成果进行了综述。最后，论文给出了深度学习在飞行器动力学与控制中应用的四点建议。