一种双孔空心预制梁抗弯性能试验

2020-07-02马少春张政浩1b田重榜

河南科技大学学报(自然科学版) 2020年6期

马少春，张政浩，鲍鹏,1b，田重榜

(1.河南大学 a.土木建筑学院；b.开封市工程修复与材料循环工程技术研究中心，河南开封 475004;2.郑州大学水利科学与工程学院，河南郑州 450001)

0 引言

从20世纪80年代开始，中国针对轻混凝土结构的力学性能进行了试验，并取得了大量关于结构构件受弯和受剪等方面的研究成果。文献[1]通过完成对称集中荷载作用下，不同截面高度和不同剪跨比的15根高强轻骨料混凝土受弯构件力学性能试验，揭示了尺寸效应对受弯构件的作用机理。文献[2]通过对16根钢筋轻混凝土无腹筋梁进行试验，提出了无腹筋轻骨料混凝土梁的受剪承载力计算建议公式。文献[3]以陶粒及废砖作为再生混凝土梁的主要填充骨料，提出了该梁的受弯承载力计算公式。文献[4]针对HRB500高强钢筋页岩陶粒轻骨料混凝土叠合梁进行了受力试验，修正了短期最大裂缝宽度计算公式，并得出该种梁斜截面受剪承载力比传统封闭箍筋梁低的结果。文献[5]进行了高强钢筋陶粒混凝土梁受弯试验，对JGJ 12—2006《轻骨料混凝土结构技术规程》中裂缝计算公式的适用性进行了评估，并提出了梁侧面受拉纵筋中心处裂缝宽度的修正计算公式。文献[6]对重组竹梁进行了试验研究与模拟对比分析，发现该梁受压承载力稳定，试验结果与模拟结果拟合良好。文献[7]对干节点部分预应力混凝土连续梁力学性能进行了试验，验证了ANSYS软件对梁模拟分析的可能性。文献[8]对纤维增强泡沫混凝土(fiber-reinforced foamed concrete, FRFC)的钢-混凝土-钢(steel-concrete-steel, SCS)夹芯梁受弯性能进行了研究，证明采用FRFC有助于提高SCS夹芯梁的承载力和延性等性能。

通过文献分析发现：目前国内外对轻混凝土梁的研究多集中于混凝土骨料对梁本身性能的影响，通过采用轻质骨料来控制混凝土梁的自身质量，并在此基础上尽可能地提高其力学性能，但针对开孔或开多孔空心梁方面的研究相对较少。本文主要介绍在普通混凝土实心预制梁的基础上进行改进的一种新型双孔空心预制梁，即在普通实心预制梁的腹部沿纵向等间距对称开双孔。通过对新型双孔空心预制梁进行试验研究，了解其相关力学性能。

1 试验构件设计

图1 双孔空心预制梁示意图(单位：mm)

为了研究新型双孔空心预制梁的抗弯性能，共制作了3个试件，编号分别为L1-1、L1-2和L1-3。双孔空心预制梁示意图如图1所示。另外制作1根普通实心预制梁作为对照，编号为L2。两种预制梁底部均设置5根HRB335型直径为6 mm的纵向受拉钢筋。受拉钢筋的屈服强度为367.84 MPa，极限强度为485.63 MPa，弹性模量为2×105。梁截面尺寸均为120 mm×230 mm，计算跨长均为1 500 mm。空心预制梁为双孔对称等距开孔，开孔数为2，开孔直径为80 mm，孔间距为20 mm，各孔距截面两侧距离为25 mm。混凝土强度等级为C25，试件龄期为28 d，抗压强度试验值为27.6 MPa。以图1的构造为例，双孔空心预制梁与同尺寸实心预制梁相比，原材料的用量减少了36.41%，节约了材料，减轻了自身质量。

2 测点布置

位移计布置：为了测量新型双孔空心预制梁关键部位的变形，在试验构件上共布置了5个位移计，分别在梁跨中、梁1/4处和梁左右两端位置。试验装置图见图2，其中，梁底部的3个位移计主要采集新型双孔空心预制梁在荷载加载过程中的竖向变形，安装在左右两端的位移计可消除新型双孔空心预制梁试验变形误差，获得新型双孔空心预制梁的挠度曲线。另外，在试验过程中位移计表座均安装在可靠的约束支座上，防止外界不当作用对试验产生不必要的干扰。

应变片布置：为了测量双孔空心预制梁在加载过程中所对应的变形，在其跨中关键部位沿梁高方向等距布置5个混凝土电阻应变片，用来分析其变形规律，判断应变的变化规律是否满足平截面假定等。电阻应变片尺寸为5 mm×80 mm，电阻为120 Ω，具体位置和布置方式如图2所示。

荷载传感器布置：在液压千斤顶和分配梁之间固定一个荷载传感器，来实现试验过程中对荷载的控制。

1.反力架；2.液压千斤顶；3.加载梁；4.试件；5.应变片；6.位移计；7.支座；8.荷载传感器。

3 加载制度

双孔空心预制梁的抗弯性能试验采用两点加载方式[9]，在ZT-FY 30型的自平衡反力试验架上完成。反力架上加载器施加的荷载，由工字钢分配梁通过两根圆形滚轴平均分配到双孔空心预制梁上，并通过荷载传感器采用荷载控制级进行逐级加载。在整个试验过程中，通过数据记录仪实时采集施加荷载、挠度及微变形等相关试验数据。

试验加载按照GB/T 50152—2012《混凝土结构试验方法标准》[10]中的相关规定进行分级逐步加载。在加载初期，以3 kN为控制级进行加载，每级加载完成后保持2 min，待试件的变形基本趋于稳定，再进行下一级加载。加载至试件出现裂缝，改变加载制度，以1 kN为控制级进行加载至试件破坏。

4 试验过程及结果分析

4.1 试验过程描述及破坏形态

双孔空心预制梁和实心预制梁在加载过程和破坏形态上基本相似，下面主要以L1-1试件为例对试验过程进行讨论。在加载初期，由于施加荷载较小，无裂缝产生，此时，在受压区的混凝土处于弹性工作阶段，荷载-挠度曲线斜率呈线性变化，斜率数值较小且趋势平缓。随着荷载的增加，在跨中纯弯段受拉区的混凝土呈现明显的脆性，出现了首批裂缝。裂缝宽度较小，长度为2～3 cm，在纯弯段均匀分布，且与中和轴基本垂直，此时各挠度曲线出现突变，斜率增加，荷载突变值与试验记录的开裂荷载相近，约为9 kN。随着荷载继续增大，纯弯段裂缝增多，裂缝延伸至5～7 cm，形成主裂缝。在加载点附近也开始出现垂直裂缝，且各裂缝迅速延伸，此时受拉区部分混凝土已退出工作，荷载主要由钢筋和部分混凝土共同承担，荷载-挠度曲线呈非线性变化。在加载后期,裂缝宽度迅速增加，主裂缝宽度急剧增宽约1 cm，且几乎贯穿梁高，此时，受拉钢筋达到屈服状态，预制梁刚度迅速降低，挠度急剧增加，中和轴迅速上升，且受压区混凝土塑性特征明显。当荷载继续增加，承载力掉载明显，裂缝宽度加宽且长度增加。受压区混凝土逐渐达到最大压应变，最终被压碎，试验终止。

预制梁各试件破坏图如图3所示。由图3可以看出：双孔空心预制梁L1-1、L1-2、L1-3试件和实心预制梁L2试件破坏形式基本相同，在梁的跨中区域逐渐出现垂直裂缝。通过比较发现：双孔空心预制梁L1-1、L1-2和L1-3试件的裂缝相对较密且集中，分布较均匀，如图3a～图3c所示；实心预制梁L2试件的裂缝相对较少，并且较分散，如图3d所示。在裂缝开展过程中，实心预制梁L2试件在开裂后裂缝迅速延伸，数量少且较集中，在试验后期，主裂缝宽度虽有增加，但长度几乎不再增加，直到试件破坏。而双孔空心预制梁L1-1、L1-2和L1-3试件在加载的整个过程中，受力变形相对比较均匀，在破坏前裂缝长度和宽度均逐步延伸，且分布更加均匀。从整个破坏过程和破坏形态来看，双孔空心预制梁的受力变形能力与实心预制梁相比，表现出较好的优越性，对工程更有利。

(a) L1-1试件 (b) L1-2试件

图3 预制梁各试件破坏图

4.2 荷载-挠度曲线分析

图4 各试件荷载-挠度曲线

各试件荷载-挠度曲线如图4所示。图4中，“L1平均”为L1-1、L1-2和L1-3试件的平均荷载-挠度曲线。从图4中可以看出：实心预制梁和双孔空心预制梁的破坏过程均经历了3个阶段。

第1阶段：混凝土开裂。此时为试验开始阶段，构件刚度较大，试验荷载较小，随着荷载增加，构件挠度变化也较小；当荷载增大至某一数值时，受拉区边缘混凝土应变达到抗拉极限拉应变，混凝土开裂，荷载-挠度曲线出现第1个转折点[11]。此时，实心预制梁和双孔空心预制梁的挠度较为接近。

第2阶段：屈服阶段。此阶段受拉区混凝土裂缝随着荷载的增加而不断开展，部分受拉区混凝土退出工作，受拉钢筋和未退出工作的部分混凝土拉应力增大，出现了内力重分布现象[12]。构件刚度减小，挠度变化加大，直到受压区混凝土出现了局部被压碎现象，受拉区钢筋达到屈服状态。双孔空心预制梁的挠度大约为实心预制梁的2倍，可见此阶段双孔空心预制梁具有良好的受力变形性能。

第3阶段：破坏阶段。当受拉钢筋屈服后，随着荷载的增加，承载力增加不明显，但构件挠度迅速增大，裂缝迅速向受压区延伸，直至受压区混凝土被压碎，构件破坏。此时，两种预制梁的挠度达到极限，且较为接近。

在整个试验加载过程中，两种预制梁在第1阶段的变化规律基本相同，第3阶段达到破坏荷载时挠度也基本接近。但在第2阶段表现出较大的差别，实心预制梁的曲率远大于双孔空心预制梁。双孔空心预制梁的斜率在钢筋屈服前随着荷载的不断增加而逐渐减小，而实心预制梁的斜率在钢筋屈服前几乎不变，在钢筋屈服时才出现突变，达到屈服时两者挠度相差较大。

从图4中曲线来看，双孔空心预制梁的刚度随着荷载增加逐步退化，而实心预制梁的刚度在试件开裂后退化迅速。从荷载-挠度曲线的整体发展趋势来看，各双孔空心预制梁试件和平均值曲线与实心预制梁试件相比更为规整和平滑。说明梁开孔后在受力过程中改变了力的传递路径，在开孔部位减少了一部分混凝土的应力集中，有利于梁的整体受力和变形。

4.3 跨中截面变形分析

在钢筋混凝土受弯构件理论计算中，平截面假定作为基本假定被广泛接受，在现行规范中，受弯构件的计算理论也基本都以平截面假定为前提[13]。本试验通过在预制梁跨中混凝土表面布置应变片，测得预制梁在整个加载过程中应变随荷载的变化情况。

在不同荷载等级下，两种预制梁截面的应变变化规律基本相似，所以本文仅给出双孔空心预制梁L1-1试件和实心预制梁L2试件的荷载-应变曲线图，见图5。由图5可知：梁跨中截面混凝土应变沿截面高度呈线性关系，各位置的应变与该处到中和轴的距离呈正比，预制梁截面在不同荷载等级下保持为平面。在加载后期，由于受拉区混凝土大部分退出工作，荷载主要由受拉钢筋和少量混凝土承担，随着受拉钢筋的屈服，预制梁中和轴也大幅度上升，混凝土应变几乎呈直线发展，但应变整体仍呈现均匀变化的趋势。由此可见，开孔对梁截面应变规律影响不大，双孔空心预制梁截面应变的变化规律仍符合平截面假定[14]。

(a) L1-1试件 (b) L2试件

图5 L1-1试件和L2试件的荷载-应变曲线

4.4 承载力分析

各双孔空心预制梁和实心预制梁试件的主要承载力参数如表1所示。由表1可知：实心预制梁开裂荷载为6.7 kN，而开孔后的空心预制梁的平均开裂荷载为9.5 kN，相比实心预制梁提高了约41.79%，说明混凝土预制梁经开孔后延缓了梁的前期开裂，抗裂性能得到明显优化，这可能是因为空心预制梁的自身质量比实心预制梁轻。实心预制梁的破坏荷载为27.8 kN，空心预制梁的平均破坏荷载为25.4 kN，与实心预制梁相比降低了约8.63%，可见降低幅度并不是很大，说明混凝土预制梁虽然开了2个孔，导致最终破坏荷载降低，但对整体承载力影响并不大。

表1 预制梁主要承载力参数 kN

根据试验结果和各试件最终破坏形态，双孔空心预制梁和实心预制梁都是受拉钢筋屈服，受压区混凝土被压碎，破坏时均具备适筋破坏的特征，可以得出钢筋混凝土抗弯极限承载力计算理论同样适用于开孔后预制梁。根据GB 50010—2010《混凝土结构设计规范》[15]的规定，单筋受弯混凝土梁极限承载力计算公式为：

α1fcbx=fyAs；

(1)

Mu=fyAs(h0-x/2)，

(2)

其中：α1为受压材料的简化应力图形系数；fc为轴心抗压强度的设计值，H·mm-2；As为构件受拉钢筋的面积，mm2;fy为构件受拉钢筋的屈服强度，N·mm-2；x为受压区混凝土高度，mm；b为矩形截面宽度，mm；h0为截面有效高度，mm；Mu为极限弯矩，N·m。抗弯承载力计算简图见图6。

预制梁极限承载力的设计值和试验值见表2。由表2可知：双孔空心预制梁的极限承载力试验值比设计值提高了10%～14%，说明试验值相对较高，与设计值相比，不但能满足规范规定的基本要求，而且还有部分的储备，这对构件和整体结构来说是有利的。另外，预制梁开孔后的极限承载力比开孔前虽然出现了略微降低的现象，但仍能满足规范要求。实心预制梁L2试件极限承载力的试验值比设计值小0.4 kN，可能是由于构件在室外制作养护或运输过程中不当导致的，但对结果影响不大，误差仅为1.48%。可见，预制梁开孔后大大节省了材料和劳动力等工程成本，但极限承载力降低并不大，建议在工程中推广使用。

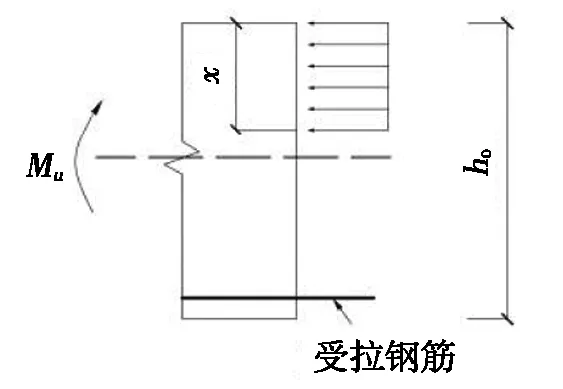
图6 抗弯承载力计算简图

表2 预制梁极限承载力的设计值和试验值

4.5 开孔对预制梁的影响分析

预制梁开双孔后，可以大大减少其自身质量，但对承载力的影响相对较小。主要原因在于：双孔空心预制梁虽然进行了有效开孔，但并没有改变原有的配筋形式和数量，改变和优化的仅仅是实心预制梁的构造形式。另外，传统实心预制梁传力路径是沿梁截面向下传递的，当在梁内部开孔后，其作用力经过开孔部位时，会绕过开孔并沿着梁截面两端两个半蝶形混凝土部分与两孔之间的蝶形混凝土部分共同协调进行传递，可见，传力路径也得到了重新规划与合理利用。

在裂缝开展和破坏形态方面，开孔后对预制梁整体的破坏形态影响并不大，但提高了梁的前期抗裂性能。双孔空心预制梁的开裂荷载与实心预制梁相比得到了明显提高，整体裂缝的开裂和发展变得更加均匀和平滑，改善了实心预制梁在屈服前期裂缝分布相对集中且易出现突变的状况。

在挠度方面，通过对两类预制梁的荷载-挠度曲线分析发现，开孔对预制梁达到破坏时的挠度几乎没有影响。但在开裂-屈服阶段，双孔空心预制梁达到屈服时的挠度远大于实心预制梁，挠度变化规律的区别也显著。开孔后的挠度发展基本呈现线性变化规律。随着荷载的增加，挠度变化趋于平缓。在实际工程中，有助于警示和帮助相关人员及时发现并解决存在的隐患。