基于二次微分的电力单相锁相环技术研究
2020-07-02张苏捷杨旭红张云飞潘鸿斌谢邦鹏
张苏捷, 杨旭红, 张云飞, 田 霆, 潘鸿斌, 王 珂, 谢邦鹏
(1.国网上海浦东供电公司,上海 200122; 2.上海电力大学,上海 200090)
在寻找克服世界能源危机的方法中,风力和光伏等分布式发电系统受到越来越多的关注[1]。单相并网逆变器作为分布式发电系统中能量转换和控制的核心,其性能直接影响和决定了整个并网系统的好坏。电网电压的相位、频率和幅值作为并网同步的关键信息,单相锁相环起着举足轻重的作用[2-4]。由于传统单相锁相环检测会在其输出的直流分量中产生大量的二倍频谐波,如果能够有效快速地消除二倍频分量,不仅可以精确检测单相交流信息的相位分量,还可以精确地实现有功功率和无功功率控制,从而有效提高电力系统的电能质量[5]。传统消除直流分量二倍频的方法是利用一个低通滤波器来滤除二倍频分量,并且低通滤波器的截止频率必须设计得很低[6]。从技术面上看,这样不仅大大增加了滤波器的设计难度,还在很大程度上影响了系统的动态响应特性[7-11]。因此,本文提出了一种新的消除二倍频方法,通过二次微分的原理,对锁相环输出的直流分量进行二次求导,然后再和开始的输出累加,这样就可以抵消输出的直流分量中所含有的二次谐波分量。如果采样频率取值较高时,两相邻时刻的电压采样值就可以简单地得到导数,其延时接近于零,且在电压的求导过程中可以用离散数字信号求差分来代替导数。本文提出的方法较传统采用低通滤波器的正交锁相环方法而言,具有设计简单、实时性强和动态性能好等优点。
1 传统的单相锁相环技术
图1是基于瞬时无功理论的单相锁相环系统的通用模型。对于该系统,一般采取与三相系统类似的锁相环控制方法,首先必须构造一个虚拟的两相正交静止坐标系。由于只有一个输入电压信号,因此需要构造出一个相位滞后90°的正交信号。产生正交电压相量的方法有很多,如将输入的电网电压信号延时 90°而生成对应的正交信号Uβ,但该方法延时时间稍长[12-13]。文献[14]利用二阶广义积分器的相移特性实现正交信号的生成。文献[15]利用有限冲击响应数字滤波器具有线性相移的特性,构造αβ静止坐标系下的正交电压矢量。这两种方法稳态性能好,但虚拟生成的Uβ会产生1/4个周期以上的延时,对锁相环动态性能会产生一定影响。这些方法中最易于实现的就是使用电网电压基波频率的延时方法,但也存在一些不足。
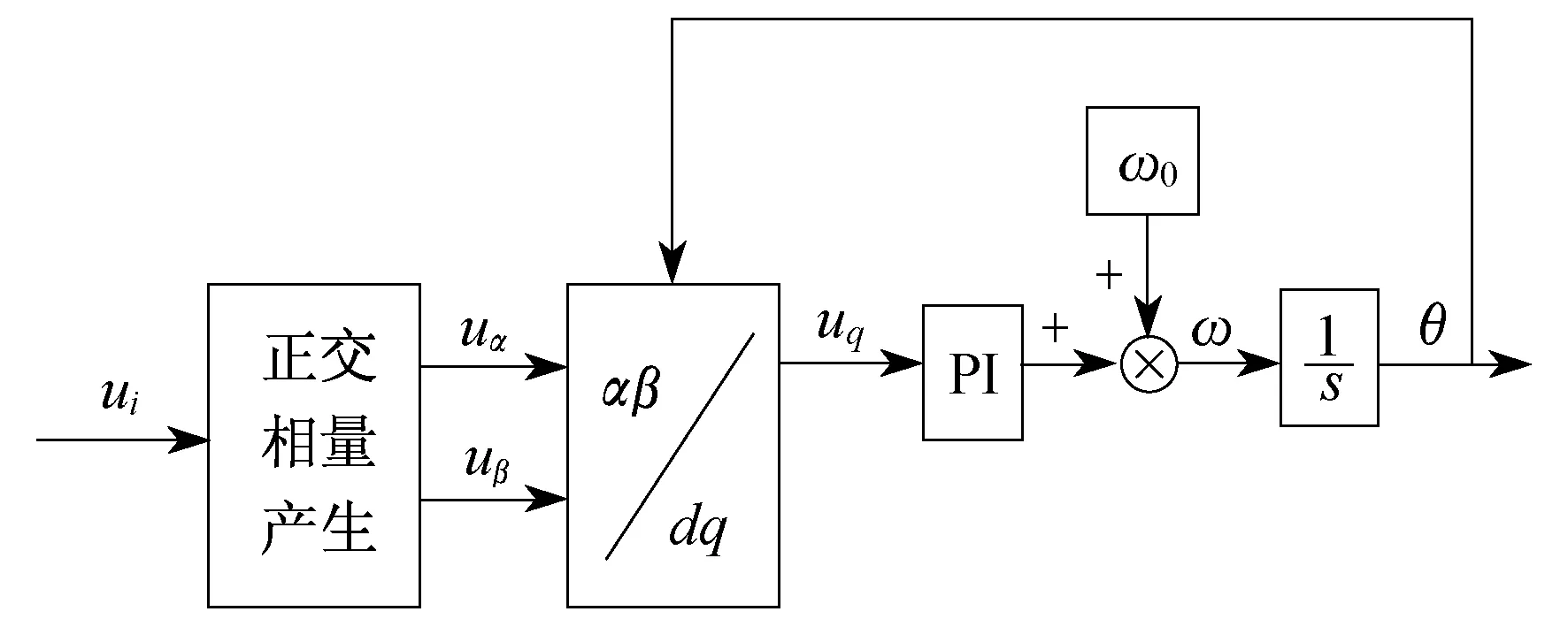
图1 传统单相锁相环系统的控制框图
2 二次谐波产生原因分析
由于移相带来的误差,虚拟正交的两相uα,uβ的夹角为90°+Δθ,其中Δθ很小,则可以得到
式中:θ——锁相环的输出相角。
图1中,αβ/dq变换公式如下
(3)
通过坐标变换可以得到
(4)
由于Δθ很小,故可以近似认为cosΔθ≈1,sinΔθ≈Δθ,从而得到
(5)
同理可得
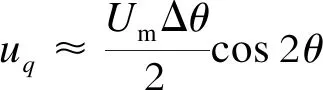
(6)
由上面的分析可以看出,经过αβ/dq变换后的结果除了无功有功直流分量外,还包含了二倍频的误差分量。由图1可以看出,二倍频分量经过PI调节器后会通过二次谐波的形式出现在锁相环的角频率ω中,从而使输出的相角θ出现偏差。这样对整个系统是非常不利的。
图2为传统消除锁相环二倍频分量方法的控制框图。在无功直流分量的输出前加一个低通滤波器(LPF),将无功直流分量中所包含的二倍频分量滤除。
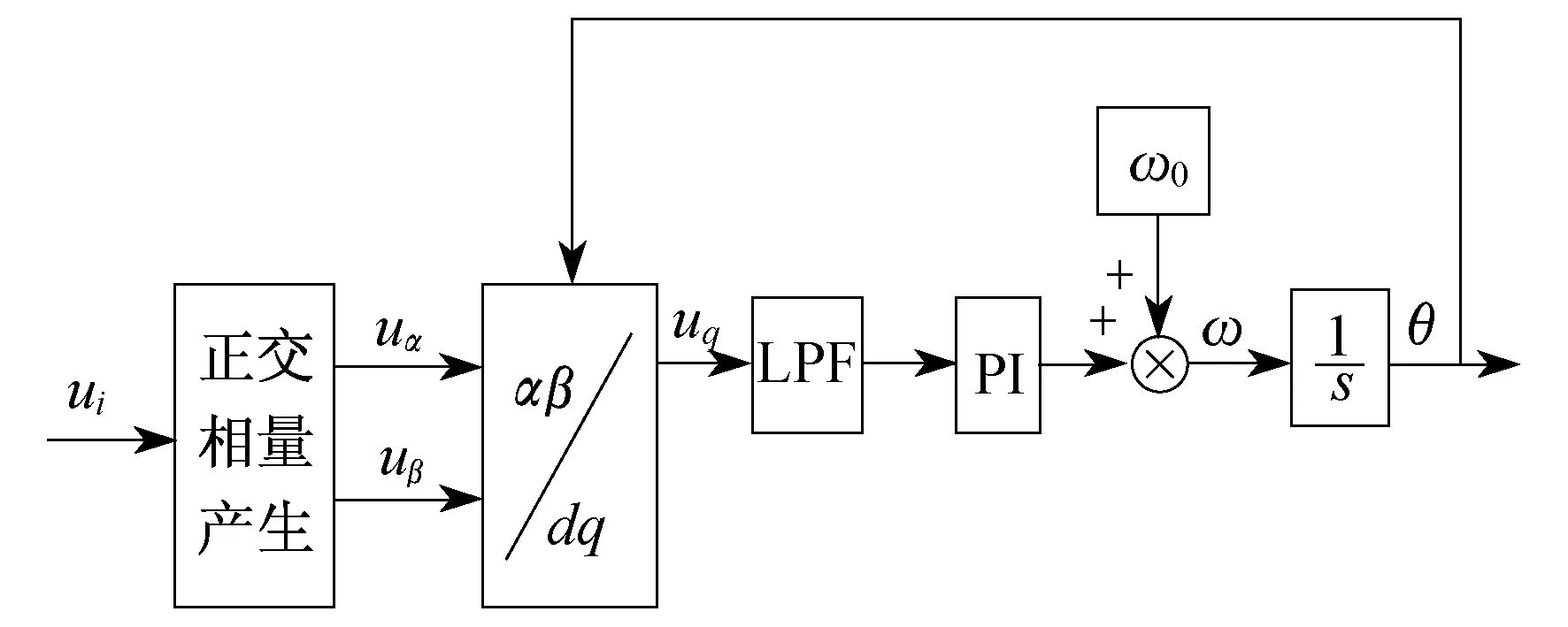
图2 采用低通滤波器方法的系统控制框图
3 基于二次微分的消除锁相环二倍频分量方法
通过上文的分析可知,增设低通滤波器可消除二倍频分量的影响,但是必须以牺牲动态性能为代价,因此用低通滤波器来消除锁相环的输出无功直流分量的二次谐波不是最好的选择。为了很好地滤除二次谐波,并且不影响系统的动态性能,本文提出了一种新的基于二次微分的消除锁相环二倍频分量方法。其系统控制框图如图3所示。
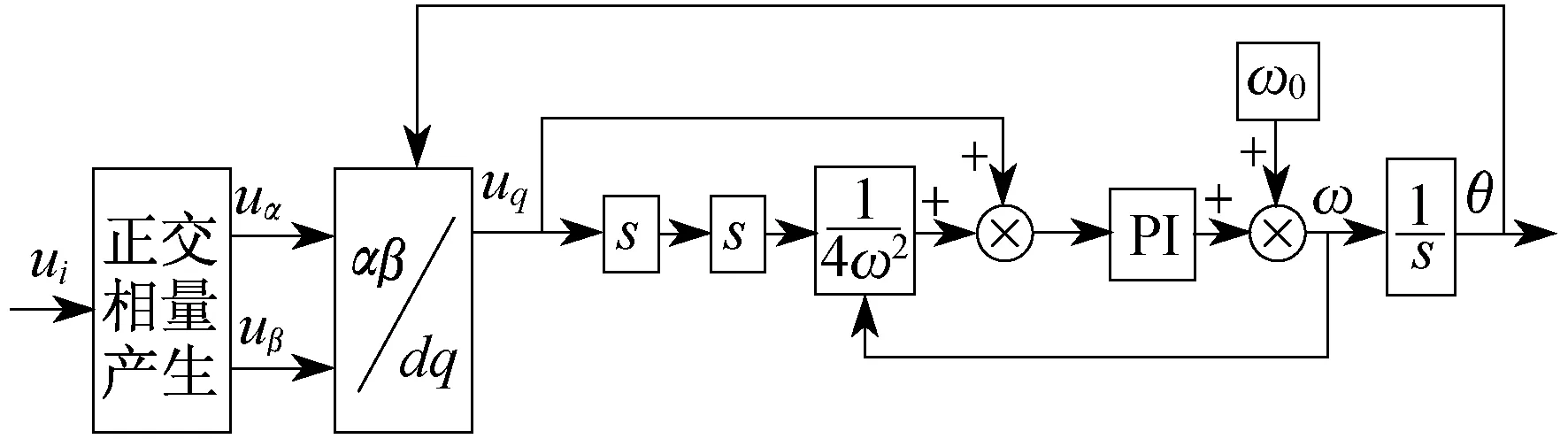
图3 基于二次微分的消除锁相环二倍频分量方法的系统控制框图
以有功分量ud为例,说明所提方法的原理。将式(5)经过一次微分后并乘以系数1/(2ω)可以得到
(7)
再将式(7)经过一次微分后并乘以系数1/(2ω)可以得到
(8)
其中,ω由锁相环输出反馈得到。
最后,把式(5)和式(8)相加可以得到
(9)
同理,将图3中的uq经过两次微分后并乘以1/(4ω2),最后与开始的输出累加就可以得到精确的输出结果。
通过该方法可有效地消除锁相环输出无功直流分量中所含的二倍频分量,使输出结果变得更加精确。
微分的实现方法就是求导。当采样频率较高时,利用两相邻时刻的电压采样值并根据微分的定义就可构造并得到其导数,其延时几乎接近于零。在实际计算过程中利用的是采样得到离散的数字量而不是连续的模拟量,可通过对离散数字信号求差分来代替求导数,则二次微分的实现如下
(10)
Δt较小时可取
(11)
设采样周期为Ts,则式(11)的Δt可以用Ts来表示,即
(12)
整理后可以得到
(13)
由式(13)可求得误差公式为
(14)
即
(15)
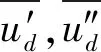
同理可得:
由此可知,在基波域内,该误差不随时间而改变,仅与采样间隔有关。这样,当采样频率较高时,Ts→0,则求导计算误差δ1,δ2趋向于零,说明差分代替倒数可行。该技术消除了二倍频,具备良好的实时性,解决了传统方法的延时问题。
4 仿真分析
本文利用PSIM软件搭建了传统锁相环电路,采用低通滤波器的锁相环电路以及采用二次微分的锁相环电路,通过仿真对提出的二次微分消除二倍频方法进行验证。
仿真电路中,输入的基波信号ui=100 cos 314t,波形如图4所示。将单相输入信号虚拟成正交的两相uα,uβ。设uα=ui,则生成的正交分量
(18)
uβ的波形如图5所示。
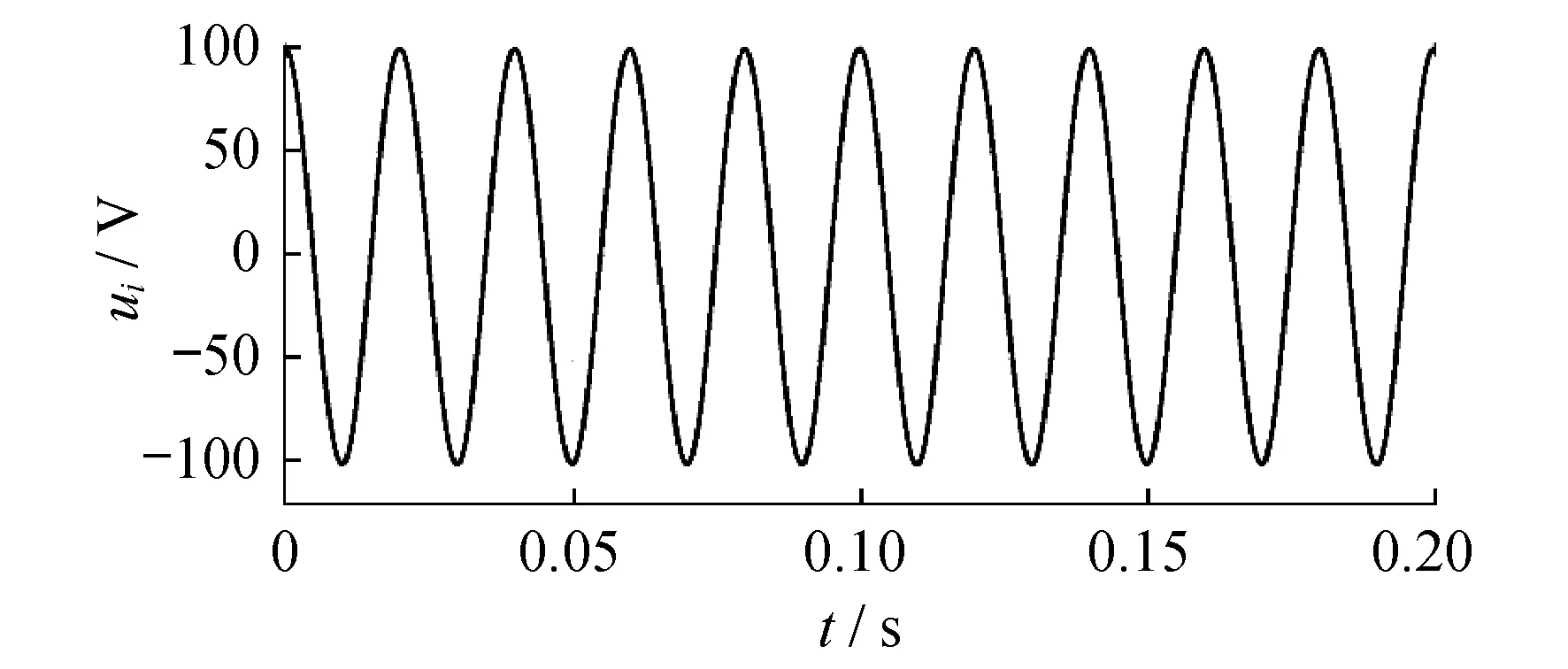
图4 输入的基波信号的波形
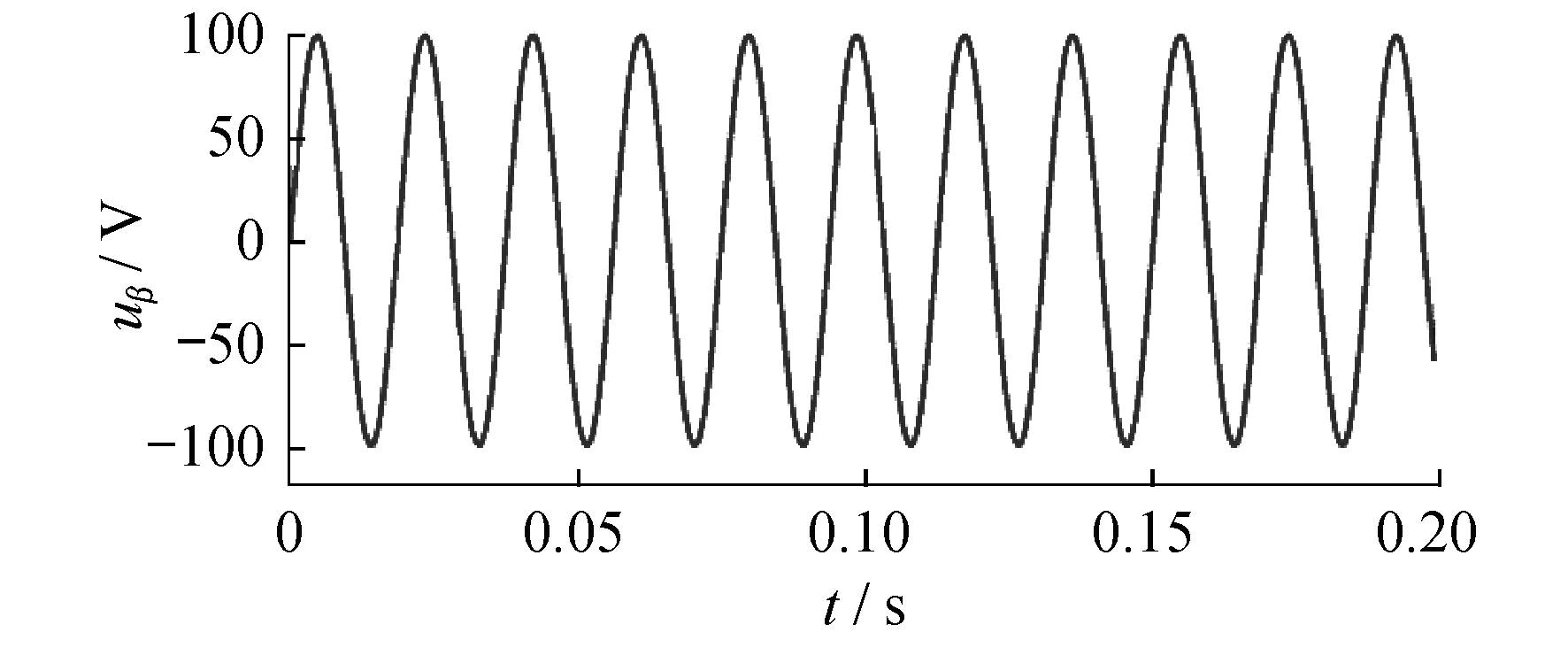
图5 虚拟构成的uβ的波形
输出的仿真波形如图6所示。从图6(a)可以看到,输出的直流分量都是带有毛刺的,经测量输出直流分量里面都包含有二倍频分量。
由图6(b)可以看到,采用低通滤波器的方法虽然能够滤除一定的谐波分量,但是很大程度上影响了系统的动态性能,uq和ud达到稳定的时间明显增加了很多。这说明要想滤除二倍频谐波分量,就必须把滤波器的截止频率设得很小,而滤波器的截止频率越小,系统的动态性能就越差,而且给滤波器的设计也带来了很大困难。
由图6(c)可以看到,该方法能很好地滤除锁相环输出直流分量中的二倍频谐波分量。与图6(a)相比,输出的直流分量中没有了毛刺,即不存在二倍频谐波分量;与图6(b)相比,输出的直流分量没有了延时,动态特性更好。
图7为分别采用低通滤波器和二次微分方法消除二倍频分量的电路输出结果比较。
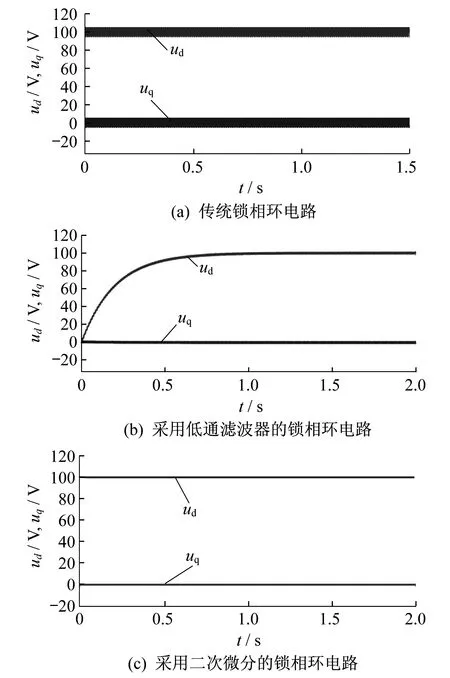
图6 3种电路输出的仿真波形
由图7可以看出:传统采用低通滤波器的方法虽然用了截止频率很低的滤波器但是还会存留很小的二倍频纹波;而采用二次微分的方法却几乎没有二倍频分量。这进一步说明了采用二次微分消除二倍频分量有更好的性能。
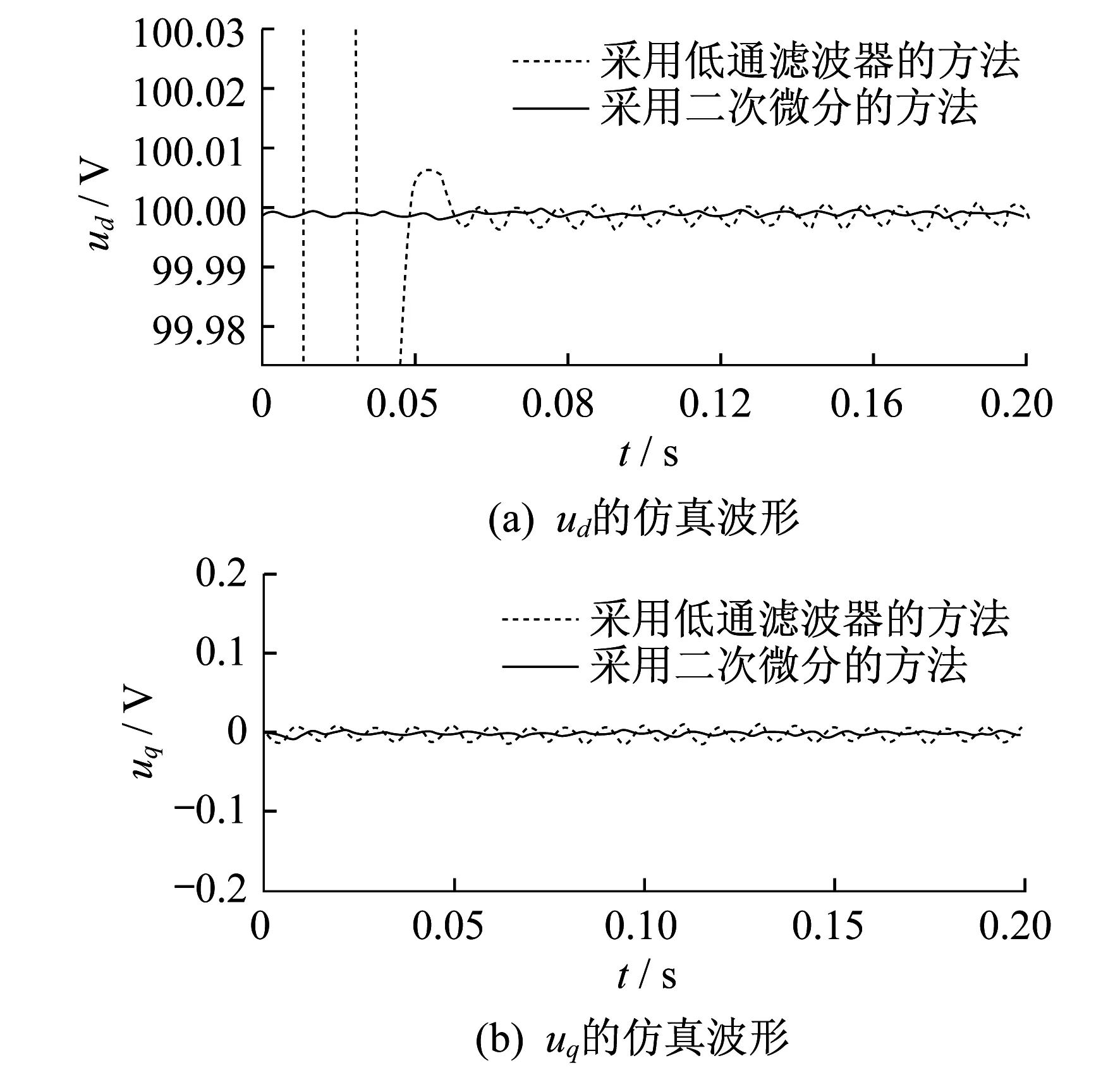
图7 2种方法输出结果的比较
5 结 语
本文针对传统单相锁相环电路中有功、无功直流分量的二次谐波通过低通滤波器难以完全滤除和系统动态特性较差的问题,提出了一种基于二次微分的单相锁相环技术。通过理论和仿真分析验证了所提方法的正确性和实用性。仿真结果表明,本文提出的采用二次微分的锁相环技术不仅消除了二倍频谐波问题,而且具有良好的动态性能和稳态精度。
