地球低轨道空间站往返月球的转移轨道设计

高永飞，王兆魁，张育林，

(1. 国防科技大学空天科学学院，长沙410073； 2. 清华大学航天航空学院，北京100084)

1 引言

国际空间站和即将建成的中国空间站都属于地球低轨道(Low Earth Orbit， LEO)空间站，作为载人航天的在轨空间资源，将支持航天员长期在轨驻留，提供在轨无重力科学实验环境，并释放微小卫星等，此外还可为各类飞行器提供在轨维修、加注等在轨服务[1]。 在基于地球低轨道空间站的载人月球探测飞行模式中，载人飞船从空间站出发飞往月球低轨道；航天员在完成月球探测任务后，从月球低轨道出发返回地球并借助大气减速再次停靠在空间站[2]。 由此可见，载人飞船在地月往返任务中，无论在奔月阶段还是返回地球阶段，都受到空间站轨道面的约束，而空间站轨道面约束无疑会对这类飞行模式中的轨道转移窗口产生影响。

研究人员对用于载人飞船地月转移[3]的一般地月转移轨道[4-7]、自由返回轨道[8-9]、混合轨道[10-11]和多段自由返回轨道[12]进行了较广泛地研究。 一般地月转移轨道仅需满足近地停泊轨道和近月距的约束[13-15]；自由返回轨道则不仅需要满足地球低轨道出发的约束，同时还需要满足近月距、再入大气的一系列约束条件；混合轨道拓展了自由返回轨道可达月球低轨道的范围；多段自由返回轨道在保证全过程自由返回特性的同时，拓展了可达月球低轨道的范围。 但目前的轨道设计方法都未涉及对地球低轨道空间站轨道面约束的处理，也未从轨道转移窗口、速度增量及转移时间等基本特征出发对基于地球低轨道空间站的载人月球探测飞行模式进行分析。

本文围绕地月/月地转移轨道受地球低轨道空间站轨道面约束的问题，基于圆锥曲线拼接模型和兰伯特问题，提出了相应的轨道设计方法。该方法首先通过解析求解地球低轨道空间站轨道面与月球影响球的交线，将空间站轨道面约束转化为用于求解地心段转移轨道的兰伯特问题；进而通过求解兰伯特问题得到了空间站轨道面约束下的地月/月地转移轨道；最后针对轨道转移窗口、速度增量、转移时间及可达月球低轨道分布等特征，对基于地球低轨道空间站的载人月球探测飞行模式进行了分析。

2 轨道设计模型

在轨道设计过程中，首先对地球低轨道空间站的轨道面约束在月球影响球处做几何分析，得到月球影响球入口点或出口点处的位置矢量，进而通过求解兰伯特问题得到地心段和月心段转移轨道的轨道根数，轨道设计流程如图1 所示。

图1 轨道设计流程图Fig.1 Flow chart of trajectory design

地月转移轨道的设计变量如下：①Rd为地月转移轨道近地点高度；②itl为地月转移轨道地心段轨道倾角；③ΩtlTd( ) 为地月转移轨道地心段轨道升交点赤经；④Td为地球低轨道空间站出发进入地月转移轨道的入轨时刻；⑤ΔTtl为地球低轨道空间站出发转移至月球影响球的转移时间；⑥为月心白道坐标系下Ts时刻的入口点纬度，其中Ts为到达月球影响球入口点时刻。

月地转移轨道的设计变量如下：①ite为月地转移轨道地心段轨道倾角；②Ωte为月地转移轨道地心段轨道升交点赤经；③γre为再入点航迹角；④Tre为再入时刻；⑤ΔTte为月地转移轨道地心段轨道转移时间；⑥为月心白道坐标系下{Rd，itl，Ωtl，Td，ΔTtl，}，轨道设计流程如下：Tse时刻的出口点纬度，其中Tse为月球影响球出口点时刻。

由于月地转移轨道的设计方法同地月转移相似，故以地球低轨道空间站出发到达月球的地月转移轨道为例介绍轨道设计方法。

在轨道设计过程中，Rd、itl、Ωtl由地球低轨道空间站轨道决定，存在关系如式(1)～(3)所示：

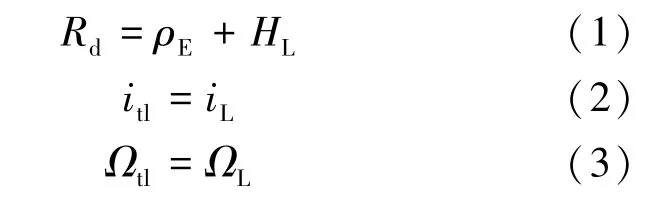
式中，ρE为地球平均半径，HL是空间站轨道高度，iL、ΩL分别为空间站轨道倾角及地月转移出发时刻的升交点赤经。 给定设计变量

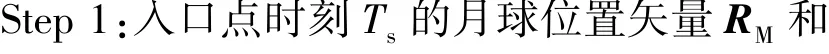
3 高精度动力学模型验证方法

4 转移轨道特征分析

式中，J2为地球扁率，iL地球低轨道空间站的轨道倾角，μE为地球引力常数，ρE为地球平均半径，aL为地球低轨道空间站运行轨道的半长轴。 进一步假设空间站轨道的升交点赤经在2025 00：00：00 TDT 时刻为0°；目标环月轨道的高度假设为200 ～220 km。 在月地返回停靠在地球低轨道空间站时，借助大气减速技术实现飞船的可重复使用，地球大气再入条件为γre＝- 5.2°和Hre＝120 km。

表1 地球低轨道空间站轨道参数及月球低轨道高度Table 1 Parameters of LEO space station and height of low lunar orbit

4.1 轨道转移窗口

4.1.1 地月转移

图4 分别给出了中国空间站和国际空间站出发到达月球低轨道的地月轨道转移窗口在2025 年的分布及窗口大小，其中红色曲线为轨道转移窗口的大小，蓝色曲线为相邻轨道转移窗口的时间间隔。 表2 给出了从中国空间站或国际空间站出发地月转移轨道的转移窗口统计值。 由表可知，从中国空间站或国际空间站出发的轨道转移窗口分别存在39 个和37 个，平均大小为1.608 8 天和1.656 1 天。 实际上，无论从中国空间站还是国际空间站出发，每月至少存在3 个轨道转移窗口，这主要由空间站运行轨道的运动所引起。

4.1.2 月地转移

图5 分别给出了2025 年从月球低轨道出发返回至中国空间站或国际空间站的轨道转移窗口分布及窗口大小，其中红色曲线为轨道转移窗口的大小，蓝色曲线为相邻轨道转移窗口的时间间隔。 表3 则给出了相应转移窗口的统计值。 由表可知，从月球低轨道返回至中国空间站或国际空间站的轨道转移窗口分别有39 个和37 个，平均大小分别为0.673 9 天和0.566 8 天；与地月轨道转移窗口相同，月地轨道转移窗口每月也至少存在3 个。

表2 2025 年地球低轨道空间站出发到达月球低轨道的轨道转移窗口统计值Table 2 Orbit transfer window statistics for mission from LEO space station to low lunar orbit in 2025

图4 2025 年地球低轨道空间站出发到达月球低轨道的轨道转移窗口分布及大小Fig.4 Orbital transfer window for the mission from LEO space station to low lunar orbit in 2025

4.2 速度增量及转移时间

4.2.1 地月转移

表3 2025 年月地转移返回至地球低轨道空间站的轨道转移窗口统计值Table 3 Orbit transfer window statistics for mission from low lunar orbit back to LEO space station in 2025

图5 2025 年月球转移返回至地球低轨道空间站的轨道转移窗口分布及大小Fig.5 Orbit transfer window for mission from low lunar orbit back to LEO space station in 2025

地月转移所需速度增量包括两部分：地球低轨道空间站出发进入地月转移轨道所需的速度增量Δvtl和到达月球附近时制动进入月球低轨道所需的近月制动速度增量ΔvLOI。

图6 给出了2025 年中国空间站和国际空间站出发到达月球低轨道所需的速度增量及转移时间，图中颜色条为转移轨道的相应转移时间。 由图可知，速度增量呈现周期性的波动形态，不同轨道转移窗口中所需的速度增量最小值具有约80 m/s的差异。 同一轨道转移窗口中，实现地月转移所需的速度增量介于3 845 m/s 和4 250 m/s之间，其对应的转移时间介于2.5～4.7 天。

2025 年，对于中国空间站出发的月球探测任务，其所需的最小速度增量为3 840 m/s，对应的转移时间为4.84 天，最大速度增量为4 233 m/s，对应的转移时间为2.48 天；对于国际空间站出发的月球探测任务，其所需的最小速度增量为3 848 m/s，对应的转移时间为4.82 天，最大速度增量为4 289 m/s，对应的转移时间为2.47 天。

4.2.2 月地转移

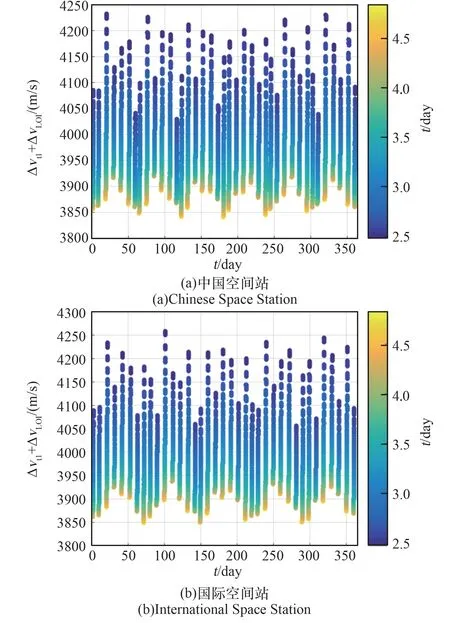
图6 2025 年地球低轨道空间站出发到达月球低轨道所需的速度增量和转移时间Fig.6 Velocity increment and time of flight for mission from LEO space station to low lunar orbit in 2025

在讨论载人飞船从月球低轨道返回至地球低轨道空间站时，本文提出借助地球大气减速实现载人飞船的近地制动，故月地转移所需速度增量仅包括从月球低轨道出发进入月地转移轨道所需的速度增量Δvte。

图7 给出了2025 年月球低轨道出发返回至中国空间站和国际空间站所需的速度增量及转移时间。 与地球转移速度增量类似，月地转移所需速度增量同样存在周期性波动，不同轨道转移窗口中所需的速度增量最小值具有约80 m/s 的差异。 同一轨道转移窗口内，速度增量介于760 m/s和1 100 m/s 之间，转移时间介于2. 5 ～4. 7 天。

具体的，在2025 年返回中国空间站的月地转移最小速度增量为761 m/s，其相应的转移时间为4.82 天，最大速度增量为1 098 m/s，其相应的转移时间为2.48 天；对于返回至国际空间站，月地转移所需的最小速度增量为764 m/s，其相应的转移时间为 4.82 天； 最大速度增量为1 113 m/s，相应的转移时间为2.46 天。

图7 2025 年月球低轨道出发返回至地球低轨道空间站所需的速度增量和转移时间Fig.7 Velocity increment and time of flight for mission from low lunar orbit back to LEO space station in 2025

4.3 地球低轨道空间站约束下的月球低轨道特性

为节省燃料，月球低轨道与月面之间的往返飞行采用共面上升与下降方式，故而地月转移可达的月球低轨道或月地转移的出发轨道决定了月面的可达范围。 例如，零倾角月球低轨道仅能支持月球赤道附近的探测任务；极轨月球低轨道则能够支持全月面的探测任务。 因此，本文针对基于地球低轨道空间站的载人月球探测飞行模式，分析可达月球低轨道与出发月球低轨道在月固坐标系下的轨道倾角-升交点经度范围。 这里选择月固坐标系，主要考虑到月球始终只有固定半个球面面向地球，月固坐标系相对于地球和月球的位置关系基本保持不变。

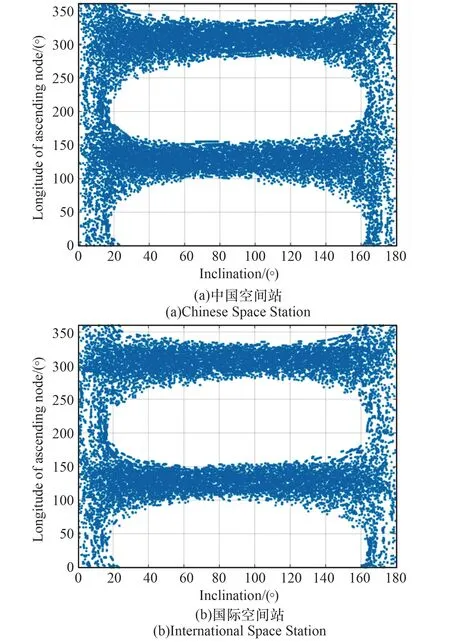
图8 2025 年地球低轨道空间站出发实现地月转移的可达月球低轨道Fig.8 The accessible lunar orbit from LEO space station in 2025

4.3.1 可达月球低轨道图8 分别给出2025 年地球低轨道空间站出发实现地月转移的可达月球低轨道在月固坐标系下的分布。 其中横坐标为轨道倾角，纵坐标为升交点经度。 由图可知，从中国空间站或国际空间站出发的地月转移轨道可以到达任意轨道倾角的月球低轨道；可达月球低轨道的升交点经度受到限制。 具体而言，从地球低轨道空间站出发，若要转移至极月球低轨道，则其升交点经度被限制在100°～150°或280°～330°的范围内。

另外，对比图8(a)和图8(b)可知，可达月球低轨道在月固坐标系下具有相似的轨道倾角-升交点经度分布。

4.3.2 出发月球低轨道

图9 分别给出了2025 年返回至中国空间站和国际空间站的出发月球低轨道在月固坐标系下的轨道倾角和升交点经度分布，其中横坐标为轨道倾角，纵坐标为升交点经度。

由图可知，任意轨道倾角的出发月球低轨道都可以返回至中国空间站或国际空间站。与可达月球低轨道相似，出发月球低轨道的升交点经度同样受到约束。 例如，从极月球低轨道出发返回至地球低轨道空间站，月球低轨道的升交点经度被限制在25°～75°或205°～255°的范围内。

对比图9(a)和图9(b)可知，无论返回至哪类地球低轨道空间站，出发月球低轨道的轨道倾角-升交点经度具有相似的分布。

4.4 高精度动力学模型修正结果

参考阿波罗飞船[17]的阻力系数CD＝ 1.289 1，地月转移面质比S/m( )LM＝2.9×10-4，月地转移面质比S/m( )ML＝2×10-3，表4 和表5 分别给出了中国空间站和国际空间站往返月球转移轨道的高精度动力学模型修正结果。 由表可知，高精度动力学模型下的转移轨道同圆锥曲线拼接法得到的转移轨道具有较小的差异，利用高精度动力学模型可有效针对轨道面约束下的初始轨道设计结果进行修正。

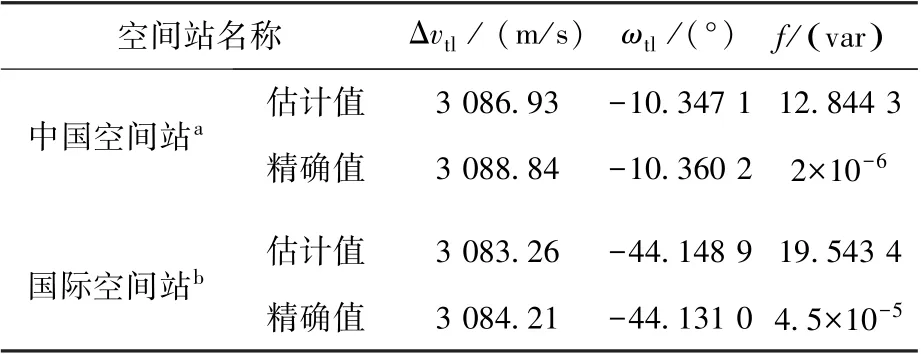
表4 地球低轨道空间站出发到达月球低轨道的参数修正结果Table 4 High-fidelity verification for mission from LEO space station to low lunar orbit

5 结论

1)分析表明中国空间站或国际空间站与月球低轨道之间的往返转移存在轨道转移窗口，且每月至少存在3 个。

2)空间站的轨道倾角不影响速度增量与转移时间；不同轨道倾角空间站的约束下，可达月球低轨道以及出发月球低轨道在月固坐标系下的轨道倾角-升交点经度分布类似。

3)高精度动力学模型下的模型验证表明初始轨道设计值与高精度动力学模型修正值仅有较小的差异。

表5 月球低轨道返回至地球低轨道空间站的参数修正结果Table 5 High-fidelity verification for mission from Low Lunar orbit back to LEO space station

4)本文提出的空间站往返月球低轨道的转移轨道设计方法将为基于地球低轨道空间站的载人月球探测飞行模式提供轨道设计的技术途径，特征分析结果也将为该模式提供可行的理论依据。

5)基于地球低轨道空间站的载人月球探测飞行模式相较于近地轨道一次对接或阿波罗直接登月模式，虽在轨道转移窗口方面受到限制，但其支持载人飞船的可重复使用，可充分发挥空间站的在轨服务能力，为未来地月空间的商业化开发提供了可行方案。