面向机械臂遥操作的虚拟人机交互系统设计

曾 欣，宋爱国∗，周永辉，李会军

(1. 东南大学仪器科学与工程学院，南京210096； 2. 北京空间飞行器总体设计部，北京100094)

1 引言

空间站机械臂是集空间感知、机动性和操作能力于一身的大型空间设备[1]，在空间站建设、在轨任务执行、观测检查，故障维修等方面发挥了重要的作用[2]。 传统的机械臂控制系统通过图像回传和按键式控制面板、手柄等设备对机械臂进行控制。 这些控制系统依靠视觉图像技术向操作者反馈机械臂的控制状态，缺乏力觉反馈[3]，容易受到舱外环境的遮挡影响，系统的安全性和可靠性较低，难以完成精细的操作任务[4]。

力反馈技术通过在机械臂上集成测力传感器，利用力反馈设备将机械臂采集到的接触力信息反馈给操作者，为操作者提供逼真的力觉临场感[5-6]，是空间站机械臂遥操作系统的关键技术。通过力反馈设备来控制机械臂，搭建具有力觉反馈的高临场感空间站机械臂遥操作控制系统，融合视觉、听觉、力觉等多种感官反馈信息，从而增强人机耦合度和人机协同操作的精度，可以帮助操作者更加快速、准确地控制机械臂，完成舱外操作任务[7]。

NASA 开发了机器人航天员R2 系统[8]，航天员利用数据手套等力反馈设备进行遥操作，并通过该系统成功捕获了一个在国际空间站实验舱内自由漂浮的物体[9]。 力反馈数据手套等设备可以控制远端机器人的运动姿态并反馈远端的接触力感给航天员，但数据手套的反馈力较小，穿戴繁琐，通用性不高[10]。 Force Dimension 公司研制了基于Delta 结构的Delta、Omega、Sigma 系列力反馈手控器[11]，最大可达7 个自由度，结构稳定，具备抓取操作自由度，但其运动空间和反馈力较小，适合在虚拟手术和虚拟游戏中应用。 韩国Kyungnam 大学Vu 等[12]针对遥操作系统设计了新型六自由度力反馈装置，设备采用六连杆并联结构，具有低惯性、大扭矩的特点，具有高度临场感，但机构耦合度高、解算复杂、控制难度大，并缺乏夹取自由度。 日本名古屋大学Arata 等[13-14]设计了DeltA-4 冗余式手控器，与Delta 机构相比，提升了工作空间范围，在反馈力和操作性能方面有较大的优势，但机构耦合度高、解算复杂度高。国内邓乐等[15]设计了六自由度力反馈手控器，采用液压驱动的方式，具有较大的刚度和较高的承载能力，动力性能比较好，但游隙非线性特性容易产生系统振荡的问题。 秦欢欢等[16]设计了双手混联式力反馈手控器，通过双手协同操作扩展了手控器任务的多样性，但占地面积较大，缺乏对不同材质的辨识。

综上，需要设计一种机械耦合度低、力反馈性能高、具有抓取自由度、对不同材质辨识度高的力反馈设备，以提升空间站机械臂控制系统的精确性、安全性和稳定性。 本文面向空间站机械臂遥操作控制，提出一种基于混联式七自由度力反馈手控器的虚拟人机交互系统方案，并完成了相关性能试验。

2 系统机构设计

混联式七自由度力反馈手控器的机械结构如图1 所示，力反馈手控器由平行连杆结构、菱形拉伸结构、末端三维旋转手柄、支架、配重块、手指扳机结构、直流伺服电机及绝对值编码器组成。

图1 混联式力反馈手控器组成Fig.1 Configuration of hybrid force feedback hand controller

操作人员的手固定在末端手柄处，编码器实时采集手控器各个自由度的角度信息，并传递给系统控制箱；电机采用Maxon 公司RE 系列312970 型稀有金属电刷直流电机，该型号电机具有良好静态性能以及散热能力，适用于低速大转矩的力反馈设备；配重块用于保持手控器平衡；手控器通过平行连杆结构、菱形拉伸结构和末端三维转动结构相串联，实现了三维平动自由度和三维转动自由度的机械解耦，降低了解算的复杂度和控制难度。 混联式设计能够在较大的工作空间内保证足够的刚度以及输出能力。

3 系统运动学分析

3.1 平动机构

对操作人员手部的位置和姿态进行精确跟踪是手控器的主要性能之一，也是遥操作任务精确控制的重要保障[17]。 图2 是力反馈手控器平动结构原理图，力反馈手控器通过将菱形拉伸结构串联安装在平行连杆结构的末端平面上，实现空间中的三维平动，并可以保证图中3个平面永远保持平行，不会耦合多余的转动自由度，其末端位置为菱形拉伸结构末端平面的中点O2。 平行连杆结构和菱形拉伸结构有3 个运动自由度，分别绕轴1、轴2 和轴3 转动。 力反馈手控器末端位置的正向求解过程就是在已知绕轴1、轴2 和轴3 转动角度的情况下，求解点O2在空间中的位置。

图2 平动结构原理图Fig.2 Schematic diagram of the translation structure

设平行四连杆杆长均为L1，菱形拉伸结构杆长均为L2，平行连杆结构中点为原点O，z轴垂直于平面ABCD向外为正方向。 为方便描述，设平行连杆绕轴1、轴2、轴3 旋转的角度分别为α、β、γ，顺时针方向为正方向。 手控器初始位置为平行连杆机构与平面ABCD垂直，菱形拉伸结构的初始位置沿z轴负方向压缩到底，由于存在机械限制，令菱形机构初始角度为γ0。

平行连杆机构的末端点O1的运动轨迹是原点为点O， 半径为L1的球形弧面，又因为面A1B1C1D1与面A2B2C2D2平行，所以手控器末端O2点与平动机构末端O1点的x、y轴坐标相同，末端O2点x、y轴的坐标可以通过OO1与轴1、轴2转动的角度α、β的几何关系进行求解。

如图3 所示，当平动机构末端O1点位于空间任一位置时，手控器末端O2点x、y轴坐标如式(1)所示：

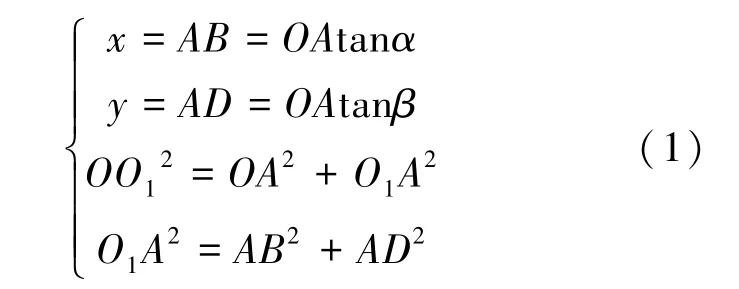
由于平动机构末端在x、y轴方向上的运动轨迹呈球面，会导致手控器末端位置沿着z轴负方向发生一定移动。 为避免x、y轴方向上的运动对z轴位置解算产生耦合影响，手控器末端O2点的z轴坐标采用相对于O1的坐标，而x、y轴的位置采用相对于原点O的坐标。 由于平面A1B1C1D1与平面A2B2C2D2相互平行，通过轴3转动的角度γ和菱形结构的几何关系可以得到z轴的坐标。

图3 位移计算示意图Fig.3 Schematic diagram of displacement calculation

由上述分析可解得手控器末端O2的位置坐标为式(2)：

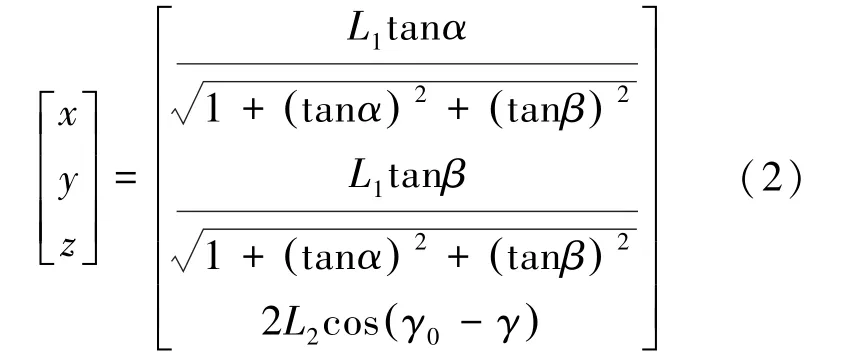
其中α∈(-45°～45°)、β∈(-45°～45°)、γ∈(0°～80°)、γ0＝80°。

由于建立的理想几何模型与真实机械结构的参数存在一定误差[18]，可以通过逆向解算的方式，利用高精度三维电动滑轨对位置计算公式做进一步标定修正，以消除机械结构参数造成的公式参数误差。 测试前需对手控器的位置零点与电动滑轨的位置零点进行标定，以消除标定过程中手控器与电动滑轨的相对位置误差。 由式(2)可知，角度α、β、γ由高精度的绝对值编码器测得，末端位置x，y，z( ) 由高精度三维电动滑轨测得，其精度远高于手控器要求的精度，在经过位置零点标定后，可认为位置解算误差主要来自于手控器平行连杆结构杆长L1、菱形拉伸结构杆长L2以及菱形初始角度γ0。 通过逆向解算将测得的真实角度值和末端位置值代入式(2)中求解，可得到实际值L1real、L2real、γ0real。

首先求解L1real，利用电动滑轨在x或者y轴上带动手控器进行移动，直至手控器位置极限。以x轴为例，在运动范围内等间距取线性度较好的三点x1、x2、x3， 将对应的α、β角度值带入式(2)得到方程组(3)，对式(3)进行求解，取L1的平均值可得实际值L1real。

然后求解L2real、γ0real，在z轴运动范围内等间距取线性度较好的3 点z1、z2、z3， 将对应的γ角度值带入公式(2)得到方程组(4)，求解该方程组可以求得L2、γ0的实际值L2real、γ0real。

将经过逆向标定后的真实参数重新带入位置解算公式(2)，得到最终的位置解算公式(5)：

3.2 转动机构

图4 为手控器末端转动机构原理图，转动机构串联安装在平动机构的末端平面上，保证了转动部分不会耦合多余的平动自由度。 转动机构俯仰轴、偏航轴和横滚轴两两相互垂直并相交于一点，所以转动自由度相互之间不会发生耦合。

操作者握住末端手柄进行操作，手部的三维旋转角度直接由俯仰轴、偏航轴和横滚轴旋转的角度直接获得。 手柄还配有符合人机功效学的手指扳机结构，用于控制虚拟夹具的开合，其开合角度也可由扳机旋转的角度获得。

4 系统静力学分析

图4 手控器转动结构原理图Fig.4 Schematic diagram of the rotation structure of hand controller

获得手控器末端需要反馈的力与力矩后，需逆向求解每个电机的控制参数，从而驱动手控器输出相应的反馈力。 力反馈手控器通过串并联相结合的机构设计，实现了力与力矩的解耦，即只需要求得对应自由度的力臂大小。 如图2 所示，手控器产生的平动力矩由直流电机1＃、2＃、3＃提供，设为τ1、τ2、τ3，点O2与面ABCD在z轴方向的垂直距离为X、Y轴电机的力臂大小。 而z轴采用虚位移原理进行分析，可以解得手控器平动力为式(6)：

如图4 所示，手控器产生的转动力矩由安装在转动机构俯仰轴、偏航轴和横滚轴三轴上的直流电机4＃、5＃、6＃提供，设为τ4、τ5、τ6， 其力臂长度与机构设计参数决定，几乎不变，可由机械参数获取到，设其力臂长度分别为L4、L5、L6。 手指扳机结构的力矩由扳机上的电机7＃提供，设为τ7，其力臂为L7，通过公式F＝τ/L即可求得施加给操作人员的转动力。

5 控制系统

手控器系统控制模块包括位置检测模块、电源模块、微处理器模块、以太网模块、触摸屏模块及电机驱动模块，系统框图如图5 所示。

图5 控制系统框图Fig.5 Block diagram of the control system

力反馈手控器各自由度转动的角度通过安装在转动轴上的绝对值编码器进行测量，通过FPGA 并行读取，并由微处理器模块解算成末端位置数据。 微处理器模块将位置数据发送到触摸屏和计算机的上位机中，实现手控器的位置捕获与数据传输。 计算机中的虚拟场景软件计算反馈力大小，并将反馈力数据发送回微处理器模块。 由FPGA 产生对应的PWM 波控制信号并发送给电机驱动模块，驱动手控器各自由度电机输出反馈力矩。

理想的直流电机的电磁转矩仅与电枢电流和气隙磁通成正比，而气隙磁通一般为定值，所以直流电机驱动转矩与电枢电流呈线性关系[19-20]。由于手控器主要工作在低速状态，惯性转矩较小，可以忽略。 而空载转矩为定值，并且力反馈手控器的对力输出的精度要求不高，所以可以通过稳定控制电枢电流的方法来实现扭矩的控制输出。

控制系统利用电流传感器对输出电流进行采样，利用编码器采集速度和位置，搭建位置-速度-电流串级PID 算法，实现了对输出电流、运动速度、末端位置的闭环控制，从而实现了对末端输出反馈力的稳定控制。

6 系统试验与标定

6.1 位置精度测试

为了验证人机交互系统的正向位置求解精度，使用高精度三维电动滑轨对力反馈手控器x、y、z三轴进行位移测试。 如图6 为标定系统组成图。

图6 标定系统组成 Fig.6 Configuration of the calibration system

首先测量力反馈手控器的工作空间，将力反馈手控器末端三维旋转手柄卸除，将菱形结构末端平面固定在三维电动滑轨y轴平面上。 仔细调整电动滑轨位置至手控器的位置零点处，确保手控器平行连杆结构垂直于电动滑轨y轴平面，菱形拉伸结构的初始位置沿z轴负方向压缩到底，调整完成后，将电动滑轨位置归零，使得手控器和电动滑轨之间无相对位置误差，然后利用电动滑轨带动手控器末端分别沿x、y、z三轴运动到手控器工作空间的极限位置，记录极限位置的电动滑轨的坐标。 试验结果如表1 所示，力反馈手控器的工作空间略大于250 mm × 250 mm × 250 mm。

表1 手控器末端实际运动范围Table 1 Actual movement range of the hand controller end

在工作空间范围内，进行力反馈手控器位置跟踪精度测试。 试验起始点与工作空间测试相同，将电动滑轨零点位置调整至手控器零点位置处，利用三维电动滑轨带动手控器末端以1 mm的步距在x、y、z三轴上，从起点到工作空间极限位置进行一次往返位移。 共进行3 次测试，取3次测试数据的平均值作为测试结果。 因为手控器工作空间是对称的，只需对x、y轴进行正方向往返方向测试即可，即位置精度测试范围为x轴：0～125 mm，y轴：0～125 mm，z轴：0～250 mm。

利用经过标定修正，消除了机械误差的位置解算公式对手控器末端进行解算，得出手控器位置数据，并与三维电动滑轨的位置数据进行比较，可计算出本系统中手控器的位置跟踪精度。

力反馈手控器各轴位置跟踪精度标定结果如图7～图9 所示。 手控器x轴(图7)3 次往返测试的平均位置误差为0.01 mm， 最大误差为-0.59 mm，误差方差为0.034 mm2。 手控器y轴(图8) 3 次往返测试的平均位置误差为0.012 mm，最大误差-0.478 mm，误差方差为0.035 mm2。 手控器z轴(图9)3 次往返测试的平均位置误差为-0.21 mm，最大误差-0.58 mm，误差方差为0.051 mm2。 结果表明，经过标定后，双手装置三轴的位置跟踪误差小于0.6 mm。

图7 x 轴位置跟踪精度 Fig.7 Accuracy of position tracking in x-axis

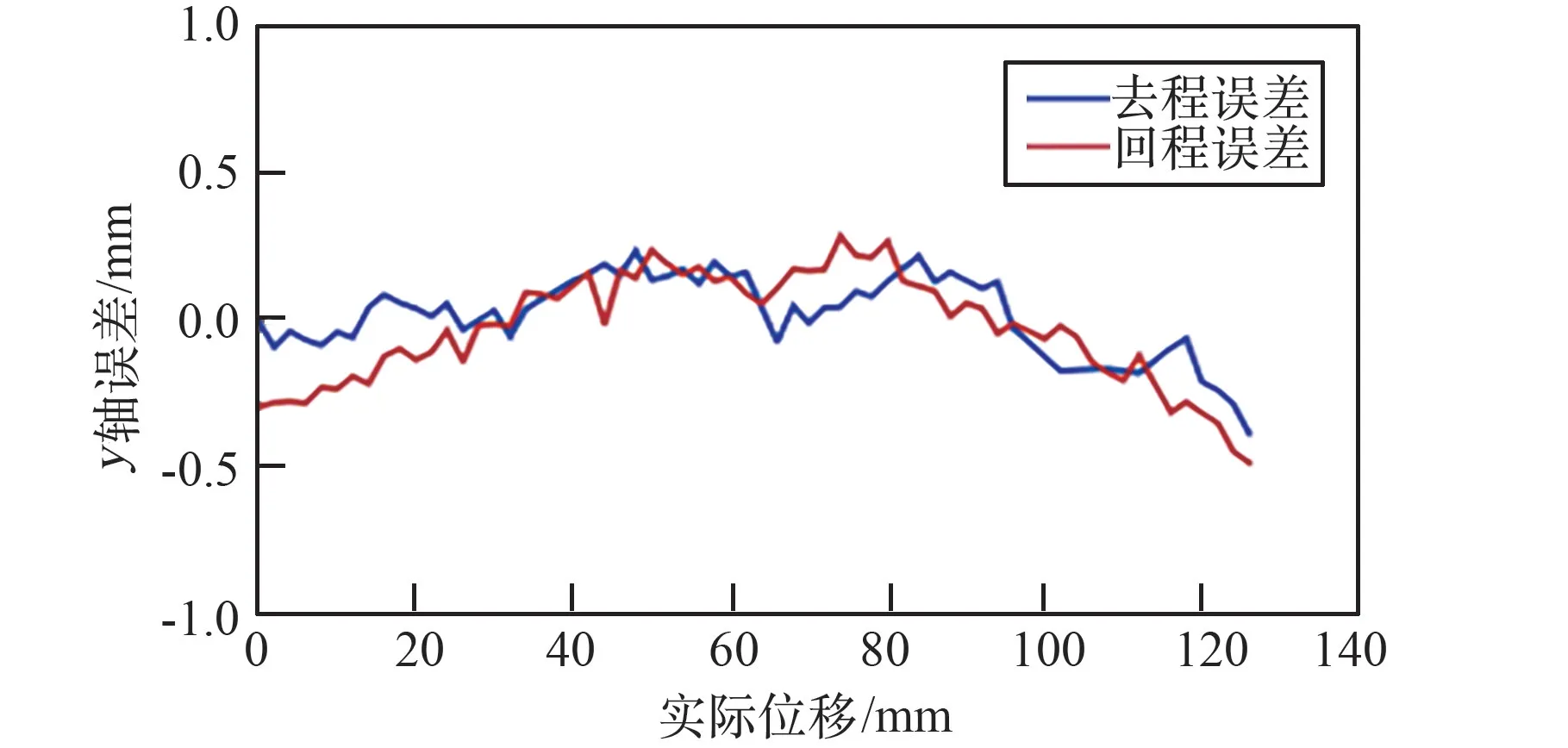
图8 y 轴位置跟踪精度 Fig.8 Accuracy of position tracking in y-axis

图9 z 轴位置跟踪精度 Fig.9 Accuracy of position tracking in z-axis

6.2 输出力性能测试

力反馈手控器的输出性能可以利用三维电动滑轨和六维力测量装置进行测试(图10)。 六维力装置内置6 个单向的压力传感器，固定在三维电动滑轨轴上，力反馈手控器菱形结构末端平面固定在六维力传感器装置之中，通过给力反馈手控器施加电流信号，可由末端的六维力传感器装置的上位机读取出末端的三维平动反馈力大小。

图10 输出力测试装置Fig.10 Test device for output force

通过控制箱给手控器输入电机最大工作电流作为参考电流信号，利用六维力传感器装置记录手控器末端三轴的输出力情况，共进行了3 次试验。 试验表明：力反馈手控器末端x轴3 次稳定输出力分别为16. 62 N，16.57 N，16.63 N，平均输出力为16.60 N。y轴3 次稳定输出力分别为16.23 N，16.17 N，16.21 N，平均稳定输出力为16.20 N。z轴3 次稳定输出力分别为15. 55 N，15.52 N，15.56 N，平均稳定输出力为15.54 N。综上，力反馈手控器末端输出力可达15 N。

6.3 系统交互性能测试

为验证人机交互系统对机械臂控制的性能，系统利用CHAI3D 平台设计了虚拟夹取物块试验场景(图11)。 虚拟场景中有3 种不同材质的物块和一只虚拟手，操作者通过手控器控制虚拟手的移动、旋转、张开与闭合，模拟虚拟机械臂的夹取动作。

图11 虚拟夹取试验场景Fig.11 Experiment scene of virtual clamping

虚拟场景中的物体采用沿坐标轴包围盒AABB 碰撞检测算法[21]进行碰撞检测，该算法具有计算时间短且检测精度高的特点。 虚拟场景采用基于God-Object 算法[22-23]来计算虚拟代理与虚拟物体发生接触后的相互作用力，由于力反馈手控器自由度有限，难以反馈模拟面接触时的触感，所以在虚拟场景中虚拟手的触碰点放在虚拟手的各个手指的指尖处，通过点接触来计算物体间相互作用力。

虚拟场景中3 个物块分别具有软、硬、脆不同材质属性。 通过弹簧-质子模型算法和柔性物体反馈算法模拟出刚性、脆性、软性物体的材质质感的力学模型，使得操作者可以通过手控器触摸时感受到不同材质的区别。 如果抓握软的和脆的物块时力过大，会导致物块形变或破碎，物块一旦形变程度过大会逐渐变成红色，破碎则直接变为红色，但依然能够继续进行操作。 在开启力反馈后，抓握的过程中会感受到持续的反馈力感。

本试验的任务是在随机指定的区域内通过操纵虚拟手夹取3 个物块，并把物块按一定顺序拼到一起，以模拟机械臂拼接物体任务。 在夹住物块的过程中不能将物块损坏，也不能在拼接过程中将其他物体损坏。

试验选取10 名受试者(5 男5 女)参加，试验前受试者允许提前熟悉系统的操作。 试验时，受试者随机编号，并按编号顺序依次进行试验。 每位受试者分别进行2 组操作：无力反馈操作和开启力反馈操作。 受试者每组操作需完成3 次，记录每次操作的完成时间和损坏情况，取3 组完成时间的平均值作为该组操作的完成时间，3 组损坏次数的平均值作为该组操作的损坏次数。 具体如图12 所示。

图12 虚拟夹取实物操作实例Fig.12 Example of virtual clamping operation

试验结果如图13、14 所示，从整体上看，操作者对3 种材质的物块可明显感受到不同的力觉反馈，能够帮助操作者对抓握力度进行调整。 有力反馈的试验均比无力反馈的试验完成的时间要快，并且仅有一次出现损坏虚拟物体的情况，而无力反馈损坏次数较多。 有力反馈的试验平均完成时长为9.45 s，最长耗时12.1 s，最短耗时8.2 s，平均损坏次数0.1 次，损坏概率为10%；无力反馈的试验平均完成时长12.39 s，最长耗时16.2 s，最短耗时10.8 s，平均损坏次数0.8 次，损坏概率为60%。 试验结果表明，有力反馈的试验比无力反馈的试验平均完成时间缩短了23%，损坏率降低了50%，大幅提高了抓取操作任务的准确性和安全性。

图13 完成时间试验结果Fig.13 Results of completion time in the experiment

图14 损坏情况试验结果Fig.14 Results of damage in the experiment

7 结论

本文构建了一套面向空间站机械臂遥操作的虚拟人机交互系统。

1)其中力反馈手控器通过混联式设计，实现了三维平动自由度和三维转动自由度的机械解耦，并通过标定修正了存在误差的机械参数，提高了位置精度。 通过对手控器进行了静力学分析，解耦结构降低了力与力矩解算的复杂度。

2)控制系统搭建位置-速度-电流串级PID算法实现了对输出电流、运动速度、末端位置的闭环控制，实现了对末端输出反馈力的稳定控制。

3)试验验证了人机交互系统可以为操作者提供250 mm×250 mm×250 mm 的工作空间和大于15 N 的反馈力，末端三维位置精度可达0.6 mm。 相较于无力反馈的系统，操作者平均完成时间缩短了23%，损坏率降低了50%，可以更加快速、准确、安全地完成抓取操作任务，提升了操作效率和系统的安全性。