可适应多维度信息变化的智能星图识别方法

李 冰 高晓颖 踪 华 李林浩

1.宇航智能控制技术国家级重点实验室，北京100854； 2.北京航天自动控制研究所，北京 100854； 3.北京理工大学，北京 100081

0 引言

天文导航是基于天体已知的坐标位置和运动规律，应用观测天体的天文坐标值来确定航行体的空间位置等导航参数。天文导航属于完全自主式的导航方式，不受时域、地域和空域的限制，适用范围广，无需路基台站的辅助，设备简单，不受人为或自然形成的电磁场干扰，不向外辐射能量；具有隐蔽性好，工作稳定，定位、定向精度高，无累积误差等优点[1]。随着星敏感器等新型敏感器的出现，天文导航在航天器上也有着较大的发展空间，如何利用星敏感器得到的信息来定轨定姿，从而进行姿轨控制，已经成为当前研究的热点，而星图识别作为姿态解算的前提，也成为重要的研究课题[2]。

常用的星图识别算法主要分为2大类：1)角距匹配识别法，包括最为典型的三角形算法和各种改进的三角形算法[3-9]。2)模式识别法，比较典型的算法为Grid算法[10-12]。

这些传统的算法虽已基本满足工程应用，但当星敏感器角距误差和星等误差增大时，存在鲁棒性较差的缺点。主要表现在这些算法在匹配时，需要预先设置一个匹配门限。在线应用中，当星敏感器星角距测量误差增大后，则受嵌入式信息处理机存储空间的影响和软件安全性考虑，不可随意增大匹配门限，因此，无法完成星图识别。同时由于星敏感器对星等的测量不是十分准确，星图识别方法需要降低对星等误差的敏感度。

针对以上传统星图识别方法的不足，本文提出了一种利用星点角距信息和星等信息的卷积神经网络识别方法。同时为了扩大样本的覆盖性获得更好的网络训练效果，提出了一种变视场主轴，基于星角距信息和星等信息的星样本集生成方法，另外随机加入星等误差和角距误差，得到了覆盖性高的网络样本集合；然后设计卷积神经网络模型；最后利用训练样本对网络进行训练，并对训练好的网络测试验证。

本文针对由于星敏感器星等测量的不准确性导致的星等变化和由于视场主轴变化导致的星点变化，设计神经网络架构且能够适应以上多维度信息变化。在线应用时，只需要存储导航星信息星表，因此，星表容量小，且对星角距误差和星等误差的鲁棒性好。

1 训练样本构建方法

训练样本构建思路为：为了便于网络实现星图分类，规定了同一类星图的定义方法，提出了通过改变视场轴指向获得星集的方法；提出了具体的样本数据计算方法，即对每一星集，利用其它星到主星的角距和星等信息构建样本数据，增加星等误差、角距误差对样本扩充，获得覆盖性比较全的样本数据。

1.1 星集类定义及构建方法

考虑到星敏感器拍摄星图的实际情况，将视场轴对准某一恒星，将绕该恒星作一定角度变化条件下拍摄的所有星图均规定为同一类。具体方法为：

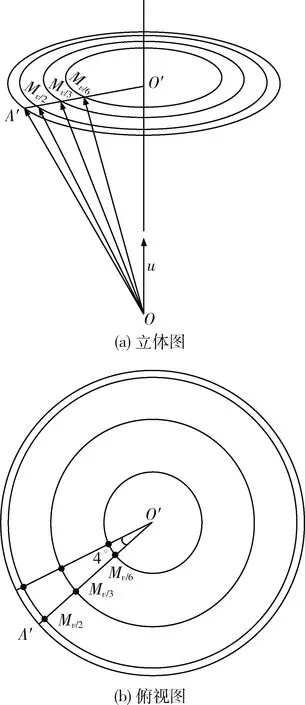
图1 变视场主轴方法示意图

1.2 样本数据构建方法

根据1.1节的定义，按照视场轴向、星集和角距等计算可以获得样本数据，主要的计算方法如下所述。

1.2.1 变视场主轴计算方法

当视场主轴对准某一颗星点时，则视场主轴方向与该星点在天球坐标系下的矢量方向重合。当视场主轴围绕该星点进行变化时，则需要重新计算视场主轴在天球坐标系下的矢量方向。

如图2所示，视场角为υ°，视场主轴对准星点O′，其坐标为(α,β)。视场圆与天球面相交于A点，则A点坐标为(α,β-υ)，那么当视场主轴方向指向A点时，其矢量方向与A点重合。当视场主轴指向方向改变为圆O′上的点时，则需要重新计算视场主轴的矢量方向。

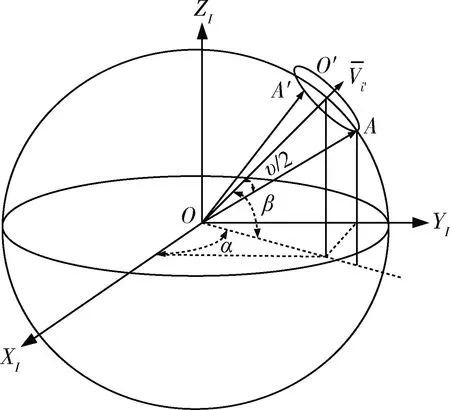
图2 视场主轴对准星点时的情况

如图3所示，视场主轴方向沿圆O′变化问题可以等效为刚体相对坐标系做定点转动问题，详细原理与推导见文献[13]。

将天球球心与视场面组成的三角锥提取出来，记u为OO′的单位矢量，r=OA，r′=OA′，现问题转化为求解r′，如图3所示。

则可以推得，

r′=rcosθ+(1-cosθ)[r+u×(u×r)]+

u×rsinθ=r+u×rsinθ+(1-cosθ)u×

(u×r)

(1)

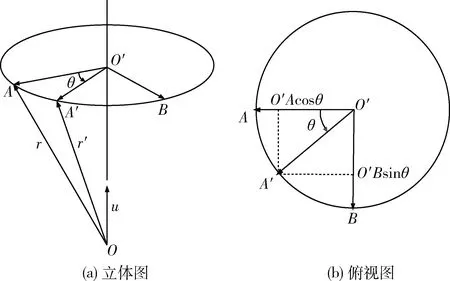
图3 刚体的等效旋转示意图

因此，给定任一角度θ，即可求得矢量r′，进而得到A′在天球坐标系下的赤经、赤纬。

1.2.2 星图样本计算

对每一个视场轴指向，利用文献[14]中的方法，计算视场内的导航星集。然后计算其它星距离主星的角距，由角距和星等信息构成训练样本。角距计算方法为：

如图4所示，恒星在天球球面坐标的赤经和赤纬记作(α,β)。根据直角坐标与球面坐标的关系，可以得到每颗恒星在天球直角坐标系下的方向矢量为

(2)

而星角距可以直接根据构成星对的2颗导航星i和j在导航星表中的方向矢量计算得到，即

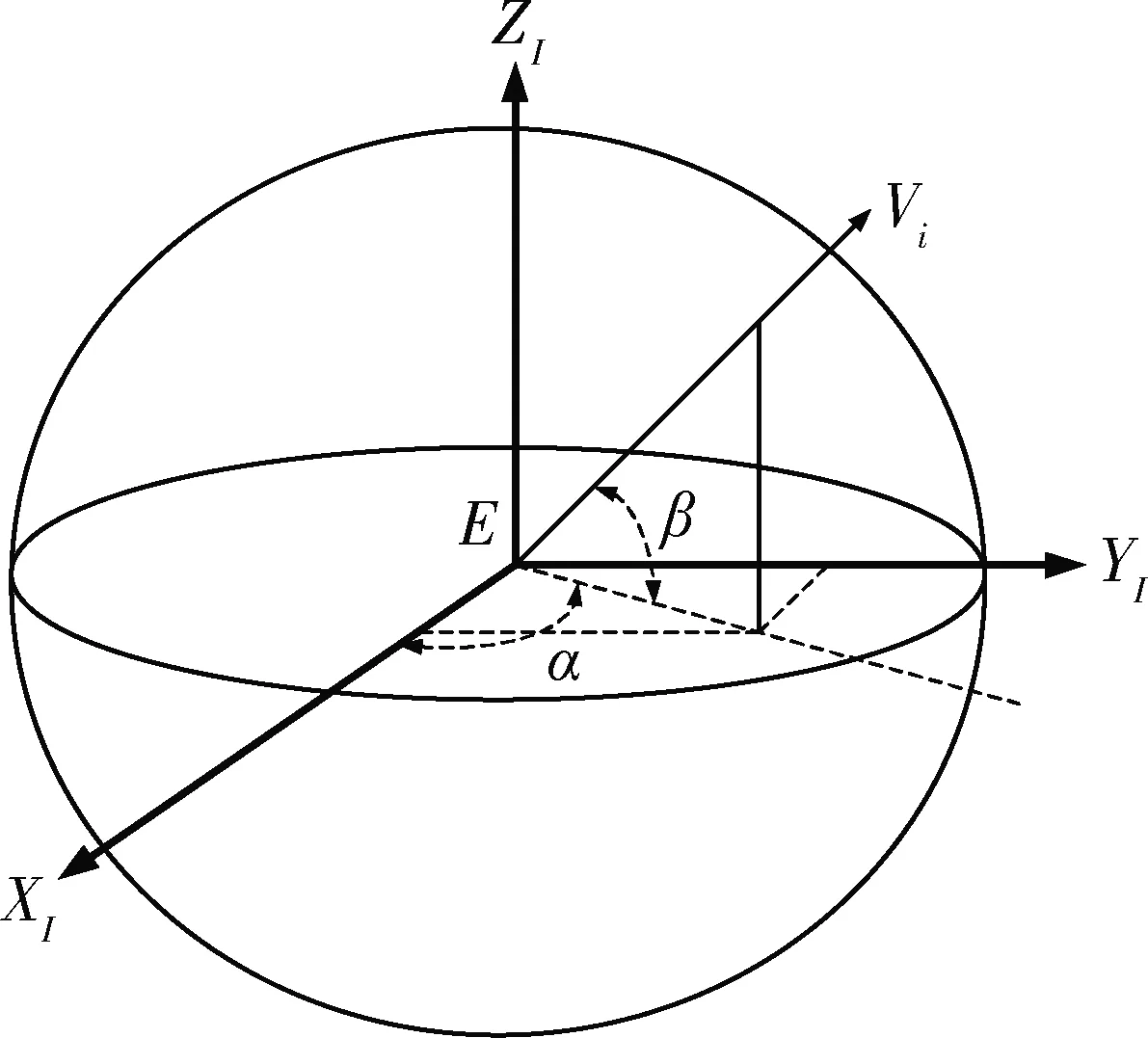
图4 地心惯性坐标系定义

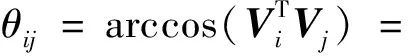
arccos(VixVjx+ViyVjy+VizVjx)

(3)

其中，Vi和Vj为两导航星在星表中方向的矢量形式。

1.2.3 星图样本扩充方法

分别生成训练集与测试集样本，其中训练集与测试集样本比例为2∶1，均按照如下方法生成：

为了提高神经网络的适应性，对1.2.2中的每个样本数据增加星角距误差和星等误差，进行样本扩充。

1)对每种情况的样本加入星等误差，认为在6等星以内的星点为可见点。由于星敏感器对于星等的测量准确度不是很高，因此需要考虑星等测量误差导致的星图变化。首先，获得每种情况下可见星点的星等，对每个点加入星等误差，当加入误差后的该点星等仍在6以内的，视为可见。由于星等越小，星点越亮，所占的权重应该越大，因此考虑将其进行取倒数处理，即

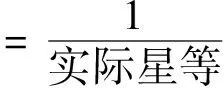
(4)

2)对每种加了星等误差的星点情况，加入随机角距误差。

3)分别将加了误差的星等信息和角距信息储存下来。为保证不同星图储存的信息尺寸一致，当角距信息不足时，其余列补0，如表1所示。

表1 星图角距信息储存矩阵示例

其中，d1,j(j=2,3,…)为视场内主星到伴星之间的角距，1表示主星；Mj(j=2,3,…)为对应角距信息的伴星星等的倒数(伪星等)。

2 卷积神经网络构建

为了充分利用星角距信息和星等信息，并降低星等误差的影响，构建了一种卷积神经网络。在卷积层，利用1×1的卷积核实现对角距和星等信息的加权处理。通过网络训练，实现星等大的权重低的设计初衷，从而增强对星等误差的鲁棒性。

如图5所示，卷积神经网络共有5个卷积层，3个全连接层。卷积层卷积核均为1×1。本文的神经网络输入信息为2维(角距信息和星等信息)，因此将输入端的通道数设置为2。因为只对不同通道的数据进行融合，所以第1层卷积核的大小设置为1×1×2×32，32为第1层卷积的输出通道数。在进行多次卷积之后，再使用全连接层对卷积得到的信息进行综合处理。

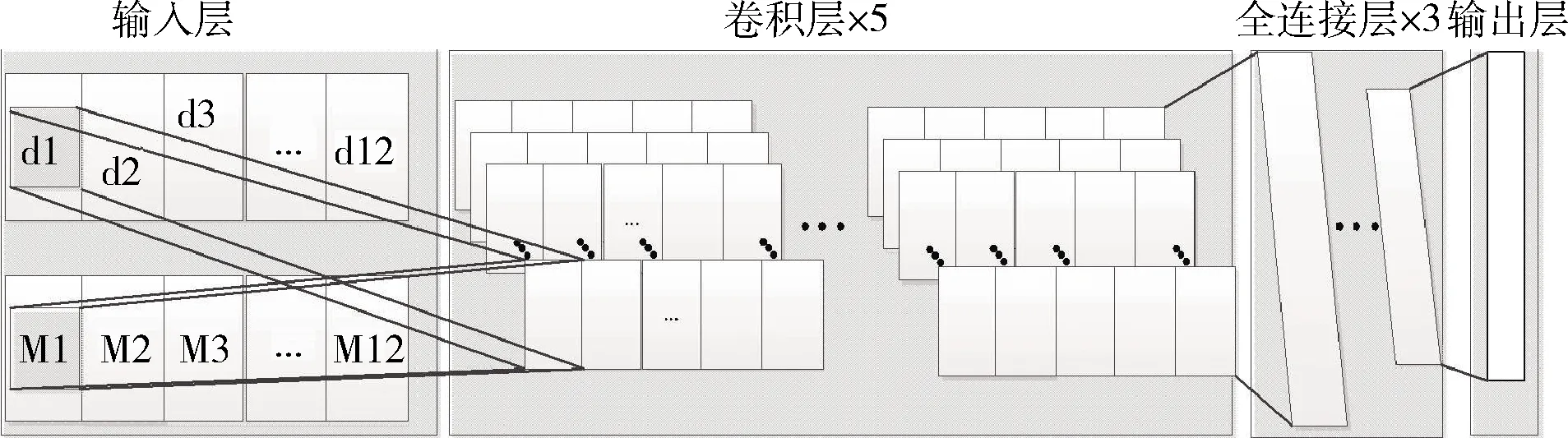
图5 神经网络结构示意图

本文将识别问题认为是一个分类问题，因此使用cross entropy作为损失函数。

3 仿真校验

神经网络模型基于tensorflow平台搭建，使用Python语言来实现。

对北极天区进行仿真验证，视场大小为8°×8°，通过变视场主轴的方法得到107类，视场内星点数目最多为12颗。

为了验证本文卷积神经网络设计的有效性，在考虑不同角距误差和星等误差的条件下，进行了测试验证，并与全连接神经网络进行了对比分析。

仿真1：全连接神经网络与卷积神经网络对星图角距误差的鲁棒性探究。

首先生成不添加星等误差、仅含角距误差为±0.06°的训练样本，然后分别构建全连接神经网络和单通道卷积神经网络。卷积神经网络共有8层，使用ReLu非线性激活函数和cross entropy损失函数。使用相同的数据训练1000步直至网络收敛。

然后再使用相同的测试数据对网络进行测试验证，结果如表2所示。

从表2可以看出，随着角距误差的减小，两种网络的识别率逐渐增大，同时卷积神经网络的识别率普遍高于全连接网络的识别率，尤其是样本角距误差增大时，更为明显。

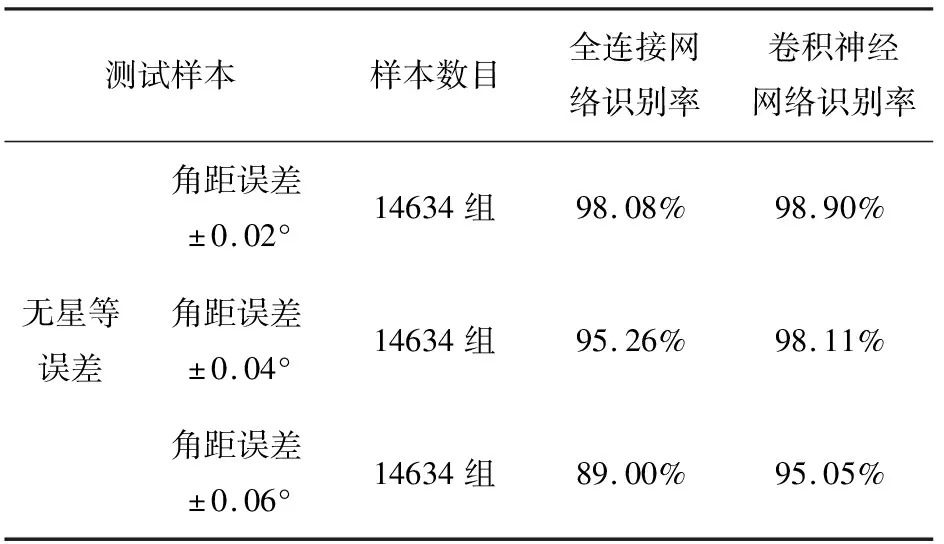
表2 无星等误差时不同网络的识别情况

分析原因，由于使用变视场主轴的样本生成方法，因此同一类别下，可能会出现不同的星点情况，导致角距信息数据不一致，全连接神经网络针对数据不一致的同类情况鲁棒性不是非常高，而卷积神经网络鲁棒性更好一些，因此识别率更高。

仿真2：全连接神经网络与卷积神经网络对星角距和星等误差的鲁棒性研究。

首先对每类情况下的星点随机加入范围为±0.2MV的星等误差，然后再随机加入角距误差，误差范围为±0.06°。将星等信息和角距信息储存下来。使用相同的数据，分别对全连接网络和卷积神经网络进行训练并保存模型。全连接神经网络的输入仅为角距信息，卷积神经网络为星等和角距两通道信息。训练结果如图6～7所示：

图6 卷积神经网络训练准确率随迭代次数变化图

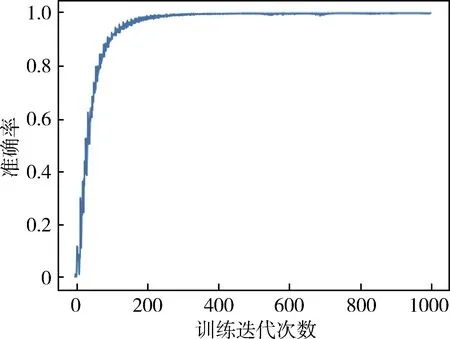
图7 全连接神经网络训练准确率随迭代次数变化图

从图6～7可以看出，训练时的准确率在训练一定步长后收敛，同时保持在一个较为稳定的范围内，说明模型具备了可以用来测试的条件。

然后生成±0.2MV的星等误差测试样本和角距误差测试样本，角距数据误差范围分别为±0.02°、±0.04°和±0.06°。

将以上测试样本放入已经保存的神经网络模型中进行测试，测试时识别率如表3所示：

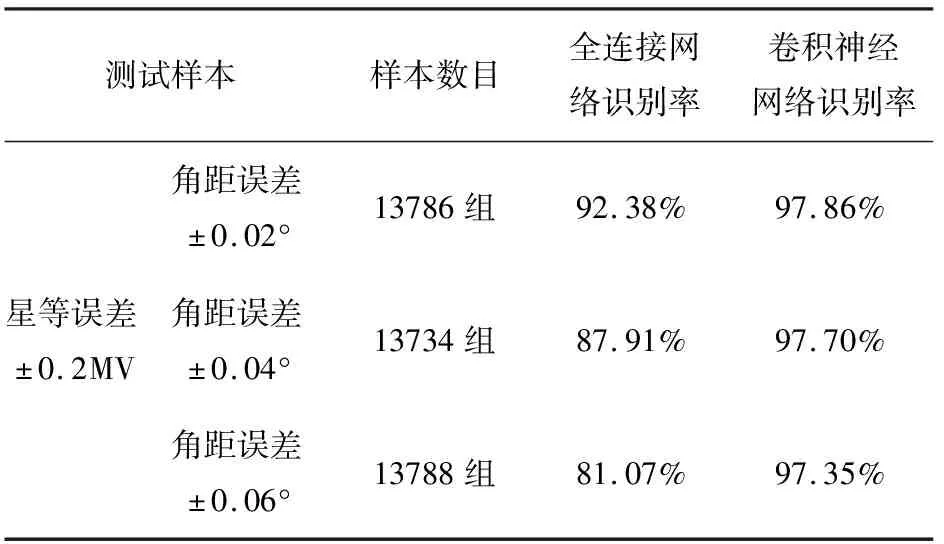
表3 测试样本识别率

测试样本与训练样本是分开生成的，且测试样本中的误差均为随机加入。测试样本数量较大，充分模拟了该种误差下可能出现的情况。

从表3可以看出，测试时，分类精度较高，最低时为97.35%。仿真结果表明该神经网络结构和参数能很好地融合多维度信息，同时星等信息的加入能够提升网络的识别率。在加入了星等误差后，卷积神经网络的识别率明显比全连接网络的识别率高，表明卷积神经网络对于变视场主轴导致的同类别下数据维度不一致有着较好的鲁棒性。

4 结论

本文所提出的基于卷积神经网络的星图识别方法相比于传统的角距匹配法更简单，在实际使用时充分利用了星图信息，不需要多次搜索星表。由于网络参数自动更新，充分融合了多维度信息，降低了计算量，提高了匹配效率。通过变视场主轴的星图生成方法，扩大了样本覆盖性，提升了识别可靠性。本方法不仅能够适应视场主轴变化带来的星图变化，还能够适应星等误差导致的星图信息变化。在星等误差为0.2MV时，本方法仍能保持97%以上的识别率，对星敏感器的星等误差有着较高的鲁棒性。本方法对角距误差有更高的鲁棒性，对于一般的基于角距匹配的算法，角距误差通常在±0.02°左右，本方法将角距误差提升至±0.04°和±0.06°时，仍然能够保持很高的识别率。在飞行器飞行环境复杂、星敏感器测量误差大的条件下，本方法具有更大的应用优势。