带对数非线性项的(p,q)-Laplacian型方程的多解性

林荣瑞 高云龙

（六盘水师范学院数学与计算机科学学院，贵州六盘水553001）

近年来，偏微分方程引起了许多数学工作者的兴趣。椭圆型方程作为偏微分方程领域的一个重要分支，在许多实际应用诸如力学、气候学、冰川学等问题中经常遇到，其中对p-Laplacian 方程的研究，受到很多学者的广泛关注，出现了很多这方面的文献，如文献［1-5]等。关于（p,q）-Laplacian型方程也受到了许多学者的研究，如文献［6-9]等。但以上学者都是对带有对数非线性项的偏微分方程进行研究，目前还没有对带有对数项的（p,q）-Laplacian 型方程的研究。本文将研究以下带变号对数非线性项的（p,q）-Laplacian型方程

其中Ω 为RN中的光滑有界区域，

1 预备知识

下面将给出后文所需要的定义和引理，然后构造问题（1）对应的变分结构，将寻求问题（1）的非平凡解转化为寻求其对应变分泛函的临界点.

定义1.1在假设下，由

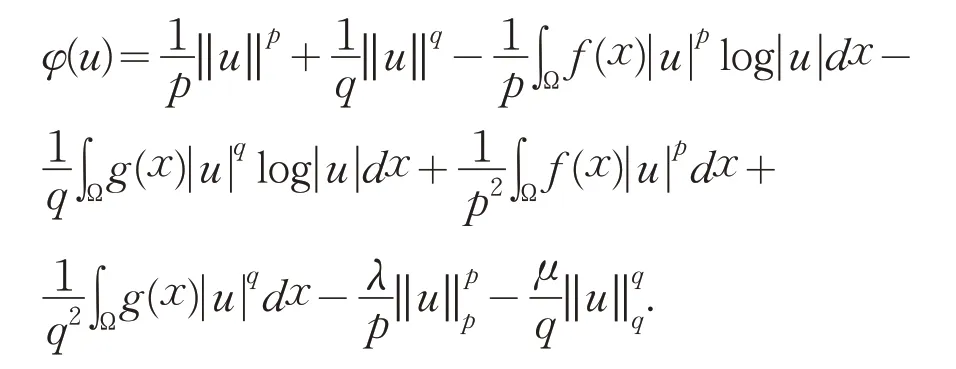
此外，φ的临界点是问题（1）的经典解.以下假设λ,μ满足式（26）.

引理1.1（对 数Sobelev 不等式）［10]2076-2091设p,q>1,δ,ζ>0 且u∈W1,p(ℝN){0}，则

其中

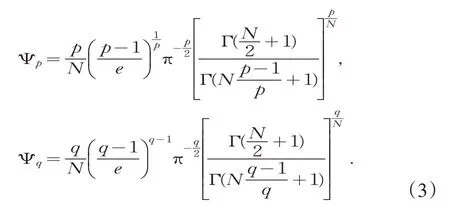
如果u∈W1,p(ℝN){0}，令u(x)=0,x∈RNΩ，则

引理1.2设且满足

∫Ωf则

证明由可以得到

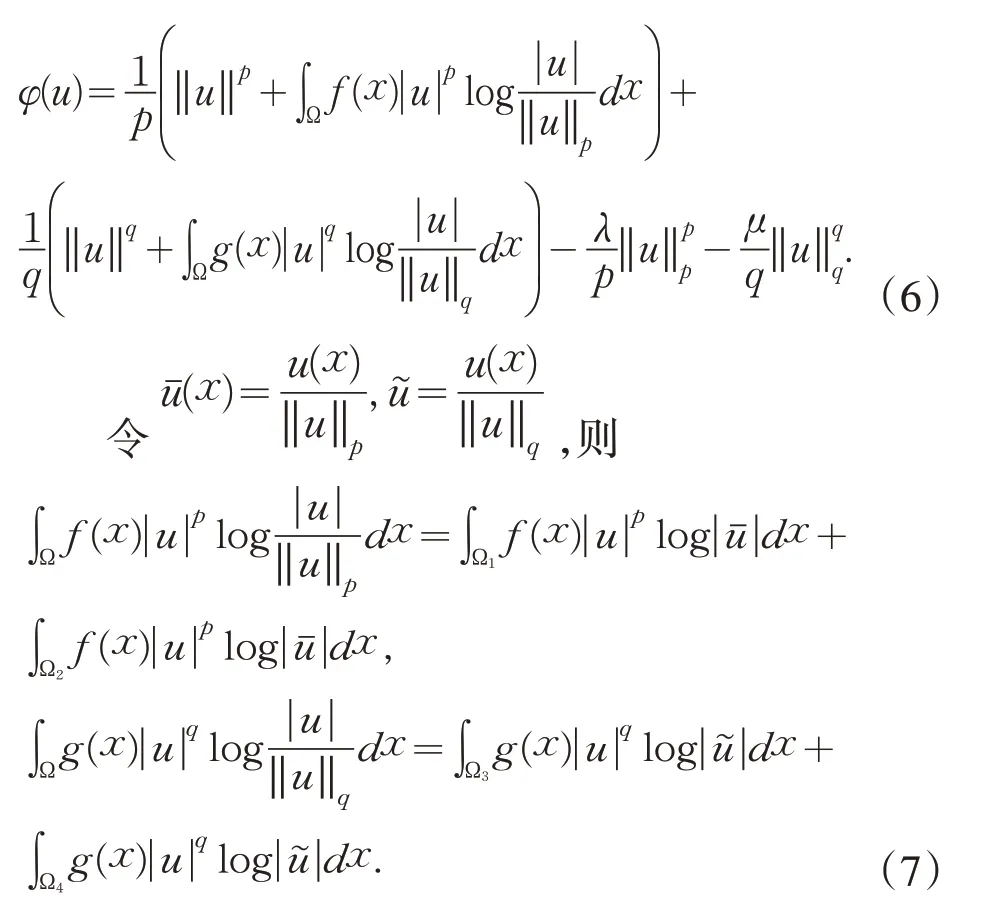
式中:

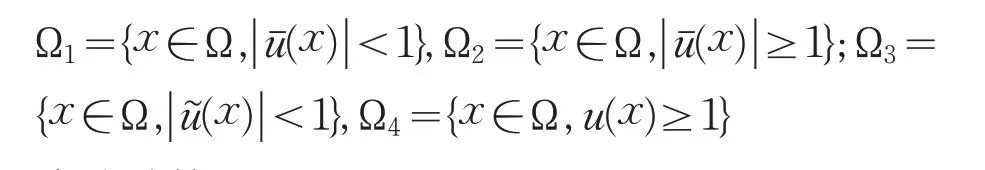
直接计算可得

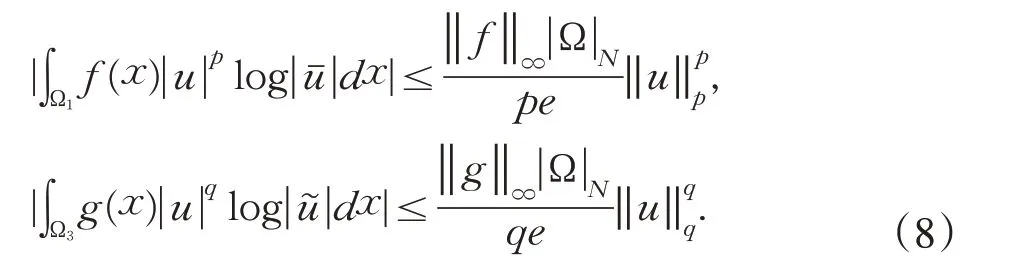
由对数Sobelev不等式（3）和式（8）可得

将式（7）∼（9）代入（6）可得

即可得到式（5）.

2 解的多重性

这一节，将在Nehari流形上研究问题（1）的弱解.显然，φ在上下方无界，但在Nehari流形ℕ上是下方有界的 ，其中，显然，φ的非平凡临界点一定在ℕ 上.由式（5）可以推得

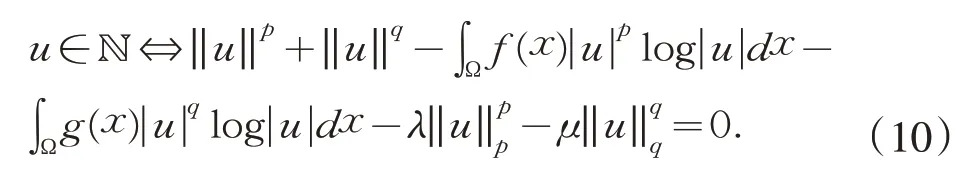
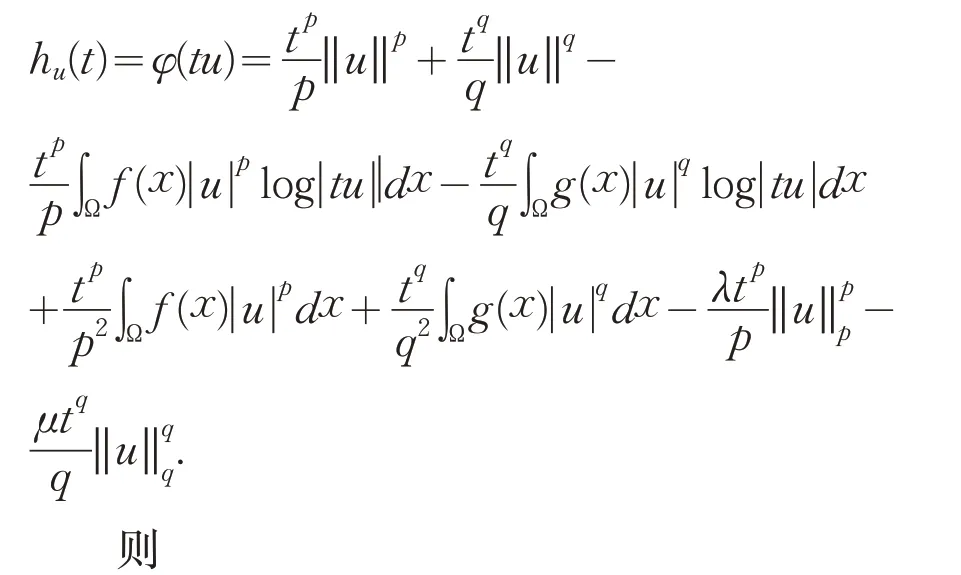
引理2.1设且t>0，则tu∈ℕ 当且仅当

证明根据式（10）和式（11）及t>0 ，可得tu∈ℕ 当且仅当若u∈ℕ ，则

因此，我们将ℕ 分成三部分：ℕ+,ℕ-和ℕ0,其中

引理2.2若u0是φ在ℕ 上的一个局部极小元且u0∉ℕ0,则φ′(u0)=0.

证明设u0是φ在ℕ 上的一个局部极小元，则由拉格朗日乘数法知，存在ε∈ℝ 满足其中

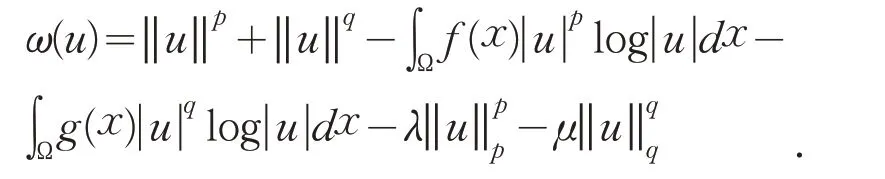
因为u0∈ℕ ，所以另外，由于u0∉ℕ0，因此

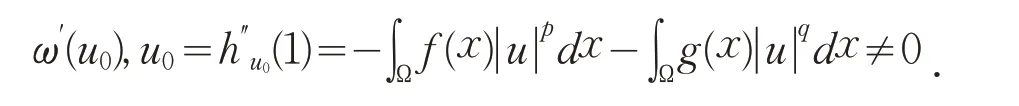
故ε=0，进而

引理2.3ℕ+,ℕ-均非空，且ℕ+是有界的.

证明由文献［6]的引理5，令p=q即可得ℕ+,ℕ-均非空.下证ℕ+是有界的，假设ℕ+是无界的，则存在使 得当n→∞时，令则不失一般性，设存在一个使得在空间中满 足υn⇀υ0，在 空 间Lp(Ω) 中υn→υ0成 立.由

所以

又由u∈ℕ 和式（10）知

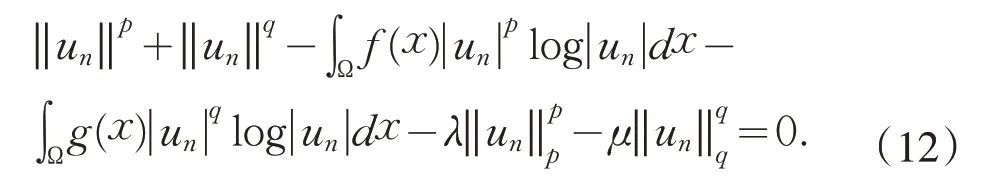
直接计算可得

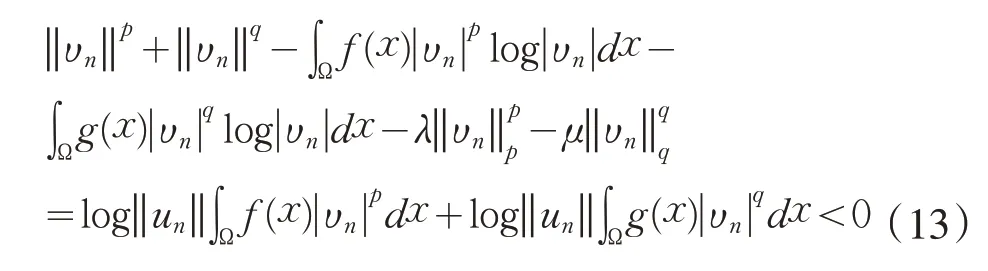
类似式（7）∼（9），再结合‖υn‖=1 可以得到

其中C与n无关. 再有式（13）∼（14）及可得

另一方面，由υn⇀υ0但υn→υ0，可推导存在的子列，仍记作使得

再结合式（13）和式（15）有

另一方面，由υn→υ0，存在{υn}的子列，仍记作使得式（16）和式（18）成立，且有

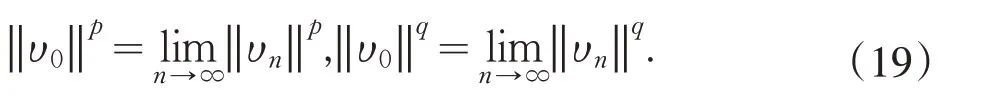
再结合式（13）和式（15）有

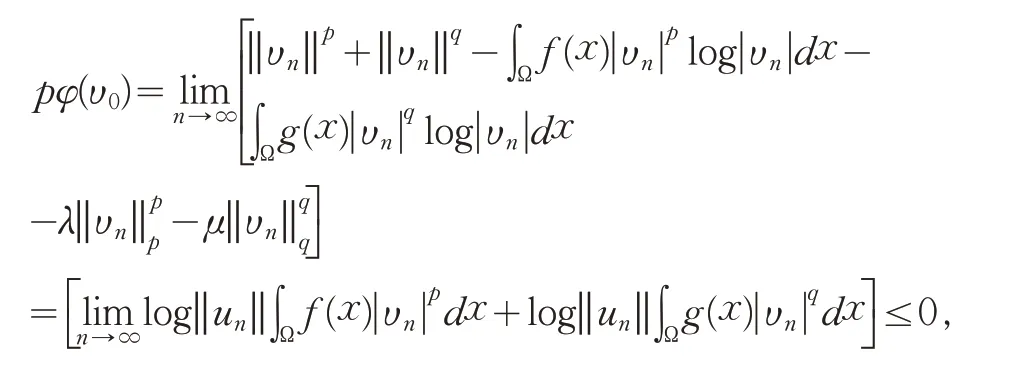
矛盾.因此，ℕ+是有界的.

引理2.4(1)φ在ℕ+上下方有界；(2)φ在ℕ+上有极小元.

证明(1)因为u∈ℕ+，所以由式（10）可得

理2.3可得，ℕ+是有界的，故φ在ℕ+上下方有界.

(2)设{ }un是φ在ℕ+上的一个极小化序列，即由引理2.3 知是有界的.不失一般性，设存在u0∈W1,p

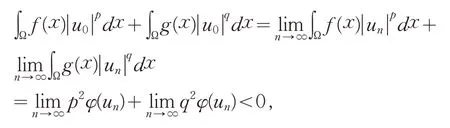
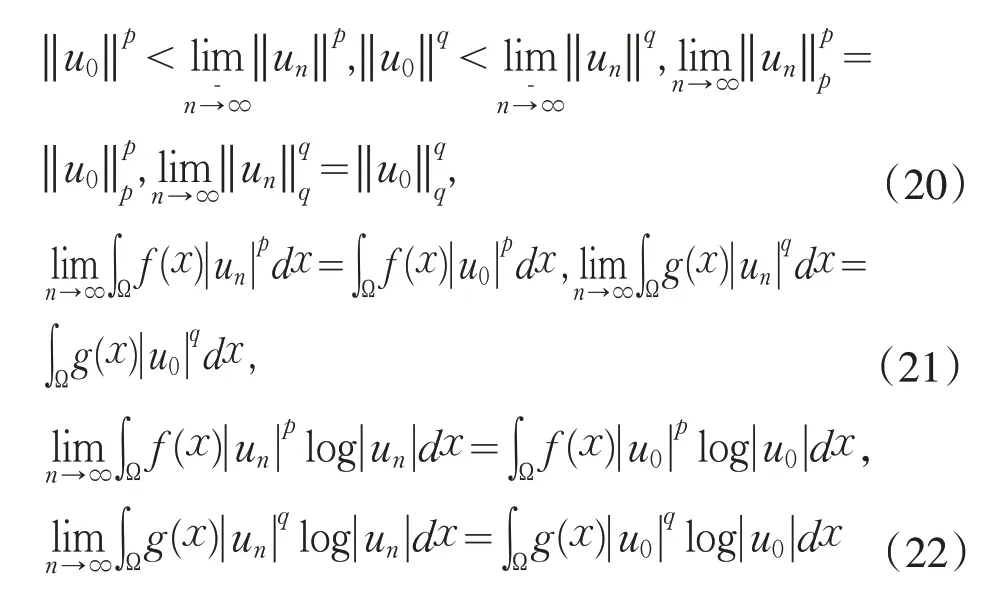
成立,再结合式（12）有

因此，存在

使得t(u0)u0∈ℕ+，则hu0在t(u0)处取得极小值，再结合式（20）∼（22）有

引理2.5φ在ℕ-上的一个极小化序列都是有界的.

证明设是φ在ℕ-上的一个极小化序列，即

假设un是无界的，不妨设令有界.不失一般性，设存在一个使 得 在 空 间中 满 足υn⇀υ0在空间Lp(Ω)中υn→υ0成立.由un∈ℕ 知,式（12）成立.直接计算可得式（13）和

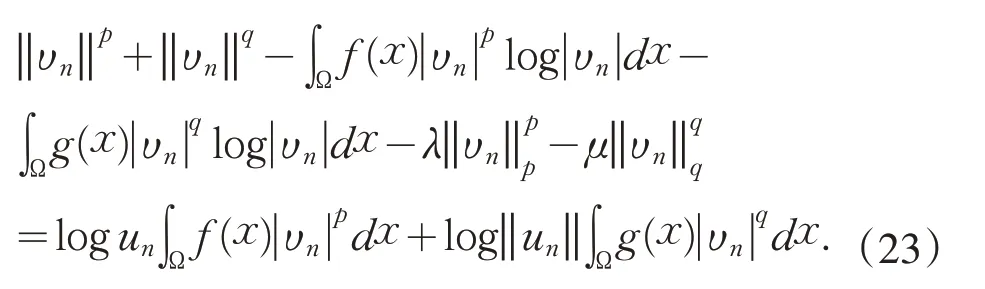
另一方面，由υn⇀υ0但υn→υ0可推导存在子列，仍记作使得式（16）∼（18）成立，再结合式（15）和式（23）有

矛盾.

另一方面，由υn→υ0知,存在的子列，仍记作使得式（16）∼（19）成立，再结合式（15）和式（23）有

矛盾.因此，φ在ℕ-上的一个极小化序列都是有界的.

引理2.6在ℕ-上存在极小元.

证明(1)假设设是φ在ℕ-上的一个极小化序列，即

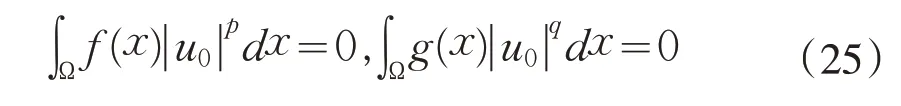
另一方面，由un⇀u0且un→u0可得存在的子列，仍记作使得（20）∼（22）成立.再结合式（12）和（25）有

-λ矛盾.若在空间中有un→u0，则由式（5）和注解1得

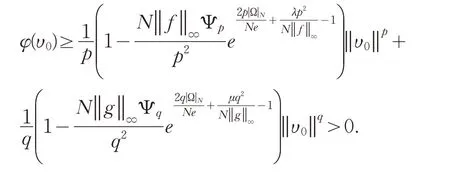
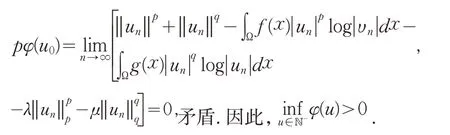
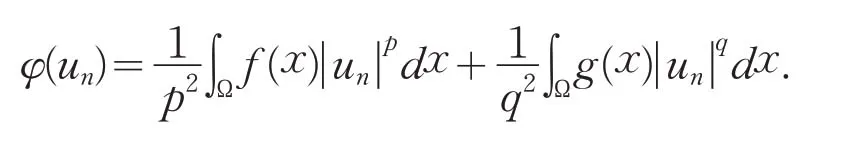
再由（1）有

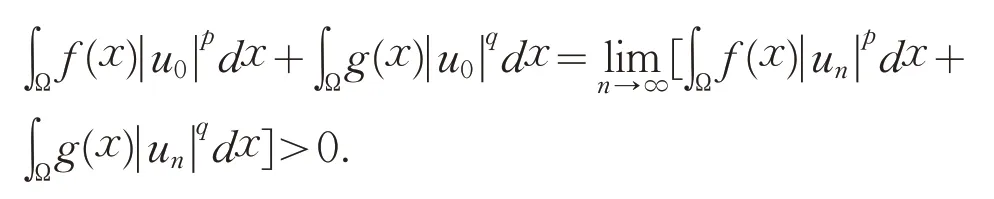
因此，存在t(u0)使得t(u0)u0∈ℕ-，由于在中t(u0)un⇀t(u0)u0，但t(u0)un→t(u0)u0，则存在{t(u0)un}的子列，仍记作{t(u0)un}，使得

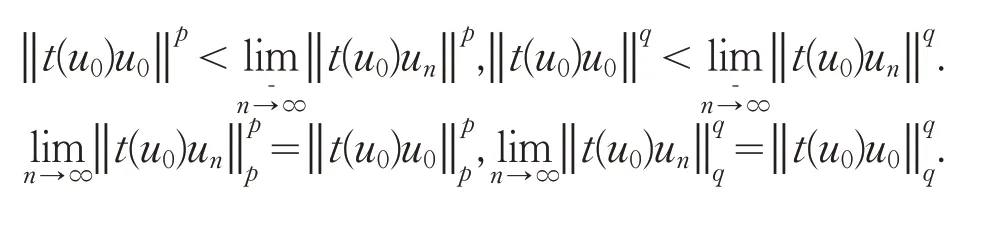
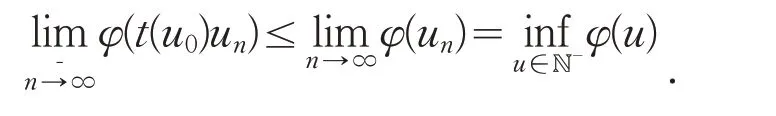
定理2.1设且在上是变号的，λ,μ>0 满足

则问题（1）至少有两个非平凡解，其中|Ω|N为Ω 在RN中的测度，Ψp,Ψq将由式（3）定义.

证明由引理2.4(2)，引理2.6(2)表明泛函φ有两个极小元u+∈ℕ+和u-∈ℕ-.再由引理2.2知，u+和u-是问题（1）的两个非平凡解.