多参数n阶α次积分半群的预解集

2020-07-01毕伟

延安大学学报（自然科学版） 2020年2期

毕伟

(延安大学学术期刊中心，陕西延安 716000)

在算子半群理论中，预解集是各类算子半群研究的重要内容。2014年，张明翠等[1,2]提出了单参数n阶α次积分C半群的定义并研究其相关性质；赵丹丹等[3,4]给出了双参数n阶α次积分C半群的概念及其预解集的性质。根据上述文献，本文给出多参数n阶α次积分半群的预解集的定义，并研究其预解式的一些性质。

1 预备知识

在本文中，N表示自然数集，X为无限维的复Banach空间，B(X)是X上有界线性算子全体所成的Banach代数，D(A)为线性算子A的定义域，在全文中规定所有n∈N，m∈N,α≥0。

JnT(t)表示T∈C(「0,+∞),X)的n次积分，即

T=0当且仅当存在n>0使得

JnT(t)=0,t≥0。

定义1[5]设n∈N，α≥0，{T(t1,t2,…,tm)}t1,t2,…tm≥0⊂B(X)强连续，若存在线性算子A=(A1,A2,…,Am)使得(1)～(3)式成立：

(1)∀x∈X,t1,t2,…,tm≥0，

JnT(t1,t2,…,tm)x∈D(A)，

AJnT(t1,t2,…,tm)x；

(2)∀x∈D(A),t1,t2,…,tm≥0，

JnT(t1,t2,…,tm)Ax；

(3)T(t1,t2,…,tm)=

T(t1,0,…,0)T(0,t2,…,0)…T(0，0，…，tm)。

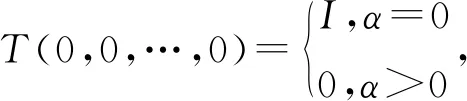
当α=0时，{T(t1,t2,…,tm)}t1,t2,…,tm≥0称为多参数n阶强连续算子半群。

2 主要结果

定义2 若R(λ,(A1,A2,…,Am))=λn-1(λn-(A1,A2,…,Am))-1有定义在Banach空间X上的有界逆算子，则称λ为多参数n阶α次积分半群{T(t1,t2,…,tm)}t1,t2,…,tm≥0的次生成元A=(A1,A2,…,Am)的正则点，R(λ,(A1,A2,…,Am))为A=(A1,A2,…,Am)的预解式，全体正则点称为A=(A1,A2,…,Am)的预解集，记为

定理1 设n∈N,α≥0,{T(t1,t2,…,tm)}t1,t2,…,tm≥0为X上的多参数n阶α次积分半群，闭线性算子A=(A1,A2,…，Am)为其次生成元，且D(A)⊂X，如果有

{λn|Reλ>max{ω,0}}⊂

∀(a1,a2，…,am)∈Rm，ω∈R，那么下式成立：

R(λ,(A1,A2,…,Am))x=

∀x∈X,t≥0。

证明A=(A1,A2,…,Am)是X上的多参数n阶α次积分半群的次生成元，且Reλ>max{ω,0},x∈X，则有

并且

对于固定转速离心压缩机（简称压缩机）流量、压力关系见图1。当流量降至Q1，操作点移至S1，压缩机发生喘振工况，叶轮和扩散器开始出现倒流，出口压力降低，噪音和振动发生，压缩机失去维持稳定操作的能力。严重的喘振可能导致压缩机机械密封、轴承及叶轮的损坏，造成不可挽回的经济损失。对于离心式压缩机，启动、停车、以及入口介质的压力、温度、比热、摩尔质量和压缩系数等任何参数发生变化，都可能使压缩机操作点到达S1，引起压缩机的喘振。在喘振系统设计时，通常通过设定喘振控制点S2（图1）和喘振实际发生点之间的安全余量来为喘振调节系统提供反应、调节时间。

那么由∀(a1,a2,…,am)∈Rm，令