三体对抗策略的预警机主动防御最优协同制导算法

王小平， 周 问， 刘 博

(空军工程大学航空工程学院， 西安， 710038)

主动防御[1]本质上属于飞机规避导弹技术中的一类，但是与传统飞机规避导弹技术不同，主动防御采用直接、主动型的进攻防御方式代替了传统被动、防守型的逃逸方式，直接发射防御空空导弹对来袭攻击导弹实施拦截，将传统上的近身逃逸变成了远程防御，从而使飞机不必放弃原有的攻击态势以及飞行任务，大大提高了飞机的安全距离，牢牢把握了战场的主动权。

相比其他规避策略，主动防御策略的产生相对较晚。从2010年以来，对主动防御技术的研究才正式步入正轨。Ilan Rusnak[2]引入飞机、防御导弹、攻击导弹的加速度限制，将主动防御问题转化为动态博弈问题，采用脉冲函数法得到了防御导弹的次优主动防御导引律。文献[3～5]建立了主动防御飞机、防御导弹、攻击导弹的对抗模型，将主动防御问题转化追踪逃逸问题，采用终端投影的方法实现了模型的降阶。文献[6]分析了防御导弹与攻击导弹采用不同导引律时的对抗结果，推导出了不同条件下防御导弹的发射包线和指令加速度。

当前复杂空战中，以比例导引律为代表的传统制导律对于高速机动飞行器的精准拦截要求已经无法满足[7]。为了满足的作战条件日益复杂的要求，学者们应用现代控制、非线性控制等方法提出了自适应控制制导律、微分对策制导律、滑模控制制导律，最优控制等多种制导律。花文华等人采用自适应滑模控制的方法，对主动防御导引律进行了设计[8]；Song Junhong等人针对多枚导弹协同拦截机动目标的三维末制导问题，利用自适应和非奇异快速终端滑模理论，提出了一种新的具有冲击角约束的有限时间协同制导律[9]；Chen Jian等人针对追逃问题中的高超声速目标，提出了一种基于非线性比例和微分制导律(NPDG)的分数演算制导算法，有效地减小了针对目标机动的误击距离，提高了抗干扰能力和鲁棒性[10]。

在研究能量消耗时，Yamasaki[11]基于最优控制理论，通过在性能指标函数中加入防御导弹的控制能量，提出了改进视线角指令制导律；当防御导弹和目标飞机的转弯率存在约束时，Garcia[12]在最优控制理论下目标机的最优航向角进行了研究，使得防御导弹拦截攻击导弹时，目标机能够将其引诱至防御导弹附近。Martin Weiss[13-14]等人针对主动防御对抗系统，以拦截导弹与攻击导弹的脱靶量最小，并且总控制能量最小为优化目标，设计了最优制导律。Rusnk[15]将3种飞行器的控制能量、目标机的脱靶量和防御导弹的脱靶量加权求和得到了性能指标，其结果显示如果后者的权重系数趋于零时，将能够简化目标机和防御导弹的最优对策制导律。Rubinsky[16]在考虑到过载受限的情况下，提出了攻击导弹远离防御导弹并持续靠近目标机的最优微分对策。

以上这些研究都是在二维平面进行的验证性研究，但是在实际的主动防御过程中，整个作战过程是在三维空间中完成的，因此二维平面内进行的简化研究难以直接应用于实战中，如何在现有主动防御制导律的基础上实现在三维空间下防御导弹对攻击导弹的成功捕获，是目前面临的一个亟待解决的问题。

1 攻击导弹-目标机相对运动方程

假设攻击导弹攻击目标机发生在末制导段，且防御导弹、攻击导弹滚转角为0°。图1为二维下攻击导弹、目标机的相对运动学关系，将攻击导弹、目标机均视为质点，忽略地球引力，并假设速度均不变。

图1 二维攻击导弹-目标机相对运动关系

根据几何关系，可得在视线上的相对速度为：

VrMT=-VMcos(γM+λMT)-VTcos(γT-λMT)

(1)

在垂直于视线上的相对速度为:

VλMT=-VMsin(γM+λMT)-VTsin(γT-λMT)

(2)

由式(1)、式(2)得到相对运动方程为:

(3)

当存在惯性环节时，定义加速度分量与控制量分量关系如下：

(4)

式中:τM表示攻击弹M的时间常数。

PN制导与APN制导的基本结构相同，可统一表达为[10]：

(5)

式中：Ni表示导弹的导航系数；Zi表示零控脱靶量；tgo表示导弹的剩余飞行时间。

当采用PN制导时，NPN在3～5之间，零控脱靶量为：

(6)

当采用APN制导时，NAPN在3～5之间，零控脱靶量为：

(7)

2 二维平面下的三体对抗策略

通常在研究物体运动的过程中，可以将空间的运动分解为互相垂直的两平面的运动并分别进行分析。因此，为研究方便，首先对二维平面主动防御策略展开研究。

攻击导弹(Attacking Missile, M)：攻击目标飞行器；防御导弹(Defender Missile, D)：拦截攻击导弹；预警机(Evading Aircraft, T)：促进拦截导弹成功摧毁攻击导弹，同时规避攻击导弹的攻击。三体对抗问题可分为2组追逃问题，即M→T追逃问题和D→M追逃问题。攻击导弹M，防御导弹D，目标机T组成的三体攻防对抗模型如图2所示。

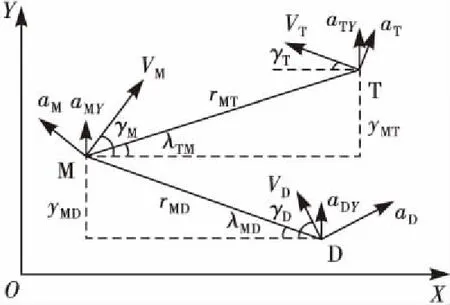
图2 T-M-D平面几何关系

图中，X轴是M→T的初始视线，xi(i=M,D,T)、yi(i=M,D,T)分别为X轴、Y轴方向的坐标；(Vi,ai,γi)为各飞行器的速度、加速度和航向角，且ai⊥Vi,i={M,D,T}；λMT,λMD为M→T,D→M的视线角；rMT,rMD为M→T,D→M的相对距离；yMT,yMD为rMT,rMD沿Y轴的分量。

目标机、攻击导弹、防御导弹均采用如下的模型统一描述[17]：

(8)

令状态向量为：

则三体攻防对抗的状态方程为：

(9)

式中：x1和xnM+nT+3为垂直于LOSO的相对位置；x2和xnM+nT+4为侧向速度，其导数为侧向加速度。上式改写为：

(10)

设rMT(0)和rMD(0)为初始距离，假设攻击导弹速度VMT和拦截导弹速度VMD为常值。攻击/拦截时间近似为tMT=rMT(0)/VMT和tMD=rMD(0)/VMD，拦截时间间隔为Δt=tMT-tMD。若拦截任务成功则Δt>0，拦截任务剩余时间和为tgo MD=tMD-t，拦截任务实际剩余时间为tgo 1=tgo MD，攻击任务实际剩余时间为tgo MT=tgo+Δt。

将攻击导弹制导律式(5)代入上述主动防御对抗系统，设计最优协同制导律。优化目标是使拦截导弹与攻击导弹的脱靶量最小并且总控制能量最小，因此构造如下目标函数：

(11)

引入零控脱靶量：

ZMD(t)=DΦ(tMD,t)x(t)

(12)

式中：Φ(tMD,t)为转移矩阵。由于其仅与拦截导弹控制率uD和飞机控制率uT有关，由此可将问题转化为：

(13)

3 三维平面下的三体对抗策略

3.1 模型描述

在实际主动防御对抗中，整个作战过程均是在三维空间中完成的。因此，对于“战斗机-攻击导弹-防御导弹”三者的对抗问题，必须在三维空间中进行研究。从理论上讲，一个三维空间运动，可以通过2个或多个二维运动分别加以描述[17]，因此本文考虑将三维空间的三体对抗过程，将其对抗轨迹分别投影到空间坐标系下两平面平面中分别研究，以图3为例，投影至和平面。

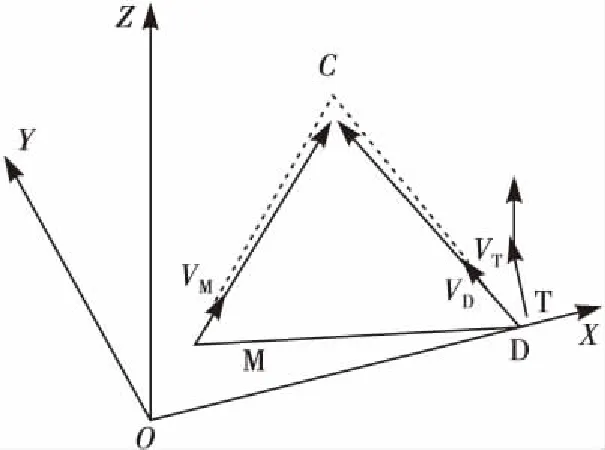
图3 T-M-D空间几何关系

式中：M(xM,yM,zM)，D(xD,yD,zD)，T(xT,yT,zT)，

VM=(cosψMcosθM,cosψMsinθM,sinψM)，

VD=(cosψDcosθD,cosψDsinθD,sinψD)，

VT=(cosψTcosθT,cosψTsinθT,sinψT)，

ψi为各飞行器的倾斜角，θi为各飞行器的方位角。仍然假设2个追逃过程均发生在初始三角碰撞区域附近，即M-D-C共面(见图4)，由此可得到VD。

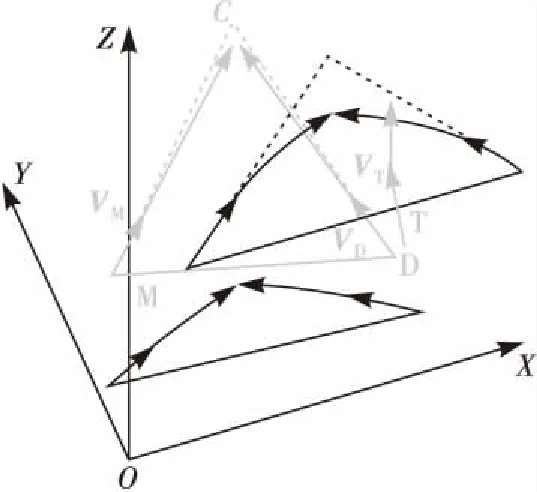
图4 T-M-D空间投影几何关系

将T-M-D由三维空间投影至XOZ平面(见图5)。

图5 XOZ平面上T-M-D平面几何关系

M1(xM,zM)，D1(xD,zD)，T1(xT,zT)，VM1=(cosψMcosθM,sinψM)VD1=(cosψDcosθD,sinψD)VT1=(cosψTcosθT,sinψT)Vi1=Vicosθi,γi1=ψi,i={M,T,D}

另外，Vi1沿X轴的分量Vi1X=Vicosθicosγi1=Vicosθicosψi；Vi1沿Z轴的分量Vi1Z=Vicosθisinγi1=Vicosθisinψi。

将T-M-D由三维空间投影至平面(见图6)。

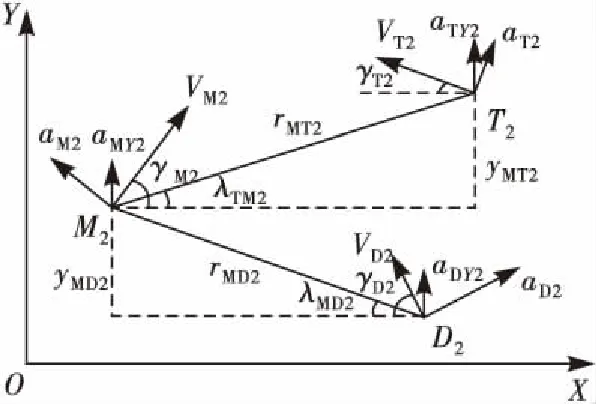
图6 XOY平面上T-M-D平面几何关系

M(xM,yM)，D(xD,yD)，T(xT,yT)VM=(cosψMcosθM,cosψMsinθM)VD=(cosψDcosθD,cosψDsinθD)VT=(cosψTcosθT,cosψTsinθT)Vi2=Vicosψi,γi2=θi,i={M,T,D}

另外，vi2x=Vicosψicosγi2=Vicosψicosθi=Vi1x；Vi2沿Y轴的分量Vi1Z=Vicosψisinγi2=Vicosψisinθi。

由此可见，两平面上速度关于公共轴的分量相等。

3.2 时间轴

在三维空间中，由XOY平面T-M-D平面几何关系可知T、M、D之间距离向量为：

(17)

(18)

速度向量与距离向量的夹角余弦值为：

因此由运动关系得到三维下T、M、D之间接近速度为：

Vclose_MD=VMcos〈VM,rMD〉+VDcos〈VD,rDM〉

(19)

Vclose_MT=VMcos〈VM,rMT〉+VTcos〈VT,rTM〉

(20)

设三维下的碰撞时间为：

(21)

(22)

在XOY平面上，攻击导弹、防御导弹、目标机的速度大小及速度航迹角为：

VM1=|VMcosψM|，VD1=|VDcosψD|，VT1=|VTcosψT|

γM1=θM，γD1=θD，γT1=θT

攻击导弹、防御导弹、目标机位置分量分别为：

XM1=XM,YM1=YM,XT1=XT,YT1=YT,XD1=XD,YD1=YD

得到攻击导弹与防御导弹、目标机的距离为：

(23)

(24)

以及M→T和M→D的视线角为：

(25)

(26)

得到二维下T、M、D之间接近速度为：

Vclose_MT1=-VM1cos(γM1-λMT1)-VT1cos(γT1+λMT1)

(27)

Vclose_MD1=-VM1cos(γM1-λMD1)-VD1cos(γD1+λMD1)

(28)

及二维下的碰撞时间为：

(29)

(30)

在XOZ平面上可知攻击导弹、防御导弹、目标机的速度大小及速度航迹角为：

(31)

(32)

(33)

(34)

(35)

(36)

攻击导弹、防御导弹、目标机在坐标轴上的位置分别为：

XM2=XM,YM2=ZM,XD2=XD,YD2=ZD,XT2=XT,YT2=ZT

得到攻击导弹与防御导弹、目标机的距离为：

M→T和M→D的视线角为：

得到二维下T、D、M之间接近速度为：

Vclose_MD2=-VM2cos(γM2+λMD2)-VD2cos(γD2-λMD2)

(37)

Vclose_MT2=-VM2cos(γM2+λMT2)-VT2cos(γT2-λMT2)

(38)

及二维下的碰撞时间为：

(39)

(40)

由投影关系可知，存在tgo=tgo 1=tgo 2，tgo MT=tgo MT1=tgo MT2。

3.3 协同制导策略

将T-M-D由三维空间投影至平面(见图7)。

图7 YOZ平面上T-M-D平面几何关系

构造如下优化问题，使得攻击导弹-拦截导弹脱靶距离|yMD(tMD)|最小。

Minimize

Subject to

(41)

其中，

(42)

令：

(43)

(44)

由此可得：

J=JXOY+JXOZ

(45)

可分解为XOY和XOZ平面独立的最优求解问题。

在XOY平面上，求解如下问题：

(46)

在XOZ平面上，求解如下问题：

(47)

3.4 问题的求解

在XOY平面上，应用拉格朗日乘子法，构造增广泛函：

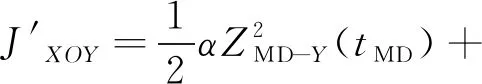
(48)

式中：λZMD-Y为待定的拉格朗日乘子系数。

构造哈密尔顿函数(Hamiltonion)：

(49)

由此可得：

(50)

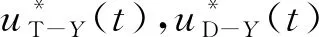
(51)

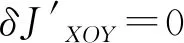
因此，由式(51)得到伴随方程：

(52)

由式(51)、式(52)得到横截条件：

λZMD-Y(tMD)=αZMD-Y(tMD)

(53)

由式(51)得到控制方程：

(54)

结合式(49)，式(52)，式(54)求解得到：

(55)

因此得到：

(56)

对式(56)积分得到：

(57)

由式(57)得到：

ΦZMD-Y(tMD,t)=

(58)

最终求得目标机和防御导弹在XOY平面上的最优制导律为：

(59)

在XOZ平面上，按照上述XOY平面上的求解过程，同理可得目标机和防御导弹在XOZ平面上的最优制导律为：

(60)

4 仿真实验

为了验证本文设计的最优协同制导律的有效性，假设在敌机发射攻击导弹之初，防御方发射防御导弹进行拦截。将主动防御导引律做为飞机-导弹协同主动防御方法中防御导弹的导引律，以飞机、防御导弹共同作为主动防御策略的实施主体，设脱靶量小于1 m做为拦截有效的指标，分析其拦截效能[17]。设仿真步长T=0.5 ms，目标机、攻击导弹及防御导弹的模型参数和初始状态分别如表1和表2所示。

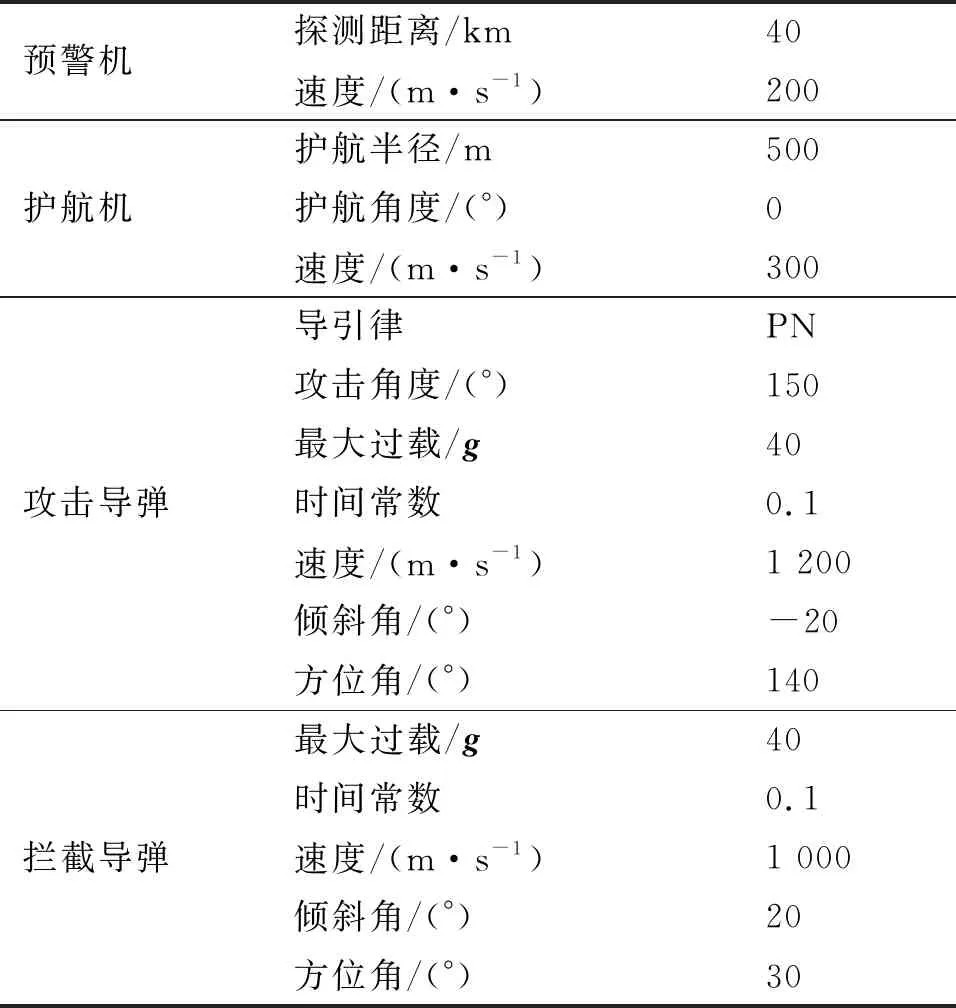
表1 One-on-One仿真系统参数

表2 目标机、防御导弹、攻击导弹初始状态

实验1采用传统的PN导引律律，仿真结果分别如图8和图9所示。

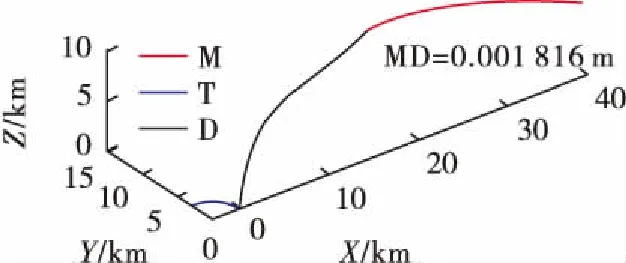
图8 拦截轨迹

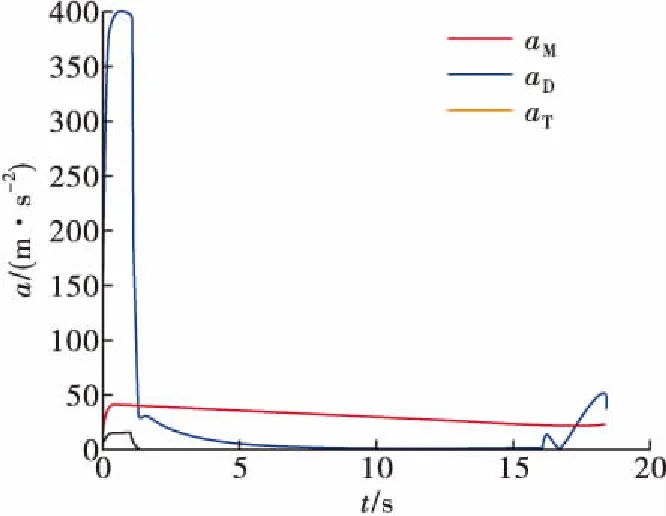
图9 加速度变化

由图8和图9可知，将目标机、防御导弹同时作为主动防御策略的实施主体，采用PN导引律时，其有效脱靶量为0.001 8 m，最大过载约40g，满足防御要求，能够实现对攻击导弹的有效拦截，由此验证了PN导引律的有效性。

在相同的初始条件下，实验2采用最优协同制导律，其仿真结果如图10和图11所示。

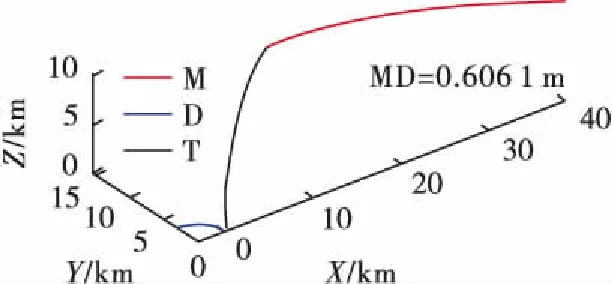
图10 拦截轨迹

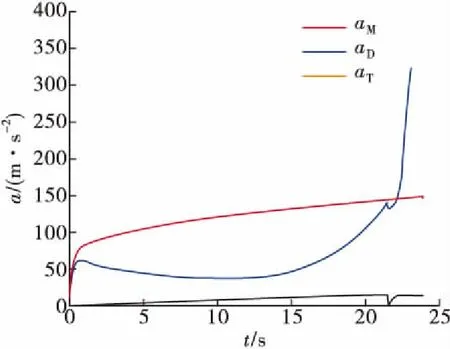
图11 加速度变化

由图10和图11可知，采用最优制导律时，能够实现对攻击导弹的有效拦截，其有效脱靶量为0.61 m，在末短时出现最大过载约35g。上述仿真同样也验证了主动防御最优协同制导律的有效性，同时由于PN制导律只需考虑脱靶量指标，因此防御导弹脱靶量精度比最优协同要高，但最优导引律下防守方能够以小于采用PN导引律所需的代价引诱并拦截攻击导弹，即采用最优协同制导律时，对防御导弹的过载要求减少，因此通过调节参数，能够协调指标平衡，这证明了最优制导律相较于PN导引律的优越性。

5 结语

本文主要在对飞机主动防御问题分析的基础上，提出了飞机-导弹协同主动防御的方法。采用最优控制理论，提出了一种基于变分法的主动防御最优协同制导律设计方法，首先在二维平面内，建立了基于LOS的三体对抗模型，结合攻击导弹、防御导弹、目标机和攻击导弹的制导律数学模型，建立各自情况下的主动防御系统运动方程；综合考虑拦截脱靶量、控制量等优化指标，进一步将主动防御制导律设计问题转化为最优控制问题，采用变分法，根据最优化的条件，推导出了二维平面内目标机与拦截导弹协同的最优主动防御制导律。在此基础上，通过三维空间主动防御过程的二维投影的方法，将三维主动防御制导律设计问题转化为两个相互约束的二维平面制导律(水平面和垂直面)设计问题，实现了协同制导律从二维平面向三维空间的扩展，提高实战应用效果。