平面平行运动的刚体弹性碰撞问题的探讨
2020-07-01陈铁松
陈铁松
(长春吉大附中实验学校 吉林 长春 130021)
在研究碰撞问题中,引入恢复系数后,恢复系数成为求解碰撞问题的关键参数之一. 许多教材中关于恢复系数的引入情景都类似,即在光滑水平面上可以看成质点的自由二体碰撞过程中,给出恢复系数的定义.对于弹性碰撞过程,由动量守恒和动能不变可求得碰撞前后两个质点的相对速度大小相等,即恢复系数等于1. 对于不可看作质点的做平面平行运动的刚体发生弹性碰撞,碰撞前后碰撞点沿碰撞力方向的相对速度大小相等是否还适用,教材中都没有明确指出这一点,导致学生对弹性碰撞问题的规律认识不够深入,求解问题时考虑不够全面或陷入复杂的数学运算.
本文证明了两个做平面平行运动的刚体发生弹性碰撞过程中,发生碰撞的两点在碰撞力的方向上相对速度大小相等,这个结论与碰撞前后系统动能不变是等价的,并用此结论求解一道物理竞赛题目,很容易得出结果.
1 两个不可看作质点的刚体发生弹性碰撞
如图1所示,表面呈几何光滑的两个刚体在光滑的水平面上运动,参考系选择为地面.某时刻两个刚体发生弹性碰撞.设刚体1的质量为m1,绕质心运动的转动惯量为J1,质心初速度大小为v10,初始角速度大小为ω10,刚体2的质量为m2,绕质心运动的转动惯量为J2,质心初速度大小为v20,初始角速度大小为ω20;碰撞后刚体1的质心速度大小为v1,角速度大小为ω1,刚体2的质心速度大小为v2,角速度大小为ω2,各个矢量的方向如图1标注所示.为了数学处理简单且不失一般性质,我们假设两个刚体质心的初速度方向相反,且碰撞点的法线方向与它们各自的质心初速度方向相同.

图1 两个不可看作质点的刚体发生弹性碰撞
假设碰撞过程中,两个刚体间的冲量大小为I,由动量守恒
-I=m1v1-m1v10I=m2v2-(-m2v20)
(1)
对刚体质心的冲量矩定理
Ir1=J1ω1-J1ω10Ir2=J2ω2-(-J2ω20)
(2)
两个刚体弹性碰撞,接近速度等于远离速度
v10-ω10r1-(-v20-ω20r2)=
v2+ω2r2-(v1-ω1r1)
(3)
由式(1)、(2)、(3)解得
碰撞后两个刚体的总动能
(-Ir1ω10+Ir2ω20+Iv10+Iv20)]
代入I的表达式后得
(-Ir1ω10+Ir2ω20+Iv10+Iv20)=0
即弹性碰撞前后,两个刚体系统的总动能保持不变.
2 结论的应用
【题目】由绝对刚性的轻杆连接两个很小的重球组成“哑铃”,以速度v0沿垂直于静止不动的光滑墙面平动,并且“哑铃”的轴与墙面成45°角,如图2所示.问当“哑铃”与墙面发生弹性碰撞后将怎样运动?
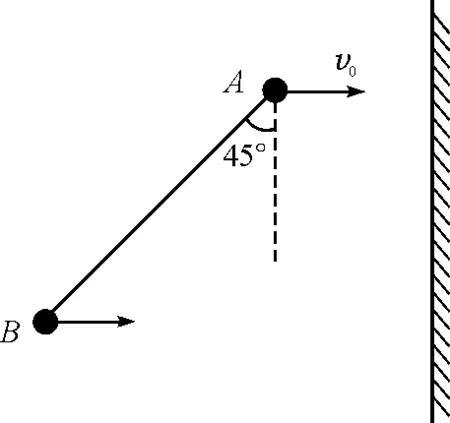
图2 题目情境图
这是一道关于碰撞的竞赛题,题目的情景对学生来说非常的熟悉,解题切入点也很容易找到.球A与墙壁发生弹性碰撞过程,由于有轻杆的束缚作用,不能简单地把球A看成质点,所以大多数学生都是采用动量守恒和能量守恒相结合的方式完成题目的求解,参考书中也是采用这个思路求解的.但是采用这种方法求解不可避免地要去求解二次方程,计算量会比较大.下面应用刚体弹性碰撞中碰撞点的恢复系数为1的结论结合“哑铃”系统碰撞前后角动量守恒求解本题.
设球A与墙壁发生碰撞后,“哑铃”系统质心的速度大小为v1,两球绕质心转动的角速度为ω,应用本文结论,球A与墙壁发生弹性碰撞,碰撞点恢复系数为1,即分离速度大小等于接近速度大小
对“哑铃”系统由角动量守恒得
以上两式子联立解得
3 总结
利用动量守恒和角动量定理,并结合弹性碰撞过程中碰撞点在碰撞力的方向上碰撞前后相对速度的大小相等,即恢复系数等于1这个结论,推导得出弹性碰撞前后,两个刚体系统的总动能保持不变.上述分析中,平面平行运动的刚体的速度方向、角速度方向的假设具有任意性,所以这个结论在刚体平面平行运动的碰撞过程中是普遍成立的,该结论在处理平面平行运动刚体的弹性碰撞问题时具有一定的参考价值.
